stanford的course note 近日在维护中,所以换了http://cs231n.stanford.edu/slides/网页的lecture4作为最优化部分的学习资料。
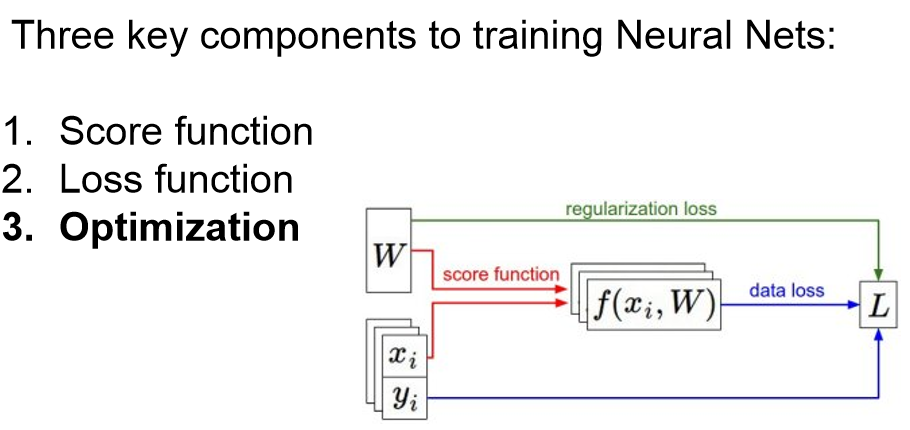
训练神经网络的三要素是:
1. 确定判别函数
2. 确定损失函数
3. 最优化
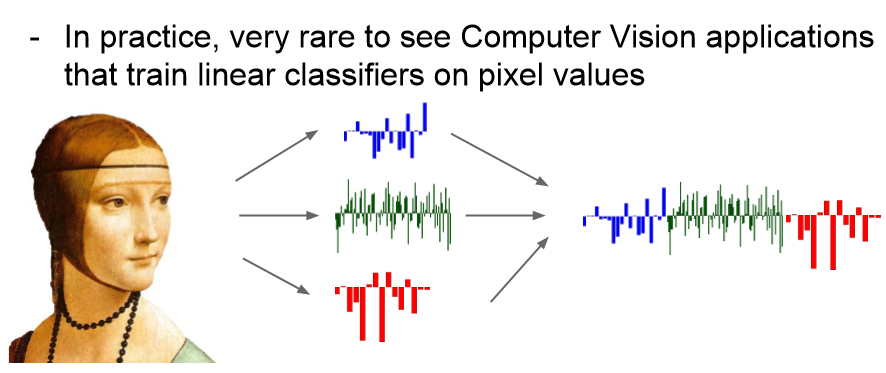
实践中很少用像素的取值去直接训练神经网络。
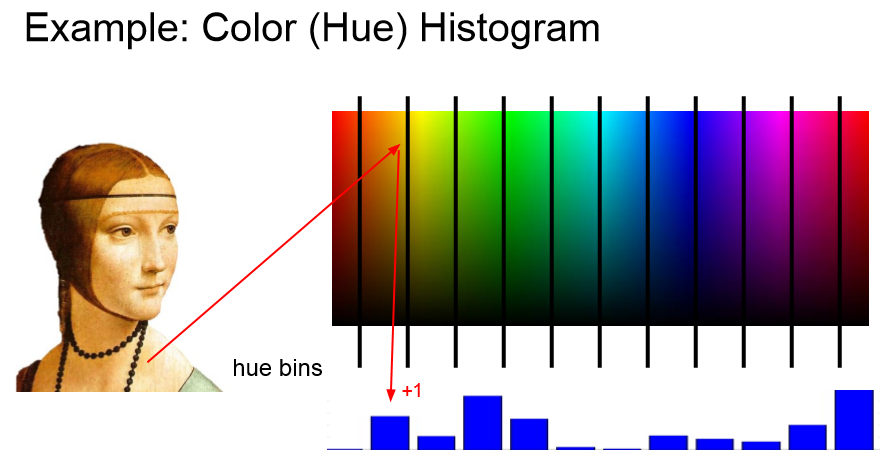
我们采用的是图像的特征,例如:直方图、HOG特征、 Bag of Words
HOG提取算法:每次扫描图像的一块8*8的小区域,获取边缘方向。一共有9中方向。
将图片块的大小调整为32*32,在每个调整后的图片块(patch)上采用HOG算法。

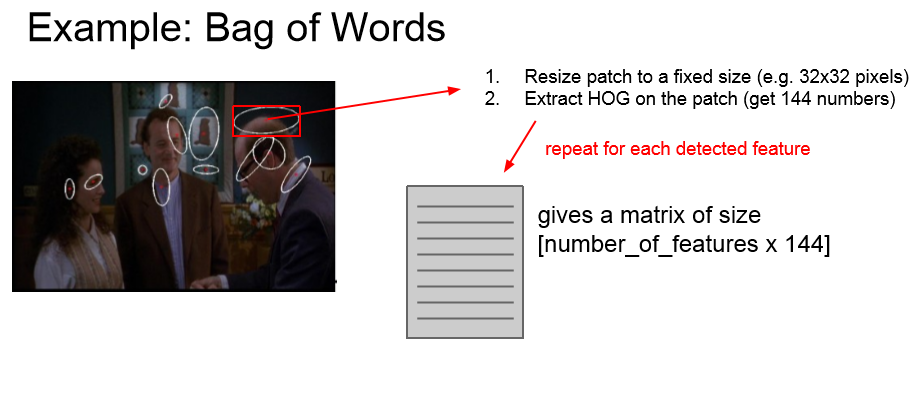
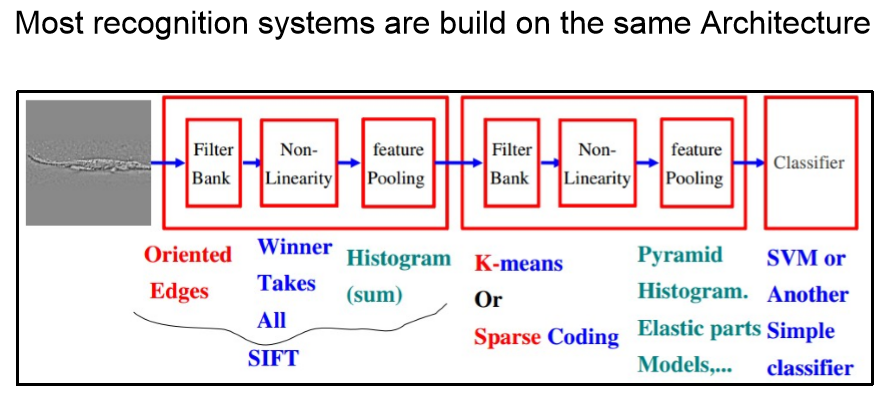
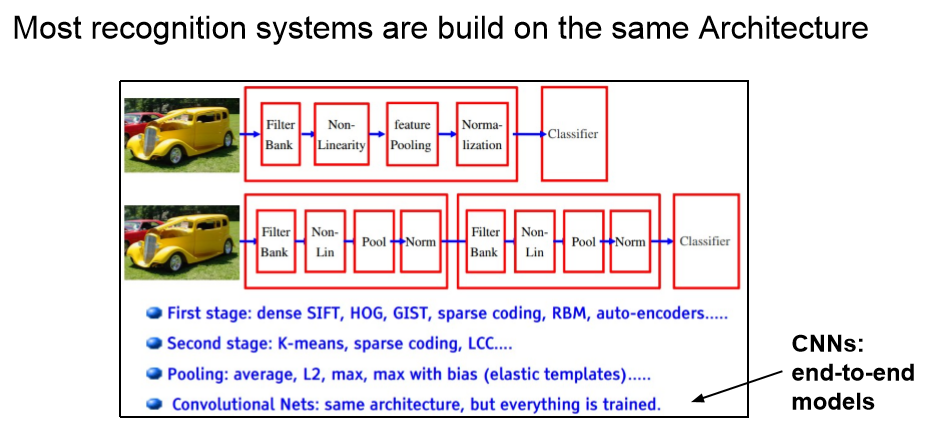
绝大多数感知系统都采用下面这种结构:
损失函数可视化
最优化的目的就是要找到损失函数取最小值时,W的取值。如果我们能将损失函数可视化,找最小值就是轻而易举的。但是,损失函数中包含高维向量W,将高维空间可视化的难度很大,所以首先我们需要采用某些方法来“降维”。
回顾一下,SVM的损失函数:
不同取值W的L的值可以看作是超平面中的一个点,当然这个超平面是高维空间。如果我们选择某一个特定的方向,这个方向用向量W1来表示。W1是一维的,可以用数组表示,它可以看作是超平面中的一个固定的点。新的损失函数就是原损失函数与这个固定点的差值。
重新定义改写一下损失函数:
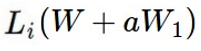
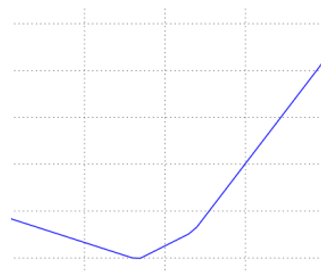
α是一个可变参数。将α作为x轴自变量,新的损失函数作为y轴应变量。画图:
我们可以很容易找出改写后的损失函数的最小值以及此时所对应的α。
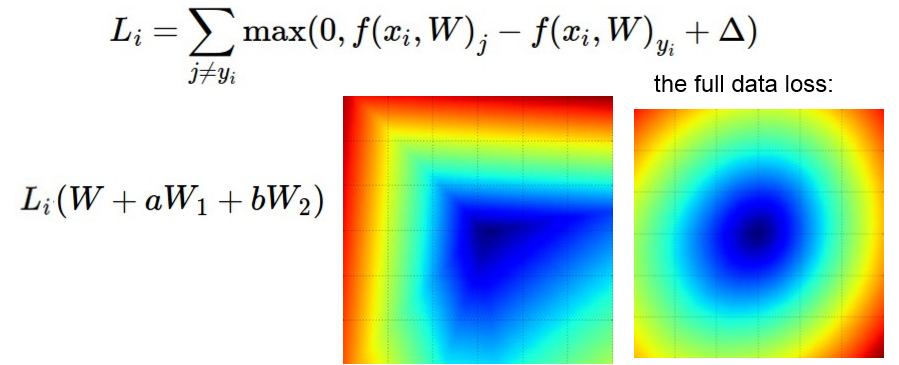
同样,我们也可以用原损失函数减去两个向量W1,W2。a,b分别对应x轴和y轴,新的损失函数可以用类似等高线的方式用颜色来表示。蓝色部分对应的损失函数取值低,红色部分取值高。
对于一个具体的样本,损失函数的计算式如下所示:
这个式子的取值可能是正的(错误分类时),也可能是负的(正确分类时)
假设现在有一个简单的训练集,包含三种类别的图像(每个类别的样本各一个),因此需要三种判别函数,W中会包含3行,对应的用不同下标表示。
对于每一个样本,要考虑单个的损失函数。整个SVM的损失函数是三个样本的损失函数情况取平均:
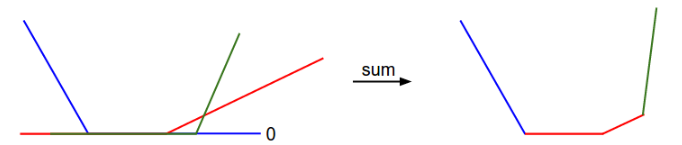
绘图之后的样子:
从上图可以看出,SVM的损失函数是凸函数,可以用凸函数求解最优化的一系列方法来求取最优解。但是在神经网络中,损失函数并不是凸函数,情况会复杂许多。另外,从SVM损失函数的表达式来看,此函数并不是可微的。但是次梯度法( subgradient )仍旧是有效可用的。后面会有实际的例子。
最优化
最优化的目的是寻找最合适的W使得损失函数取值最小。
方法一:随机寻找W,作比较,直到找到最合适的。这种方法是“暴力破解”,并不推荐。
方法二:首先随机确定W,再通过迭代,每一次都寻找一个更合适的W。 这种方法的准确率达到21.4%。因为很多这种方法时间复杂度高,而且其中有很多计算并不是必须的,是存在浪费的。所以人就不推荐。
方法三:沿着梯度的方向搜索。想象一下,如果你在山上,想要最快速度的下山,是不是应该选择最陡峭的一条路而不是缓缓地盘山路。损失函数可视化之后可以看作是一座山,无论我们选取的初值W在山上的那个位置,我们的目标都是要去山脚(损失函数取得最小值的点)。所以现在我们要找到那条最陡峭的下山路,这条路就是梯度的方向。一维变量中,梯度的定义如下:
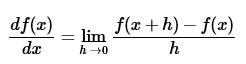
计算梯度有两种算法:一种简单但是比较慢,另一种比较快但是有较高的错误率,需要用算法修正。下例给出简单的梯度算法:
首先定义每一个样本的损失函数L_i_vectorized(x, y, W)
def L_i_vectorized(x, y, W):
"""
A faster half-vectorized implementation. half-vectorized
refers to the fact that for a single example the implementation contains
no for loops, but there is still one loop over the examples (outside this function)
"""
delta = 1.0
scores = W.dot(x)
# compute the margins for all classes in one vector operation
margins = np.maximum(0, scores - scores[y] + delta)
# on y-th position scores[y] - scores[y] canceled and gave delta. We want
# to ignore the y-th position and only consider margin on max wrong class
margins[y] = 0
loss_i = np.sum(margins)
return loss_i
然后计算所有训练集样本的总的损失函数的平均值。
def L(X, Y, W):
"""
fully-vectorized implementation :
- X holds all the training examples as columns (e.g. 3073 x 50,000 in CIFAR-10)
- y is array of integers specifying correct class (e.g. 50,000-D array)
- W are weights (e.g. 10 x 3073)
"""
Loss_sum=0
for i in range(50000):
x=X[i]
x=np.append(x,1)
y=Y[i]
loss_i=L_i_vectorized(x, y, W)
#print loss_i
#print "#####################"
Loss_sum+=loss_i
#print Loss_sum
L=Loss_sum/50000
#print i
#print "L="
#print L
#print "#####################"
return L
def CIFAR10_loss_fun(W):
return L(Xtr, Ytr, W)计算梯度
def eval_numerical_gradient(f, x):
"""
a naive implementation of numerical gradient of f at x
- f should be a function that takes a single argument
- x is the point (numpy array) to evaluate the gradient at
"""
fx = f(x) # evaluate function value at original point
grad = np.zeros(x.shape)
h = 0.00001
# iterate over all indexes in x
it = np.nditer(x, flags=['multi_index'], op_flags=['readwrite'])
while not it.finished:
# evaluate function at x+h
ix = it.multi_index
old_value = x[ix]
x[ix] = old_value + h # increment by h
fxh = f(x) # evalute f(x + h)
x[ix] = old_value # restore to previous value (very important!)
# compute the partial derivative
grad[ix] = (fxh - fx) / h # the slope
it.iternext() # step to next dimension
return grad调整,找到最合适的步长(step)
W = np.random.rand(10, 3073) * 0.001 # random weight vector
df = eval_numerical_gradient(CIFAR10_loss_fun, W) # get the gradient
loss_original = CIFAR10_loss_fun(W) # the original loss
print 'original loss: %f' % (loss_original, )
# lets see the effect of multiple step sizes
for step_size_log in [-10, -9, -8, -7, -6, -5,-4,-3,-2,-1]:
step_size = 10 ** step_size_log
W_new = W - step_size * df # new position in the weight space
loss_new = CIFAR10_loss_fun(W_new)
print 'for step size %f new loss: %f' % (step_size, loss_new) 上述程序运行之后,可以看出,在step选择为6的时候,损失函数最小。这就引出了在神经网络算法中最终要的参数选取问题————step的大小。step如果选的过小,整个运算会消耗很长时间。如果选的过大,运算过程会加速,但是有点冒险。其中细节将在以后讨论。
在上例中我们采用的是简单的numerical gradient 来求取梯度,这种算法非常简单但是计算复杂度大,消耗很多计算资源。另外一种更高效的算法是使用微积分( Calculus )来计算梯度。这种算法更快速高效,但是错误率高。在实践中,我们经常通过比较 Calculus和numerical gradient 来修正Calculus计算出的梯度。这个过程被称作“梯度矫正”。
以SVM为例,若采用Calculus来计算梯度,我们使用下面的式子:
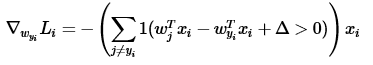
定义了梯度之后,就可以采用梯度下降算法来搜做最优解:
while True:
weights_grad = evaluate_gradient(loss_fun, data, weights)
weights += - step_size * weights_grad # perform parameter update
梯度搜索算法是适用范围最广的神经网络损失函数最优化算法。但是对于容量较大的数据集,计算出全部的损失函数非常费时费力。计算成本太高,因此,我们可以采取Mini-batch 的方法,每次取出训练集中的一部分样本作为batch,用batch来计算和调整参数。例如,每次选取256个样本作为一个batch:
while True:
data_batch = sample_training_data(data, 256) # sample 256 examples
weights_grad = evaluate_gradient(loss_fun, data_batch, weights)
weights += - step_size * weights_grad # perform parameter update小的batch计算出的损失函数,是整个样本集损失函数的近似。Mini-batch的极端情况是每个batch只含有单个样本。这种情况被称为Stochastic Gradient Descent (SGD),实践中并不常见,因为在实践中,计算100个样本的损失函数比计算1个样本的损失函数100次的计算效率更高。batch的大小是一个超参数,但是我们很少用交叉验证的方式来求取最优值。经常采用一些设定的值,如32,64,128等。










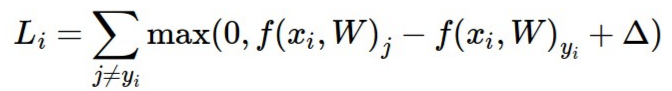
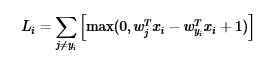
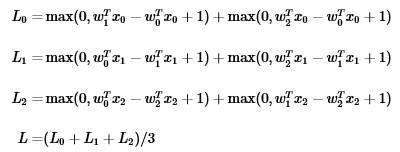















 8882
8882

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?










