运动学与动力学约束下的在线机器人时间最优轨迹规划算法(Topp-RA)

关键词： 轨迹规划、时间最优、动力学约束、机器人、在线
KeyWord:Trjectory plan、Time-Optimal、Dynamics constraint、Robot、Online

一、简介

1.1 问题描述

对于机器人来说，轨迹规划通常可以分为两个层次，第一个层次，根据碰撞等约束找到空间中的几何路径点，不带时间信息，通常称之为路径规划(path planning)，该问题的求解思路可以参考这里，第二个层次是根据已经获取的路径以及机器人系统的约束，找到一条带时间参数的轨迹(trajectory planning)，本文章的就是尝试去解决第二个问题。
对于机器人来说，时间最优的轨迹规划在一些的场景下是非常有意义的事情，比如抓取，通常希望节拍越快越好，大多数的轨迹规划约束通常只考虑机器人的运动学约束，但在很多时候，机器人在达到运动学约束时，驱动器的能力并没有拉满，因此时间最优的轨迹规划考虑动力学约束是非常有意义的，这篇文章就是以时间最优为目标，考虑动力学约束进行轨迹规划。

1.2 时间最优轨迹规划现状简介

当前动力学约束下的时间最优的轨迹规划思路主要有两类，第一类是基于数值积分的方法【Numerical Integration (NI)】，类似bang-bang控制的思路，该方法求解时间快，有利于进行在线求解，但是很难求解，鲁棒性不足；第二类方法是基于凸优化的方法【Convex Optimization(CO)】，该方法问题很好形成，只要形成凸优化问题，即可找到现有的凸优化求解器进行求解，鲁棒性也很好，但是求解效率很低，很难进行在线的轨迹规划。
当前基于CO的方法比较好的有这个库，对应文章：Time-Optimal Path Tracking for Robots a Convex Optimization Approach，这个库展示了如何形成一个凸锥问题然后进行求解的过程，原理清晰，但是求解效率很低，无法进行在线规划；基于NI的方法比较好的是Toppra库，该链接里面有对应的文章，该方法最大的缺点是不是jerk bound，因此需要考虑动力学约束，但是该库并没有展示完整的例子，这也是本文主要做的事情。

二、动力学约束下的时间最优轨迹规划

2.1 引用的库

1、Pinocchio库，动力学计算的库

几种安装方式都不是很好用，还是推荐使用conda安装。

2、Toppra库

pip install toppra

3、机器人模型库（获取urdf文件）
这个库里面包含了多种机器人模型，比如panda、UR、人形机器人等，获取机器人模型文件可以从这两获取。

2.2 相关代码

相关代码的解释在代码注释里面

import toppra as ta
import pinocchio
import numpy as np
import time
import matplotlib.pyplot as plt

def generate_random_trajectory(robot, npts, maxd, randskip=0):
    for i in range(randskip):
        pinocchio.randomConfiguration(robot)    
    ts = [
        0.0,
    ]
    qs = [
        pinocchio.randomConfiguration(robot),
    ]
    while len(qs) < npts:
        qlast = qs[-1]
        q = pinocchio.randomConfiguration(robot)
        d = pinocchio.distance(robot, qlast, q)
        if d > maxd:
            q = pinocchio.interpolate(robot, qlast, q, maxd / d)
        qs.append(q)
        ts.append(ts[-1] + pinocchio.distance(robot, qlast, q))
    # Compute velocities and accelerations
    vs = [
        np.zeros(robot.nv),
    ]
    accs = [
        np.zeros(robot.nv),
    ]
    eps = 0.01
    for q0, q1, q2 in zip(qs, qs[1:], qs[2:]):
        qprev = pinocchio.interpolate(
            robot, q0, q1, 1 - eps / pinocchio.distance(robot, q0, q1)
        )
        qnext = pinocchio.interpolate(
            robot, q1, q2, eps / pinocchio.distance(robot, q1, q2)
        )
        # (qnext - qprev) / eps
        vs.append(pinocchio.difference(robot, qprev, qnext) / eps)
        # ((qnext - q) - (q - qprev)) / eps^2
        accs.append(
            (
                pinocchio.difference(robot, q, qnext)
                - pinocchio.difference(robot, qprev, q)
            )
            / (eps ** 2)
        )
    vs.append(np.zeros(robot.nv))
    accs.append(np.zeros(robot.nv))  
    path = ta.SplineInterpolator(np.linspace(0, 1, npts), qs) #采用Spline进行path的插值
    return path
    
def joint_velocity_constraint(robot, scale=1.0):
    from toppra.constraint import JointVelocityConstraint
    return JointVelocityConstraint(
        np.vstack(
            [-scale * robot.velocityLimit, scale * robot.velocityLimit]
        ).T
    )    
    
def joint_acceleration_constraint(robot, limit):
    from toppra.constraint import JointAccelerationConstraint, DiscretizationType
    l = np.array([limit,] * robot.nv)
    ja = JointAccelerationConstraint(np.vstack([-l, l]).T)
    ja.discretization_type = DiscretizationType.Interpolation
    return ja

def inv_dyn1(robot,q, v, a):
        data = robot.createData()
        return pinocchio.rnea(robot,data, q, v, a)
    
def torque_constraint(robot, scale=1.0):
    from toppra.constraint import JointTorqueConstraint, DiscretizationType
    def inv_dyn(q, v, a):
        data = robot.createData()
        return pinocchio.rnea(robot,data, q, v, a)

    jt = JointTorqueConstraint(
        inv_dyn,
        np.vstack(
            [-scale * robot.effortLimit, scale * robot.effortLimit]
        ).T,
        np.zeros(robot.nv),
    )
    jt.discretization_type = DiscretizationType.Interpolation
    return jt    
    
def main():
    robot = pinocchio.buildModelFromUrdf('robot.urdf') #导入机器人模型
    print('robot name: ' + robot.name)
    path = generate_random_trajectory(robot, 5, 0.3)#生成路径规划点
    constraints = [
        joint_velocity_constraint(robot),#速度约束
        joint_acceleration_constraint(robot, 2.0),#加速度约束
        torque_constraint(robot),#动力学约束
    ]
    
    Ngripoints = 1000
    instance = ta.algorithm.TOPPRA(
        constraints,
        path,
        solver_wrapper="seidel",
        gridpoints=np.linspace(0, path.duration, Ngripoints + 1)
    )#构建TOPPRA问题
    jnt_traj = instance.compute_trajectory(0, 0)
    ts_sample = np.linspace(0, jnt_traj.get_duration(), 100)
    print("traj duration:",jnt_traj.get_duration())#输出轨迹的耗时
    
    #轨迹的位置、速度、加速度信息
    qs_sample = jnt_traj.eval(ts_sample)
    qds_sample = jnt_traj.evald(ts_sample)
    qdds_sample = jnt_traj.evaldd(ts_sample)

	#计算输出轨迹的力矩信息
    torque = []
    for q_, qd_, qdd_ in zip(qs_sample, qds_sample, qdds_sample):
        torque.append(inv_dyn1(robot,q_, qd_, qdd_))
    torque = np.array(torque)

	#绘制力矩
    fig, axs = plt.subplots(6, 1)
    for i in range(0, 6):
        axs[i].plot(ts_sample, torque[:, i])
    plt.xlabel("Time (s)")
    plt.ylabel("Torque $(Nm)$")
    plt.legend(loc='upper right')
    plt.show()       
    
    #绘制位置
    fig, axs = plt.subplots(6, 1)
    for i in range(0, 6):
        axs[i].plot(ts_sample, qs_sample[:,i],label = "pos")
        axs[i].legend()
    plt.show()   
 
 	#绘制速度
    fig, axs = plt.subplots(6, 1)
    for i in range(0, 6):
        axs[i].plot(ts_sample, qds_sample[:,i],label = "vel")
        axs[i].legend()
    plt.show()  
    
	#绘制加速度
    fig, axs = plt.subplots(6, 1)
    for i in range(0, 6):
        axs[i].plot(ts_sample, qdds_sample[:,i],label = "acc")
        axs[i].legend()
    plt.show()          

    # Compute the feasible sets and the controllable sets for viewing.
    # Note that these steps are not necessary.
    _, sd_vec, _ = instance.compute_parameterization(0, 0)
    X = instance.compute_feasible_sets()
    K = instance.compute_controllable_sets(0, 0)

    X = np.sqrt(X)
    K = np.sqrt(K)

    plt.plot(X[:, 0], c='green', label="Feasible sets")
    plt.plot(X[:, 1], c='green')
    plt.plot(K[:, 0], '--', c='red', label="Controllable sets")
    plt.plot(K[:, 1], '--', c='red')
    plt.plot(sd_vec, label="Velocity profile")
    plt.title("Path-position path-velocity plot")
    plt.xlabel("Path position")
    plt.ylabel("Path velocity square")
    plt.legend()
    plt.tight_layout()
    plt.show()    
   
if __name__ == "__main__":
    main()

C++版，这里仅给出部分核心代码

  const std::string urdf_filename =  "/robot.urdf";
  pinocchio::Model model;
  pinocchio::urdf::buildModel(urdf_filename, model);
  pinocchio::Data data(model);

  auto jntTorqueCnt_ptr = std::make_shared<toppra::constraint::jointTorque::Pinocchio<>>(model);

  toppra::LinearConstraintPtrs constraints = toppra::LinearConstraintPtrs{
      std::make_shared<toppra::constraint::LinearJointVelocity>(velLimitLower, velLimitUpper),
      std::make_shared<toppra::constraint::LinearJointAcceleration>(accLimitLower, accLimitUpper),
      jntTorqueCnt_ptr};//velLimitLower，accLimitLower均为Eigen::VectorXd

  toppra::Vectors positions;//此处省略了定义positions的具体实现，需要自己定义

  std::array<toppra::BoundaryCond, 2> boundary_cond;
  toppra::BoundaryCond bc{"clamped"};

  boundary_cond[0] = bc;
  boundary_cond[1] = bc;

  toppra::Vector times(positions.size());
  times.setLinSpaced(0, 1);

  toppra::PiecewisePolyPath path =
      toppra::PiecewisePolyPath::CubicSpline(positions, times, boundary_cond);

  toppra::GeometricPathPtr path_ptr = std::make_shared<toppra::PiecewisePolyPath>(path);

  toppra::algorithm::TOPPRA problem{constraints, path_ptr};
  toppra::ReturnCode ret_code = problem.computePathParametrization();

  toppra::Vector gridpoints = problem.getParameterizationData().gridpoints;
  toppra::Vector vsquared = problem.getParameterizationData().parametrization;

  toppra::parametrizer::ConstAccel output_traj{path_ptr,
                                               problem.getParameterizationData().gridpoints,
                                               problem.getParameterizationData().parametrization};

  auto path_interval = output_traj.pathInterval();
  double duration = path_interval[1] - path_interval[0];
  std::cout << "Traj duration:" << duration << std::endl;
  int rows = std::ceil(duration / 0.002);

  toppra::Vector time(rows);
  time.setLinSpaced(0, duration);
  //插值后的位置、速度、加速度
  toppra::Vectors topp_pos_vec_ = output_traj.eval(time, 0);
  toppra::Vectors topp_vel_vec_ = output_traj.eval(time, 1);
  toppra::Vectors topp_acc_vec_ = output_traj.eval(time, 2);

2.3 效果展示

这里使用的是UR5机械臂，力矩、位置、速度、加速度曲线如下所示：




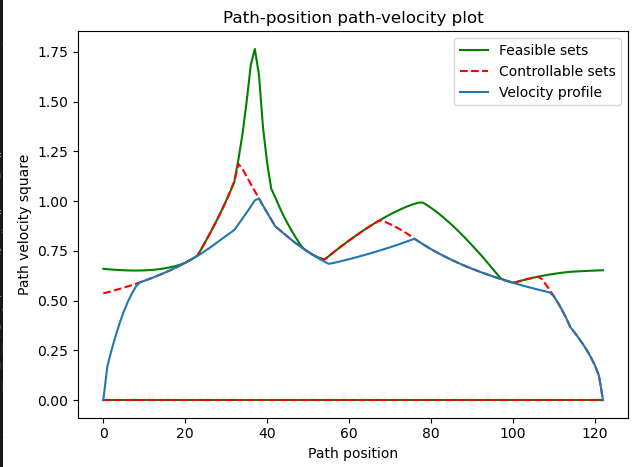
Toppra库的前向与反向传播图如下：

2.4 小结

以上代码展示了一个简单的python例子，用于时间最优的考虑动力学约束的轨迹规划，后续会推出该库的原理解析。

三、原理解析

Topp-RA库论文全名为：A New Approach to Time-Optimal Path Parameterization Based on Reachability Analysis
github地址

3.1 文章摘要以及主要贡献

我们先来看看摘要：

摘要——时间最优路径参数化 (TOPP) 是机器人技术中一个研究得很好的问题，具有广泛的应用。解决 TOPP 的方法主要有两种：数值积分 (NI) 和凸优化 (CO)。基于 NI 的方法速度快但难以实现，并且存在鲁棒性问题，而基于 CO 的方法更鲁棒，但同时速度明显较慢。在这里，我们提出了一种基于可达性分析的 TOPP 新方法。关键点是通过求解小型LP递归问题，计算路径上离散位置的可达和可控集。经过广泛的数值评估，所得到的算法比基于 NI 的方法更快，并且与基于 CO 的方法一样鲁棒（成功率为 100%）。此外，所提出的方法还提供了独特的额外好处：可以以简单自然的方式从中得出可接受的速度传播和对参数不确定性的鲁棒性。

摘要的机器翻译如上，关键部分做了加粗处理，文章提出了一种基于可达性分析的 TOPP 新方法，该方法通过求解小型LP递归问题，计算路径上离散位置的可达和可控集。该方法具有效率高，鲁棒性强的特点。

3.2 主要内容

3.2.1 整体流程

Topp-RA的求解过程主要分为两个大的步骤，首先是后向传播（bw)，如图所示，从最后一个点开始，往前进行搜索，往前搜索时会搜索出上界与下界，如图红色的竖条所示，竖条的顶部的连线即为上界限，竖条的底部连线即为下界；确定好上下界后，从起始点开始，进行前向传播，如图蓝色线条所示，前向传播选择的点都在上下界内，直到搜索到最后一个点为止。

3.2.2 问题的形成

这部分对应文章第二章，我们在上一小节已经介绍了前向传播和后向传播的概念，这里我们来看看这两个传播具体做了什么。
我们想要求解的问题是，给定一系列空间点，包含起点、终点，中间点（点数大于等于0），在机器人速度、加速度、动力学的约束下，求解时间最优的轨迹。
首先，我们把轨迹q(t)，分解成几何路径q(s)和标量s(t)（这里对应文章标题的Path Parameterization），s的范围是[0,T]，q(s)只和几何路径有关，和时间参数无关，q(s)由给定的一系列空间点进行构建得到，topp-ra库中使用的是cubic-spline（三次多项式），这样，只需要求解s(t)，就可以得到问题的解，原文如下。

然后，q(t)进行微分，得到以下的公式(2)，这里即可得到速度约束和加速度约束：

轨迹总的时间，公式如下所示，公式中的$\sqrt{x}$即为$\dot{s}$，

动力学约束写作如下形式：

然后把动力学改写一下，得到动力学约束如(5)所示，

这样，我们就形成了速度、加速度、动力学约束，我们仔细观察一下，把速度约束两边取平方以后，这三个约束正好可以形成关于${\dot{s}}^2$和$\ddot{s}$的线性组合。

3.2.3 问题的求解

这篇文章最妙的地方在于把大的复杂的优化问题分解成一系列小的简单的问题，具体如下：
我们把s(t)分成N份，如果每一份都能使得${\dot{s}}^2$最大，这样就可以使得时间最短（参考轨迹总的时间求解公式）。
这样，问题转化为求解N个小的优化问题，优化目标为${\dot{s}}^2$最大，约束为速度、加速度、动力学约束，由于三个约束正好可以形成关于${\dot{s}}^2$和$\ddot{s}$的线性组合，优化问题为LP问题。
LP问题格式如下：

两个小的问题之间的优化变量关系如下，这里的$x_i$为${\dot{s}}^2$，$\Delta$为$\ddot{s}$：

TOPP-RA算法如下图所示，这里我们回到之前提到的后向传播和前向传播（这两个传播过程就是文章标题的Reachability Analysis），后向传播搜索出上界（N个）和下界（N个），每个搜索步骤都是上面提到的小的LP问题，这样，后向传播一共需求解2N个LP问题；同样的，前向传播每次求解也是一个小的LP问题；所以，整个LP问题需要求解3N个LP问题。这样，通过前向后后向的一系列LP问题求解，即可完成轨迹的求解。

3.3 小结

其实这篇文章写的有点晦涩难懂，很多公式没有写的很清楚，需要一些基础知识，才能理解，强烈推荐结合C++代码去理解文章。
这篇文章提出的方法是开创性的，由于把复杂问题分解，很好的解决了传统方法的计算效率问题，且鲁棒性很好，但该文章并没有解决三次微分约束的问题。
由于本人水平有限，还请各位大佬指正。