各类激活函数Activation Functions介绍及实现与优缺点分析

最新推荐文章于 2024-04-10 11:32:19 发布

Fighting_1997

最新推荐文章于 2024-04-10 11:32:19 发布

阅读量2.7k

点赞数 1

分类专栏：神经网络 Python 文章标签：深度学习

本文链接：https://blog.csdn.net/frighting_ing/article/details/121590808

版权

Python 同时被 2 个专栏收录

82 篇文章 13 订阅

订阅专栏

神经网络

30 篇文章 4 订阅

订阅专栏

什么是激活函数？

激活函数（Activation functions）对于神经网络模型学习与理解复杂和非线性的函数来说具有十分重要的作用。它们将非线性特性引入到我们的网络中。

如果网络中不使用激活函数，网络每一层的输出都是上层输入的线性组合，无论神经网络有多少层，输出都是输入的线性组合。

如果使用的话，激活函数给神经元引入了非线性因素，使得神经网络可以任意逼近任何非线性函数，此时神经网络就可以应用到各类非线性场景当中了。

常见的激活函数如sigmoid、tanh、relu等，它们的输入输出映射均为非线性，这样才可以给网络赋予非线性逼近能力。

为什么需要激活函数？

（1）非线性：即导数不是常数。这个条件是多层神经网络的基础，保证多层网络不退化成单层线性网络。这也是激活函数的意义所在。

（2）几乎处处可微：可微性保证了在优化中梯度的可计算性。传统的激活函数如sigmoid等满足处处可微。对于分段线性函数比如ReLU，只满足几乎处处可微（即仅在有限个点处不可微）。对于SGD算法来说，由于几乎不可能收敛到梯度接近零的位置，有限的不可微点对于优化结果不会有很大影响[1]。

（3）计算简单：非线性函数有很多。极端的说，一个多层神经网络也可以作为一个非线性函数，类似于Network In Network[2]中把它当做卷积操作的做法。但激活函数在神经网络前向的计算次数与神经元的个数成正比，因此简单的非线性函数自然更适合用作激活函数。这也是ReLU之流比其它使用Exp等操作的激活函数更受欢迎的其中一个原因。

（4）非饱和性（saturation）：饱和指的是在某些区间梯度接近于零（即梯度消失），使得参数无法继续更新的问题。最经典的例子是Sigmoid，它的导数在x为比较大的正值和比较小的负值时都会接近于0。更极端的例子是阶跃函数，由于它在几乎所有位置的梯度都为0，因此处处饱和，无法作为激活函数。ReLU在x>0时导数恒为1，因此对于再大的正值也不会饱和。但同时对于x<0，其梯度恒为0，这时候它也会出现饱和的现象（在这种情况下通常称为dying ReLU）。Leaky ReLU[3]和PReLU[4]的提出正是为了解决这一问题。

（5）单调性（monotonic）：即导数符号不变。这个性质大部分激活函数都有，除了诸如sin、cos等。个人理解，单调性使得在激活函数处的梯度方向不会经常改变，从而让训练更容易收敛。

（6）输出范围有限：有限的输出范围使得网络对于一些比较大的输入也会比较稳定，这也是为什么早期的激活函数都以此类函数为主，如Sigmoid、TanH。但这导致了前面提到的梯度消失问题，而且强行让每一层的输出限制到固定范围会限制其表达能力。因此现在这类函数仅用于某些需要特定输出范围的场合，比如概率输出（此时loss函数中的log操作能够抵消其梯度消失的影响[1]）、LSTM里的gate函数。

（7）接近恒等变换（identity）：即约等于x。这样的好处是使得输出的幅值不会随着深度的增加而发生显著的增加，从而使网络更为稳定，同时梯度也能够更容易地回传。这个与非线性是有点矛盾的，因此激活函数基本只是部分满足这个条件，比如TanH只在原点附近有线性区（在原点为0且在原点的导数为1），而ReLU只在x>0时为线性。这个性质也让初始化参数范围的推导更为简单[5][4]。额外提一句，这种恒等变换的性质也被其他一些网络结构设计所借鉴，比如CNN中的ResNet[6]和RNN中的LSTM。

（8）参数少：大部分激活函数都是没有参数的。像PReLU带单个参数会略微增加网络的大小。还有一个例外是Maxout[7]，尽管本身没有参数，但在同样输出通道数下k路Maxout需要的输入通道数是其它函数的k倍，这意味着神经元数目也需要变为k倍；但如果不考虑维持输出通道数的情况下，该激活函数又能将参数个数减少为原来的k倍。

（9）归一化（normalization）：这个是最近才出来的概念，对应的激活函数是SELU[8]，主要思想是使样本分布自动归一化到零均值、单位方差的分布，从而稳定训练。在这之前，这种归一化的思想也被用于网络结构的设计，比如Batch Normalization[9]。

常用激活函数

1. Sigmoid

在这里插入图片描述
Sigmoid函数是一个在生物学中常见的S型函数，它能够把输入的连续实值变换为0和1之间的输出，如果输入是特别小的负数，则输出为0，如果输入是特别大的正数，则输出为1。即将输入量映射到0到1之间。
Sigmoid可以作为非线性激活函数赋予网络非线性区分能力，也可以用来做二分类。其计算公式为：
$\frac{1}{1+e^{-z}}$
导数：
$\frac{\partial f(z)}{\partial z} = f(z)\times (1-f(z))$

优点

曲线过渡平滑，处处可导；

缺点

幂函数运算较慢，激活函数计算量大；
求取反向梯度时，Sigmoid的梯度在饱和区域非常平缓，很容易造称梯度消失的问题，减缓收敛速度。

2. Tanh

在这里插入图片描述
Tanh是一个奇函数，它能够把输入的连续实值变换为-1和1之间的输出，如果输入是特别小的负数，则输出为-1，如果输入是特别大的正数，则输出为1；解决了Sigmoid函数的不是0均值的问题。
Tanh可以作为非线性激活函数赋予网络非线性区分能力。其计算公式为：
$\frac{e^z-e^{-z}}{e^z+e^{-z}}$
导数：
$\frac{\partial f(z)}{\partial z}=1-tan^2h(z)$

优点：

曲线过渡平滑，处处可导；
具有良好的对称性，网络是0均值的。

缺点：

与Sigmoid类似，幂函数运算较慢，激活函数计算量大；
与Sigmoid类似，求取反向梯度时，Tanh的梯度在饱和区域非常平缓，很容易造称梯度消失的问题，减缓收敛速度。

3. ReLU

在这里插入图片描述
线性整流函数（Rectified Linear Unit, ReLU），是一种深度神经网络中常用的激活函数，整个函数可以分为两部分，在小于0的部分，激活函数的输出为0；在大于0的部分，激活函数的输出为输入。计算公式为：
$f(x)=\begin{cases} x & x≥0 \\ 0 & x<0 \end{cases}$

导数：
$\frac {\partial f(x)}{\partial x}=\begin{cases} 1 & x≥0 \\ 0 & x<0 \end{cases}$

优点：

收敛速度快，不存在饱和区间，在大于0的部分梯度固定为1，有效解决了Sigmoid中存在的梯度消失的问题；
计算速度快，ReLU只需要一个阈值就可以得到激活值，而不用去算一大堆复杂的指数运算，具有类生物性质。

缺点：

它在训练时可能会“死掉”。如果一个非常大的梯度经过一个ReLU神经元，更新过参数之后，这个神经元的的值都小于0，此时ReLU再也不会对任何数据有激活现象了。如果这种情况发生，那么从此所有流过这个神经元的梯度将都变成 0。合理设置学习率，会降低这种情况的发生概率。

先进的激活函数

1. LeakyReLU

在这里插入图片描述
LeakyReLU是ReLU函数的改进版，普通的ReLU是将所有的负值都设为零，Leaky ReLU则是给所有负值赋予一个非零斜率，减缓存在负数时的梯度为零传播问题。其计算公式为：
$f(x)=\begin{cases} x & x≥0 \\ ax & x<0 \end{cases}$

导数：
$\frac {\partial f(x)}{\partial x}=\begin{cases} 1 & x≥0 \\ a & x<0 \end{cases}$

优点：

LeakyReLU具有ReLU的优点；
解决了ReLU函数存在的问题，防止死亡神经元的出现。

缺点：

α参数人工选择，具体的的值仍然需要讨论。

2. Swish

在这里插入图片描述

Swish是Sigmoid和ReLU的改进版，类似于ReLU和Sigmoid的结合，β是个常数或可训练的参数。Swish 具备无上界有下界、平滑、非单调的特性。Swish 在深层模型上的效果优于 ReLU。计算公式：
$f (x) = x \cdot s i g m o i d (β x)$

导数：
$\frac{\partial f(x)}{\partial x}=sigmoid(βx)+x·sigmoid'(βx)·β$

优点：

Swish具有一定ReLU函数的优点；
Swish具有一定Sigmoid函数的优点；
Swish函数可以看做是介于线性函数与ReLU函数之间的平滑函数。

缺点：

运算复杂，速度较慢。

5. Mish

在这里插入图片描述

Mish与Swish激活函数类似，Mish具备无上界有下界、平滑、非单调的特性。Mish在深层模型上的效果优于 ReLU。无上边界可以避免由于激活值过大而导致的函数饱和。
$f(x)=x * tanh(ln(1+e^x))$
导数：
$\frac{\partial f(x)}{\partial x}=tanh(ln(1+e^x))+x·tan'h(ln(1+e^x)·\frac{e^x}{1+e^x})$

优点：

Mish具有一定ReLU函数的优点，收敛快速；
Mish具有一定Sigmoid函数的优点，函数平滑；
Mish函数可以看做是介于线性函数与ReLU函数之间的平滑函数。

缺点：

运算复杂，速度较慢。

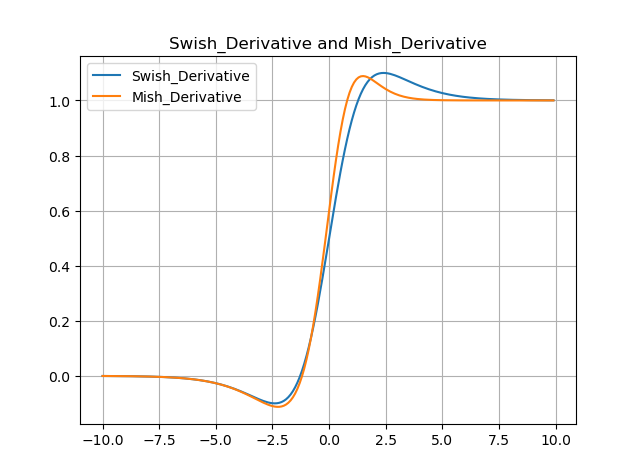
Swish和Mish函数从变化和变化率上都相接近

Numpy代码实现：

import matplotlib.pyplot as plt
import numpy as np

# Sigmoid
def sigmoid(x):
    return 1 / (1 + np.exp(-x))

def sigmoid_derivative(x):
    return sigmoid(x)*(1-sigmoid(x))

# tanh()
def tanh(x):
    # return np.tanh()
    return (np.exp(x)-np.exp(-x)) / (np.exp(x)+np.exp(-x))

def tanh_derivative(x):
    return 1-tanh(x)**2

# ReLU
def relu(x):
    return np.where(x<0, 0, x)

def relu_derivative(x):
    return np.where(x<0, 0, 1)

# LeakyReLu
def leakyrelu(x, a):
    return np.where(x < 0, a*x, x)

def leakyrelu_derivative(x, a):
    return np.where(x < 0, a, 1)

# Swish
def swish(x, b):
    return x*(1/(1+np.exp(-b*x)))

def swish_derivative(x, b):
    return sigmoid(b*x) + b*x*sigmoid_derivative(b*x)

# Mish
def mish(x):
    tmp = 1 + np.exp(x)
    return x * (tmp * tmp - 1) / (tmp * tmp + 1)

def mish_derivative(x):
    tmp = np.log(1+np.exp(x))
    return tanh(tmp) + x * tanh_derivative(tmp)*(np.exp(x)/(1+np.exp(x)))

if __name__=='__main__':
    x = np.arange(-10, 10, 0.1)

    plt.plot(x, sigmoid(x), label='Sigmoid')
    plt.plot(x, sigmoid_derivative(x), linestyle='--', label='Derivative')
    plt.title('Sigmoid')
    plt.legend()
    plt.grid()
    plt.show()

    plt.plot(x, tanh(x), label='Tanh')
    plt.plot(x, tanh_derivative(x), linestyle='--', label='Derivative')
    plt.title('Tanh')
    plt.legend()
    plt.grid()
    plt.show()

    plt.plot(x, relu(x), label='ReLU')
    plt.plot(x, relu_derivative(x), linestyle='--', label='Derivative')
    plt.title('ReLU')
    plt.legend()
    plt.grid()
    plt.show()

    plt.plot(x, leakyrelu(x, 0.1), label="LeakyReLU")
    plt.plot(x, leakyrelu_derivative(x, 0.1), linestyle='--', label="Derivative")
    plt.title('LeakyReLU')
    plt.legend()
    plt.grid()
    plt.show()

    plt.plot(x, swish(x, 1), label='Swish')
    plt.plot(x, mish(x), label='Mish')
    plt.title('Swish and Mish')
    plt.legend()
    plt.grid()
    plt.show()

    plt.plot(x, swish_derivative(x, 1), label='Swish_Derivative')
    plt.plot(x, mish_derivative(x), label='Mish_Derivative')
    plt.title('Swish_Derivative and Mish_Derivative')
    plt.legend()
    plt.grid()
    plt.show()

内容参考：https://blog.csdn.net/weixin_44791964/article/details/117338865?spm=1001.2014.3001.5501

Fighting_1997

关注

1
点赞
踩
7

收藏

觉得还不错? 一键收藏
打赏
0
评论
各类激活函数Activation Functions介绍及实现与优缺点分析

什么是激活函数？激活函数（Activation functions）对于神经网络模型学习与理解复杂和非线性的函数来说具有十分重要的作用。它们将非线性特性引入到我们的网络中。如果网络中不使用激活函数，网络每一层的输出都是上层输入的线性组合，无论神经网络有多少层，输出都是输入的线性组合。如果使用的话，激活函数给神经元引入了非线性因素，使得神经网络可以任意逼近任何非线性函数，此时神经网络就可以应用到各类非线性场景当中了。常见的激活函数如sigmoid、tanh、relu等，它们的输入输出映射均为非线性，这
复制链接

扫一扫