吴恩达《深度学习工程师》Part1.Week2 神经网络基础

2.1 二分分类
二分分类问题是根据输入$X$来判断其是否属于某种类型，用1和0来表示。

图1 判断图片中是否有猫的二分类问题
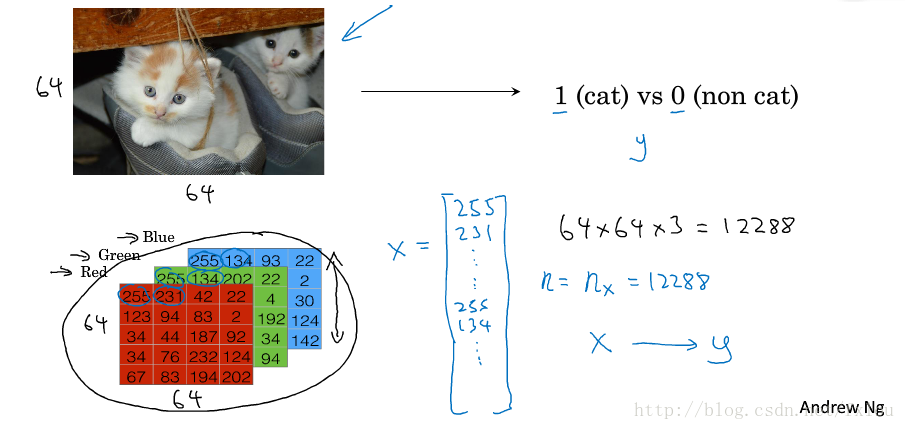
图1为一个典型的二分类问题。输入为一张RGB图片的三个通道亮度值，将这三个通道的亮度值依次排列出来构成了输入$X$，目标是判断图片中是否有猫，用输出$y=1$或$0$来表示。当输入图片数量为m个，纬度为$n_x$时，$X\in R^{n_x ×m}$, $y\in {\{0,1\}}$。

2.2 logistic回归
继续上节的判断图片是否有猫的问题，二分类问题直接预测输出为$1$或$0$，本节讲的logistic回归问题，则是根据输入$x\in R^{n_x}$，计算图片有猫的概率$\hat y=P(y=1|x)$。
最简单的办法是采用线性模型，将$x$乘上权重$w\in R^{n_x}$，再加上偏置$b$, 得到：

$$\hat y=w^T x+b$$
但是这样得到的$\hat y$极有可能小于$0$或大于$1$，而$\hat y$的取值范围只能是$0$到$1$之间。
logistic回归方法是将上面的$\hat y$代入到sigmoid函数中，$sigmoid(z)=\frac{1}{1+e^{-z}}$，其形状如图2所示。

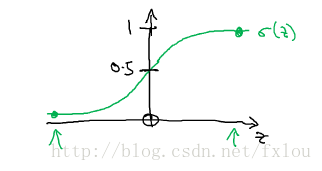
图2 sigmoid函数
sigmoid函数的函数值位于 $0$到$1$之间。最终，我们得到了logistic模型的形式如下：
$$\hat y=\frac{1}{1+e^{-(w^T x+b)}}$$
logistic模型的建模过程就是求解权重 $w$和$b$的过程。

2.3 logistic回归损失函数
判断logistic模型的好坏可以通过比较预测值$\hat y$和实际值$y$之间的差别来实现，这里我们定义一个损失函数（loss function）或者叫误差函数（error function）$L(\hat y,y)$，训练模型的过程就是寻找$w$和$b$，使得损失函数最小的过程。

损失函数其中一个选择是使用平方误差，$L(\hat y,y)=\frac{1}{2}(\hat y-y)^2$，但是这个损失函数在进行随机梯度下降时是非凸的，进行模型训练时只能得到局部最优解，很难得到全局最优解。

logistic回归分析使用的损失函数如下：

$$L(\hat y,y)=-(y log{\hat y}+(1-y)log(1-\hat y))$$
如果 $y=1$，则 $L(\hat y,y)=-log{\hat y}$，当 $w$和$b$的取值使得损失函数 $L(\hat y,y)$值最小时， $\hat y$值最大，即最接近于目标值1，预测效果最佳，此时的 $w$和$b$即为我们想要的模型参数。

如果$y=0$，则$L(\hat y,y)=-log(1-\hat y)$，当$w$和$b$的取值使得损失函数$L(\hat y,y)$值最小时，$\hat y$值最小，即最接近于目标值0，预测效果最佳，此时的$w$和$b$即为我们想要的模型参数。

损失函数是在单个样本上计算的，代价函数（cost function）则是在m个样本的训练集上定义的，如下式所示：

$$J(w,b)=\frac{1}{m}\sum_1^mL(\hat y^{(i)},y^{(i)})=-\frac{1}{m}\sum_1^my^{(i)}log{\hat y^{(i)}}+(1-y^{(i)})log(1-\hat y^{(i)})$$
根据一个训练集来计算 $w$和$b$时，要使得代价函数尽可能小。

2.4 梯度下降法
上节讲到，对logistic模型的训练过程就是寻找最佳的$w$和$b$使得代价函数$J(w,b)$最小的过程。代价函数$J(w,b)$是一个凸函数，其形状如图3所示。

图3 凸函数图示
其中 $w$可以是多维向量，这里为了方便绘图，采用了一维向量表示。
梯度下降法是一种重要的求解最优$w$和 $b$的方法，原理如下：

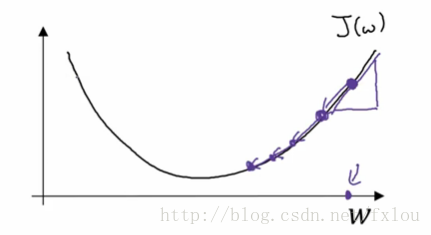
图4 梯度下降法
对于任意给定$w$初始值，根据 $w:=w-\alpha\cdot dw$进行更新，其中 $dw=\frac{\partial J(w,b)}{\partial w}$，从图4可以看出，随着 $w$的不断更新，代价函数$J$不断减小，直到到达最小值。

参数$b$的求解步骤跟$w$的一样。

2.5 导数
略
2.6更多导数的例子
略

2.7 计算图
神经网络的计算是通过前向传播（forward propagation）实现的，计算出输出，紧接着是反向传播（back propagation）过程，用来计算梯度，并更新参数$w$和$b$。
下面引入计算图的概念，例如计算$J=3(a+bc)$，可以用下图表示：

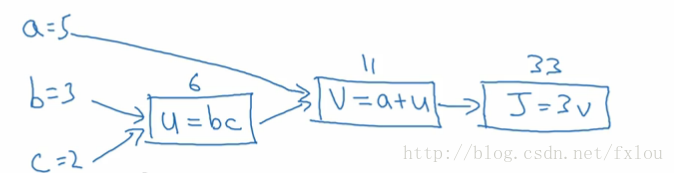
图5 一个简单的计算图

$J$的计算分解为几个不同的流程，这是一个类似于前向传播的过程。

2.8 计算图的导数计算
为了计算上节中的导数，可以按照下图进行：

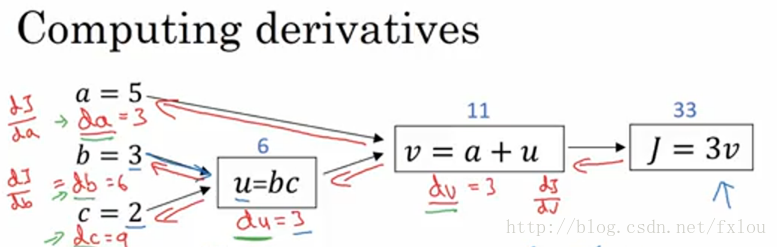
图6 计算图的导数计算流程

为了求出$\frac{dJ}{du}$，可以先计算出 $\frac{dJ}{dv}$，再计算出 $\frac{dv}{du}$，那么
$$\frac{dJ}{du}=\frac{dJ}{dv}\cdot\frac{dv}{du}$$
上式就是链式求导法则。

2.9 logistic回归中的梯度下降法
以单样本的logistic回归分析为例，说明如何进行梯度下降法。

图7 logistic回归分析主要步骤

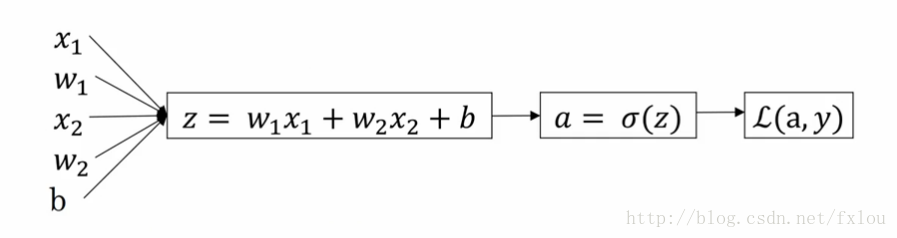
图8 单样本logistic回归分析流程图

logistic回归分析的过程是这样的，先进行向前传播，根据初始权重 $W$、偏置$b$和输入 $X$，计算出预测值$\hat y$，再进行反向传播，计算出权重 $W$、偏置$b$的导数，并对其进行更新，也就是2.4节讲到的梯度下降法步骤。

在计算权重$W$、偏置$b$的导数时，可以根据流程图的分解来分部计算，依次求出：
$\frac{\partial L}{\partial a}=-\frac{y}{a}+\frac{1-y}{1-a}$
$\frac{\partial a}{\partial z}=a(1-a)$
$\frac{\partial z}{\partial w1}=x_1$
$\frac{\partial z}{\partial w2}=x_2$
$\frac{\partial z}{\partial b}=1$
利用链式求导法则，得到：
$\frac{\partial L}{\partial w1}=（a-y）x_1$
$\frac{\partial L}{\partial w2}=（a-y）x_2$
$\frac{\partial L}{\partial b}=（a-y）$
采用梯度下降法对$W$和$b$进行更新：
$w:=w-\alpha\cdot\frac{\partial L}{\partial w}$
$b:=b-\alpha\cdot\frac{\partial L}{\partial b}$

2.10 m个样本的梯度下降
上节的梯度下降是对单个样本进行的计算，优化的目标函数是损失函数$L$。当给定一个包含$m$个数据的训练集时，优化的是代价函数$J$，2.3节讲到，

$$J(w,b)=\frac{1}{m}\sum_1^mL(\hat y^{(i)},y^{(i)})$$
因此
$\frac{\partial J}{\partial w_1}=\frac{1}{m}\sum_1^m\frac{\partial L^{(i)}}{\partial w_1}$
$\frac{\partial J}{\partial w_2}=\frac{1}{m}\sum_1^m\frac{\partial L^{(i)}}{\partial w_2}$
$...$
$\frac{\partial J}{\partial b}=\frac{1}{m}\sum_1^m\frac{\partial L^{(i)}}{\partial b}$

实现以上计算过程的伪代码如下：

J=0,dw1=0,dw2=0,...,b=0
for i =1 to m:
    z[i]=w.T*x[i]+b
    a[i]=sigmoid(z[i])
    J+=-(y[i]*log(a[i])+(1-y[i])*log(1-a[i]))
    dz[i]=a[i]-y[i]
    dw1+=dz[i]*x1[i]
    dw2+=dz[i]*x2[i]
    ...
    b+=dz[i]

J/=m
dw1/=m
dw2/=m
...
b/=m

在得到以上的$dw_1,dw_2,..,b$值以后，应用一次梯度下降法，对$W$和$b$进行更新。
不过上面的代码中存在多个for循环，而for循环在深度学习的训练中会严重影响代码运行效率，下节将讲到如何使用向量化（Vectorization）的方法来替代for循环，从而提高计算效率。

2.11 向量化
在进行logistic回归分析时，输入$X$一般是一维向量，$X\in R^{n_x}$，权重$W$也是一维向量，$W\in R^{n_x}$，那么在计算$z=W^T\cdot X+b$时，如果使用for循环，则代码如下：

w=[w_1,w_2,...,w_nx],x=[x_1,x_2,x_nx]
z=0
for i in range(n_x):
    z+=w[i]*x[i]
z+=b

如果在python中用向量化来实现的话，可以直接用以下代码：

w=[w_1,w_2,...,w_nx],x=[x_1,x_2,x_nx]
import numpy as np
z=np.dot(w,b)+b

经过测试，向量化比for循环计算效率高300倍。
在CPU和GPU中都有并行化的指令，有时被成为SIMD（Single instruction multiple data）指令，意味着如果使用类似np.dot这样的指令，能够充分利用并行化进行计算，显著提高计算效率。

2.12 向量化的更多例子
对2.10节中的logistic回归分析求梯度值的代码进行向量化改进，新的代码如下：

import numpy as np
'''
J=0,dw1=0,dw2=0,...,b=0 
the previous line changes to the following line'''
J=0,dw=np.zeros((n_x,1)),...,b=0
for i =1 to m:
    z[i]=w.T*x[i]+b
    a[i]=sigmoid(z[i])
    J+=-(y[i]*log(a[i])+(1-y[i])*log(1-a[i]))
''' dz[i]=a[i]-y[i]
    dw1+=dz[i]*x1[i]
    dw2+=dz[i]*x2[i]
    ...         
    the previous lines changes to the following line'''
    dw=dz[i]*x[i]
    b+=dz[i]

J/=m
'''dw1/=m
dw2/=m
...
the previous line changes to the following line
'''
dw/=m
b/=m

2.13 向量化logistic回归
在logistic回归分析计算激活值$z$时，输入$W,X$均为向量，可以直接用以下代码实现：

Z=np.dot(W.T,X)+b
A=sigmoid(Z)

其中W.T是对W的转置操作，上述代码还使用了Python中的广播（broadcasting）功能。sigmoid函数是用户自定义的可以将向量Z作为输入，并输出向量A的函数。

2.13 向量化logistic回归的梯度输出
上节已经可对$A$实现了向量化，又有标签$Y$是向量化的，则$dZ$可以直接计算：

db=np.sum(dZ)/m
dw=np.dot(X,dZ.T)/m

总结起来，完整的向量化logistic回归分析代码为：

Z=np.dot(W.T,X)+b
A=sigmoid(Z)
dZ=A-Y
dw=np.dot(X,dZ.T)/m
db=np.sum(dZ)/m
w-=alpha*dw
b-=alpha*db

2.15 至2.17
略
2.18 Logistic损失函数的解释
Logistic回归分析预测的函数$\hat y$表达式为：$\hat y=sigmoid(w^Tx+b)$
$\hat y$是已知$x$时，$y=1$的概率值：$\hat y = P(y=1|x)$
当$y=1$时，预测得到的概率就等于$\hat y$
当$y=0$时，预测得到的概率则等于$1-\hat y$
想要把这两个式子整合在一起，可以使用下面的函数：

$$P(y|x)={\hat y} ^y(1-{\hat y}) ^{1-y}$$
对于单个数据，Logistic模型获得最优的预测效果，意味着概率 $P(y|x)$取最大值，由于 $log$函数为单调递增函数，最大化 $P(y|x)$等价于最大化 $log(P(y|x))$。由于进行梯度下降法时，目标函数要求最小值，因此在前面加上负号，这样损失函数就变为：
$$L({\hat y}^{(i)},y^{(i)})=-log(P(y|x))=-(\hat y logy+(1-\hat y)log(1-y))$$

当在m个数据的训练集上进行训练时，需要这m个数据的联合概率最大化，即联合概率分布最大化（这里假设m个样本服从独立同分布IID）

$$max\prod_1^mP(y^{(i)}|x^{(i)})$$
这就是极大似然估计（Maximum Likelihood Estimate，MLE），由于 $log$函数为单调递增函数，对上式进行 $log$运算：
$$max\sum_1^m-L({\hat y}^{(i)},y^{(i)})$$
由于梯度下降法要对优化目标函数求最小值，上式加入负号，为了便于后面的计算，进行缩放，除以m，得到：
$$min\frac {1}{m}\sum_1^mL({\hat y}^{(i)},y^{(i)})$$