Complex Conjugate Pole Analysis for Bandwidth
二阶系统理论公式

如果有三阶多项式,会产生一对共轭复极点和一个实数极点
![]()
![]() 阻尼因子和自然频率
阻尼因子和自然频率![]() 是实极点
是实极点
上式中如果γ很大,可以写作![]()
电路与等效电路

传输函数

(1)电阻反馈,电感为0

(2)电感反馈

带宽公式



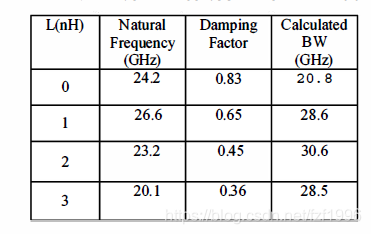
通过改变电感可以改变带宽

Complex Conjugate Pole Analysis for Bandwidth
二阶系统理论公式

如果有三阶多项式,会产生一对共轭复极点和一个实数极点
![]()
![]() 阻尼因子和自然频率
阻尼因子和自然频率![]() 是实极点
是实极点
上式中如果γ很大,可以写作![]()
电路与等效电路

传输函数

(1)电阻反馈,电感为0

(2)电感反馈

带宽公式



通过改变电感可以改变带宽


 1728
1728

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?


