目录
note:
通解+特解
拉氏变换
状态空间 /矩阵方法
二阶常系数线性微分方程
定义
y''+py'+qy = f(x) // p, q 为常数
- f(x)= 0 二阶常系数齐次线性微分方程
- f(x)≠ 0 二阶常系数非齐次线性微分方程
补充性质:
齐次方程解法

特征根三种情况:
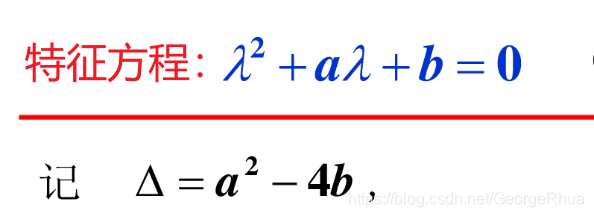
1. Δ > 0 两个相异实根

2. Δ = 0 两个相等实根

3. Δ < 0 一对共轭复根

拉氏变换基础知识
-
定义

-
典型函数的拉氏变换




-
性质
1. 线性性质

2. 微分性质

第二项开始,s的次数减少至0,f(0) 阶数增加至 n-1
3.积分
(待补充)
4.中值定理

-
反变换
常用部分分式法
例题:








 本文主要介绍了二阶常系数线性微分方程的基础概念及其解法,包括齐次与非齐次方程的求解方法,并讨论了特征根的三种情形。此外还介绍了拉氏变换的基本概念及其在线性微分方程求解中的应用。
本文主要介绍了二阶常系数线性微分方程的基础概念及其解法,包括齐次与非齐次方程的求解方法,并讨论了特征根的三种情形。此外还介绍了拉氏变换的基本概念及其在线性微分方程求解中的应用。


















 1827
1827

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








