前言
翻开《概率论与数理统计》(第四版)的第四章,你会看到“随机变量的数值特征”几个字。学了概率论这么久,该好好把这章总结一下。这章的知识在理论和实际应用真的很重要,特别是在数据分析处理的时候。
1 数学期望
简称期望,又叫均值。记作E(X),完全由随机变量X的概率分布所确定。
离散型随机变量X:P{ X = Xi } = Pi , i = 1 ,2 ,3 ,······
级数能收敛,其数学期望:
连续型随机变量X,其概率密度为f(x),
积分能收敛,其数学期望:
几个重要的性质:
- E(C) = C ,C为常数;
- E(CX) = CE(X) ,C为常数;
- E(X + Y) = E(X) + E(Y),X、Y为随机变量
- E(XY) = E(X)E(Y) ,X、Y是相互独立的随机变量
2 方差
方差,是为了度量随机变量与其均值(期望)的偏离程度。
定义:设X是一个随机变量,若E{ [ X - E(X) ]^2 }存在,则称E{ [ X - E(X) ]^2 }为X的方差,记为D(X)或Var(X),即:
D(X) = Var(X) = E{ [ X - E(X) ]^2 } (2.1)
D(X)越小,X的值越集中在E(X)的附近;反之,则越分散。
对于离散型随机变量X:
对于连续型随机变量X:
其中,f(x)是X的概率密度。
计算公式:D(X) = Var(X) = E(X^2) - E(X)^2 (2.4)
有个标准化变量的概念:设随机变量X具有数学期望E(X) = μ,方差D(X) = σ^2(不为0)。记X* = (X - μ) / σ,则
X* = (X - μ) / σ的数学期望为0,方差为1。X*称为X的标准化量。
几个重要的性质:
- D(C) = 0 , C是常数
- D(CX) = C^2D(X) , D(X + C) = D(X) , X是随机变量,C是常数
- D(X + Y) = D(X) + D(Y) + 2E{ ( X - E(X) )( Y - E(Y) ) } , X、Y是两个随机变量
- D(X + Y) = D(X) + D(Y) , X、Y是两个相互独立的随机变量
切比雪夫(Chebyshev)不等式:
设随机变量X具有数学期望E(X) = μ,方差D(X) = σ^2,则对于任意正数ε,不等式:
成立。
3 协方差及相关系数
协方差用于描述X和Y之间相互关系的数值特征。
定义:量E{ [X - E(X)][( Y - E(Y)] }称为随机变量X与Y的协方差。记做Cov(X ,Y),即
Cov(X ,Y) = E{ [X - E(X)][( Y - E(Y)] }
相关系数:
根据方差的知识,对于任意两个随机变量X和Y,下列等式成立:
D(X + Y) = D(X) + D(Y) + 2Cov(X , Y)
计算协方差的公式:Cov(X , Y) = E(XY) - E(X)E(Y)
几个重要的性质:
- Cov(aX , bY) = abCov(X , Y) , a,b是常数
- Cov(X1 + X2 , Y) = Cov(X1 , Y) + Cov(X2 ,Y)
相关系数的两个重要性质:
相关系数是用来表征X、Y之间线性关系紧密程度的量。系数较大,X、Y线性相关程度较好;较小,X、Y线性相关程度较差。为零时,X、Y不相关。
4 矩、协方差矩阵
定义:设(X ,Y)是二维随机变量,
X的k阶原点矩,简称k阶矩:
X的k阶中心矩:
X和Y的k+l阶混合中心矩:
随机变量(X1 , X2)的协方差矩阵:
(X1 , X2)有四个二阶中心矩,分别记为:
c11 = E{ [X1 - E(X1)]^2 } , c12 = E{ [X1 - E(X1)][X2 - E(X2)] } ,c12 = E{ [X2 - E(X2)][X1 - E(X1)] } , c22 = E{ [X2 - E(X2)]^2 }
矩阵形式:
n维随机变量(X1,X2,... ,Xn)的协方差矩阵:
几个重要的性质:
- n维正态随机变量(X1,X2,... ,Xn)的每一个分量Xi , i = 1,2,......n 都是正态随机变量;反之,若X1,X2,... ,Xn 都是正态随机变量,且相互独立,则(X1,X2,... ,Xn)是n维正态随机变量。
- n维随机变量(X1,X2,... ,Xn)服从n维正态分布的充要条件是X1,X2,... ,Xn的任意的线性组合 l1X1 + l2X2 + ... +lnXn 服从一维正态分布(其中l1,l2,...ln不全为零)。
- 若(X1,X2,... ,Xn)服从n维正态分布,设Y1,Y2,... ,Yk是Xj(j = 1,2, .... , n)的线性函数,则(Y1,Y2,... ,Yk)也服从多维正态分布。
-
设(X1,X2,... ,Xn)服从n维正态分布,则“X1,X2,... ,Xn相互独立”与“X1,X2,... ,Xn两两不相关”是等价的。











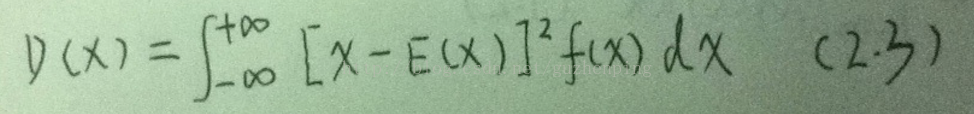






















 1189
1189

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








