3.4多维随机变量的特征数

类似于一维随机变量的特征数，多维随机变量也有特征数，除了各个分量的期望、方差、标准差以外，还有两个随机变量间的关联程度，即协方差与相关系数，这是一种反映两个随机变量相依关系的特征数，需要特别注意。

1 多维随机变量函数的数学期望

为了简单起见，我们用二维随机变量叙述此定理，而对n维随机变量的结论是类似的。

定理3.4.1 若二维随机变量$(X,Y)$的分布用联合分布列$P(X=x_i,Y=y_i)$或用联合密度函数$p(x,y)$表示，则$Z=g(X,Y)$的数学期望为：

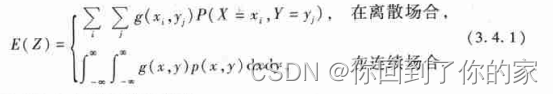
还要指出，在连续场合（离散场合也类似）有：

2 数学期望与方差的运算性质

性质 3.4.1 设$(X,Y)$是二维随机变量，则有：

$$E(X,Y)=E(X)+E(Y)(3.4.2)$$

性质 3.4.2 若随机变量$X$与$Y$相互独立，则有：

$$E(XY)=E(X)E(Y)(3.4.4)$$

待补充 188

证明：设定$(X,Y)$为连续随机变量（对离散随机变量可类似证明）其联

性质 3.4.3 若随机变量$X$与$Y$相互独立，则有：

$$Var(X\pm Y)=Var(X)+Var(Y)$$

这个性质表明：独立变量代数和的方差等于各方差之和。

这个性质可推广到n维随机变量场合，即若$X_1,X_2,\cdots ,X_n$相互独立，则有：

待补充 188

3 协方差

二维联合分布中除含有各分量的边际分布外，还含有两个分量间相互关联的信息。描述这种相互关联程度的一个特征数就是协方差，它的定义如下：

定义3.4.1 设$(X,Y)$是一个二维随机变量，若$E[(X-E(X))(Y-E(Y))]$存在，则称此数学期望为$X$与$Y$的协方差，或称$X$与$Y$的相关（中心）矩，并记为：

$$Cov(X,Y)=E[(X-E(X))(Y-E(Y))]$$

特别有$Cov(X,X)=Var(X)$。

协方差可正可负，也可以为零，其具体表现如下：

• 当$Cov(X,Y)>0$时，称$X$与$Y$正相关，这时两个偏差$(X-E(X))$与$(Y-E(Y))$有同时增加或者同时减少的倾向。由于$E(X)$与$E(Y)$都是常数，故等价于$X$与$Y$有同时增加或同时减少的倾向，这就是正相关的含义。
• 当$Cov(X,Y)<0$时，称$X$与$Y$负相关，这时有$X$增加而$Y$减少的倾向，或有$Y$增加而$X$减少的倾向，这就是负相关的含义。
• 当$Cov(X,Y)<0$时，称$X$与$Y$不相关。这时可能由两类情况导致：一类是$X$与$Y$的取值毫无关联（见性质3.4.5），另一类是$X$与$Y$之间存有某种非线性关系（见例3.4.6）。

下面的性质在协方差的计算中是很有用的：

性质3.4.4 $Cov(X,Y)=E(XY)-E(X)E(Y)$

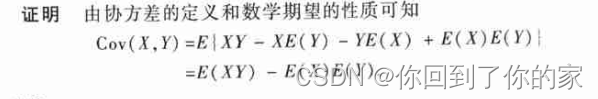
下面的性质表明：“不相关”是比“独立”更弱的一个概念。

协方差概念的引入可以完善随机变量和的方差计算，如下面的性质：

性质3.4.6 对任意的二维随机变量$(X,Y)$，有：

$$Var(X\pm Y)=Var(X)+Var(Y)+\pm 2Cov(X,Y)(3.4.8)$$

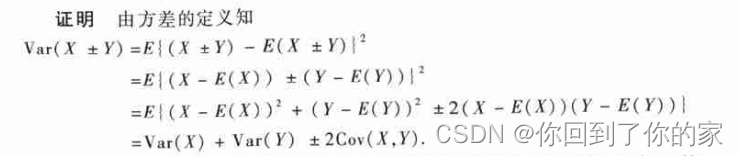
这个性质表明：在X与Y相关的场合，和的方差不等于方差的和。X与Y的正相加会增加和的方差，负相关会减少和的方差，而在X与Y不相关的场合，和的方差等于方差的和。

性质3.4.6还可以推广到更多个随机变量场合，即对任意n个随机变量$X_1,X_2,\cdots ,X_n$，有：

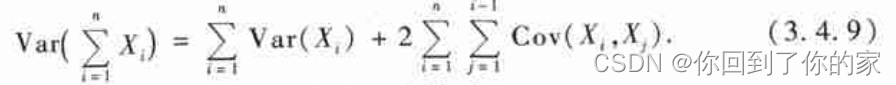
关于协方差的计算，还有下面四条有用的性质。

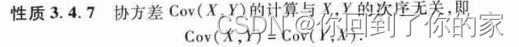
待补充 192