旋转变压器软件解码可能指的是将当前的旋转变压器的数据进行解码,以便在计算机中进行处理和分析。具体来说,需要进行以下步骤:
-
获取旋转变压器的原始数据。这可以通过传感器或其他数据采集设备来实现。
-
将原始数据输入计算机,利用特定的软件对数据进行解码。这需要使用与旋转变压器相对应的解码算法。
-
对解码后的数据进行分析和处理。这可以包括对变压器的运行状态进行监测,检测变压器是否存在故障或异常。
-
根据需要,生成报告或输出其他形式的数据。这可以帮助维护人员及时发现问题并进行处理。
需要注意的是,不同类型的旋转变压器可能需要不同的解码算法和软件,因此需要根据具体情况进行选择。
本文实现MATLAB纯软件实现解码,包括信号旋变模拟发出到,旋变信号解码.
旋变格式信号

旋变器是一种旋转变压器,通常配置是初级绕组位于转子
上,两个次级绕组则位于定子上。不过,可变磁阻旋变器
的转子上不存在绕组,如图24所示。初级绕组和次级绕组
均位于定子上,但转子的特殊设计使得次级耦合随着角位
置变化而发生正弦变化。无论何种配置,旋变输出电压(S3
− S1, S2 − S4)的计算公式均相同,如公式1所示。


两个定子绕组机械错位90°(参见图24)。初级绕组采用交流
基准源激励。随后在定子次级绕组上的耦合的幅度是转子
(轴)相对于定子的位置的函数。因此,旋变产生由轴角的
正弦和余弦调制的两个输出电压(S3 − S1, S2 − S4)。旋变格
式信号是指从旋变输出获得的信号,如公式1所示。图25
为输出格式的示意图。

下图为MATLAB仿真信号源

激励信号10Khz.

分解器到数字转换器块为将旋转轴的角位置或速度转换为电信号的转换器建模。分解器到数字转换器通常用于恶劣、崎岖的环境,例如全电动汽车。
转换后的信号与轴角度的正弦或余弦成比例。
旋转变压器传感器有一个转子绕组,励磁机正弦波交流耦合到两个定子绕组。定子绕组,一个正弦线圈和一个余弦线圈,机械定位成90度异相。当转子旋转时,转子位置角相对于定子绕组发生变化。然后必须获得、解调和后处理得到的幅度调制信号,以提取角度和速度信息([1]和[2])。
方程式
该块使用锁相环(PLL)来提取旋转轴的角度和速度。PI控制器使用的误差电压如下所示:
![]()
Vp是激励电压。
Vx是旋转变压器次级绕组的x电压。
Vy是旋转变压器次级绕组的y电压。
N是旋转变压器的极对数。
θ是角度。
获得的速度为:
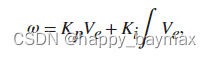
使用以下公式根据速度计算角度:

可调节参数如下
Sample time (-1 for inherited) — Block sample time
采样时间(-1表示继承)-块采样时间
Phase-looked loop proportional gain — PLL proportional gain
锁相环比例增益
Phase-looked loop integral gain — PLL integral gain
锁相环积分增益-PLL积分增益
Number of pole pairs — Pole pairs in the attached machine
极对数-所附机器中的极对数


Np为4,信号源100hz,角度信号频率100/4=25(HZ);角速度为100/4*2*pi=157 rad/s;
锁相参数待优化,角速度有震荡.
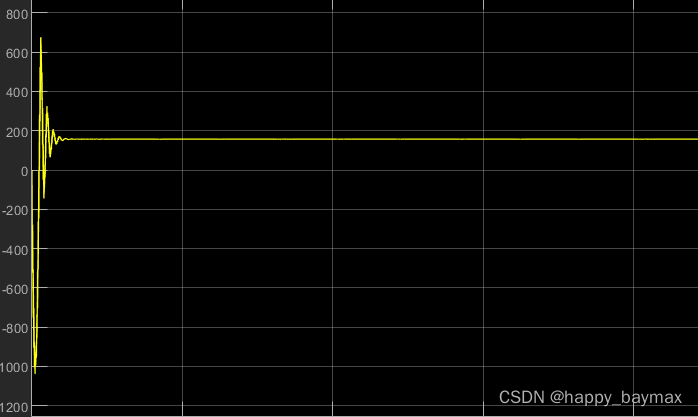







 文章介绍了旋转变压器的工作原理,特别是MATLAB中如何进行软件解码,包括使用锁相环和PI控制器来提取角度和速度信息。针对10kHz激励信号,讨论了角速度震荡问题及参数优化需求。
文章介绍了旋转变压器的工作原理,特别是MATLAB中如何进行软件解码,包括使用锁相环和PI控制器来提取角度和速度信息。针对10kHz激励信号,讨论了角速度震荡问题及参数优化需求。

















 1929
1929

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?










