【SLAM】状态估计系统和卡尔曼滤波

1.状态估计

> 状态估计（state estimation）根据可获取的量测数据估算动态系统内部状态的方法。对系统的输入和输出进行测量而得到的数据只能反映系统的外部特性，而系统的动态规律需要用内部（通常无法直接测量）状态变量来描述。因此状态估计对于了解和控制一个系统具有重要意义。状态估计（state estimation）根据可获取的量测数据估算动态系统内部状态的方法。对系统的输入和输出进行测量而得到的数据只能反映系统的外部特性，而系统的动态规律需要用内部（通常无法直接测量）状态变量来描述。因此状态估计对于了解和控制一个系统具有重要意义。

按照之前讨论所讲，我们对于2帧之间进行估计，这是一种时间暂时性估计，就是短期的，但是SLAM系统是一个长期运行的系统，我们希望长期估计相机的位姿运动等等。这就是需要一定的状态估计的知识。

上图是我们假设的系统状态。

x为状态，z为观测。很明显观测方程的数量要远远多于状态方程。用方程表达一个系统，加上高斯噪声。

对于非线性优化问题，我们可以使用最大似然估计法，将最大似然估计问题转化为最小二乘问题的求解。

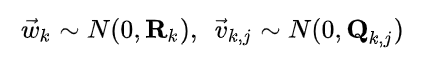
我们假设当前观测为u和z，需要估计x和y。

这个问题就转换为了最大似然值了。

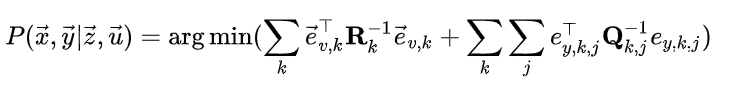
2.卡尔曼滤波

> 卡尔曼滤波（Kalman filtering）是一种利用线性系统状态方程，通过系统输入输出观测数据，对系统状态进行最优估计的算法。由于观测数据中包括系统中的噪声和干扰的影响，所以最优估计也可看作是滤波过程。
数据滤波是去除噪声还原真实数据的一种数据处理技术，Kalman滤波在测量方差已知的情况下能够从一系列存在测量噪声的数据中，估计动态系统的状态。由于它便于计算机编程实现，并能够对现场采集的数据进行实时的更新和处理，Kalman滤波是目前应用最为广泛的滤波方法，在通信，导航，制导与控制等多领域得到了较好的应用。

当我们假设当前状态只和上一个状态有关时，就隐含了马尔可夫性，这是一种估计状态的方法。

推导过程如下：
e(k|k-1)=X(k)-X(k|k-1)=A( x(k)-x(k-1|k-1) ) + W(k)
P(k|k-1)=E{ ( X(k) - X(k|k-1) ) ( X(k) - X(k|k-1) )’}
=E{ ( AX(k-1)+BU(k)+W(k)-AX(k-1|k-1)-BU(k) ) ( AX(k-1) + BU(k) + W(k) - AX(k-1|k-1) - BU(k) )’}
=E{ ( A( X(k-1) - X(k-1|k-1) ) + W(k) ) ( A( X(k-1) - X(k-1|k-1) )+W(k) )’}
=E{ A( X(k-1) - X(k-1|k-1) ) ( X(k-1)-X(k-1|k-1) )’A’+ W(k)W(k)’}
=A E{ ( X(k-1) - X(k-1|k-1) ) ( X(k-1) - X(k-1|k-1) )’} A’+ E{ W(k)W(k)’}
=A P(k-1|k-1) A’+ Q

这里不做过多赘述。

3.实践

接下来我们通过程序来理解一下这个卡尔曼滤波的原理：

function output = kalmanFilter(data, Q, R, N)
 
if ~exist('Q', 'var')
    Q = 0.01;
end
if ~exist('R', 'var')
    R = 1;
end
if ~exist('N', 'var')
    N = 0;
end
 
X = 0;
P = 1;
A = 1;
H = 1;
 
output = zeros(size(data));
 
for ii = N + 1 : length(data)
   X_k = A * X;
   P_k = A * P * A' + Q;
   Kg = P_k * H' / (H * P_k * H' + R);
   z_k = data(ii - round(rand() * N));
   X = X_k + Kg * (z_k - H * X_k);
   P = (1 - Kg*H) * P_k;
   output(ii) = X;
end
 
end

由于卡尔曼滤波存在各种各样的问题，我们在如今的slam系统中更多的使用非线性优化的方法，不再使用卡尔曼滤波。

再来一个例子，这个实例希望大家自己分析结果。

%-------------------------------------------------------------------------
% DESC: Simulation of measured voltage measurements with 0.1 volt RMS white 
%       noise (actual voltage should be -0.37727 volts).
% The Kalman filter is used to estimate the optimal voltage value.
%-------------------------------------------------------------------------

clear all; clc;

N=50; 
x(1)=0;  %初始估计状态
p(1)=1;  %初始估计协方差
Q=10^-6;  %过程噪声的协方差
R=10^-2;  %观测噪声的协方差
t=1:N; 

%---------------------NOISY MEASUREMENT-----------------------------------
voltage = [-0.46687,-0.36375,-0.39117,-0.49361,-0.2589,-0.37881,-0.32365,...
    -0.44891,-0.44283,-0.34583,-0.36659,-0.19245,-0.40478,-0.15601,-0.22642,...
    -0.57178,-0.54532,-0.43462,-0.39585,-0.37638,-0.29358,-0.4495,-0.44942,...
    -0.39739,-0.37932,-0.34938,-0.27144,-0.3151,-0.55233,-0.30754,-0.29612,...
    -0.31364,-0.24626,-0.34456,-0.44457,-0.3922,-0.62217,-0.32994,-0.36558,...
    -0.43638,-0.44274,-0.48534,-0.38204,-0.33934,-0.41031,-0.42726,-0.38087,...
    -0.39475,-0.473,-0.24802;];
%-------------------------------------------------------------------------

for i=2:N 
    y(i)=x(i-1); %预测的状态
    p1(i)=p(i-1)+Q; %预测的协方差
    kg(i)=p1(i)/(p1(i)+R); %卡尔曼增益
    x(i)=y(i)+kg(i)*(voltage(i)-y(i)); %更新的状态
    p(i)=(1-kg(i))*p1(i); %更新的协方差 
end 

plot(t,x,'r');
hold on 
plot([0 50],[-0.37727 -0.37727],'k');
plot(voltage,'-b');
axis([0 50 -0.7 0]);
xlabel('time');
ylabel('voltage');

4.小结：

通常情况，在计算资源严重受限的时候，我们会使用卡尔曼滤波，但是，现有的非线性优化的方法要优于卡尔曼滤波的方法，因为卡尔曼滤波有着马尔可夫性的假设，我们在slam系统中更加希望使用全局的状态来估计下一个状态，所以非线性优化无疑是一个更好的办法。