g2o中 EdgeSE3Expmap类型Jacobian的计算

位姿优化的时候，两个顶点的类型是SE3，涉及到的误差雅克比是pose error对pose的求导，里面有些知识值得注意，故记录下来。

前期准备

重新翻看Ethan Eade的《Lie Groups for 2D and 3D Transformations》，发现他的文档早已有相关推导。比如针对两个SO3乘积对其中一个求导：

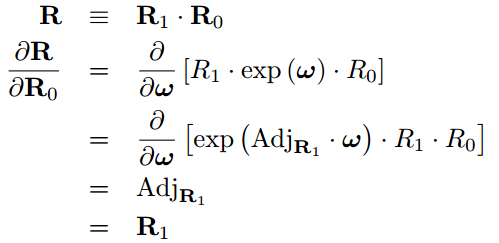
比如同理两个SE3乘积, 对其中一个求导：

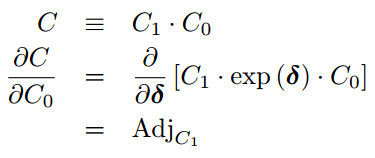
上面这两个推导都利用了adjoint的性质。这部分Ethan Eade的文档中有，也可参看strasdat phd thesis 2.4.7部分的定义：

$$\exp([{adj_T\cdot{\xi}}]_{\times})=T\exp(\hat{\xi})T^{-1}$$
由上面的公式可以简单得到如下性质， 这个性质要牢记，预积分里反复用到了:
$$\color{blue}{T\exp(\hat{\xi})=T\exp(\hat{\xi})T^{-1}T=\exp([{adj_T\cdot{\xi}}]_{\times})T }\\ \color{blue}{\exp(\hat{\xi})T^{-1}=T^{-1}\exp([{adj_T\cdot{\xi}}]_{\times})}$$
很容易看出，当 $T$和$exp()$相乘时，利用这个性质可以调换它们的乘法位置，左乘变右乘，这在求导的时候十分有用。
稍加改变有：
$$\exp(\hat{\xi})T=T\exp([{adj_{T^{-1}}\cdot{\xi}}]_{\times})$$
同时可以计算出 $adj_T$的计算公式(Ethan Eade文档)：

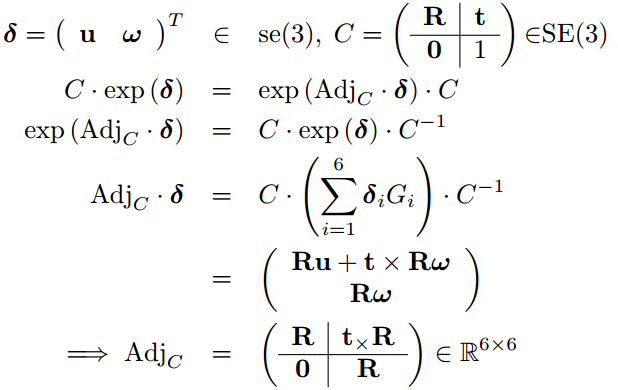
EdgeSE3Expmap中雅克比推导

有了Ethan文档的雅克比推导，EdgeSE3Expmap中雅克比的计算依葫芦画瓢就行了。首先通过代码看图优化里位姿边的误差定义，types_six_dof_expmap.h 文件第118行:

    void computeError()  {
      const VertexSE3Expmap* v1 = static_cast<const VertexSE3Expmap*>(_vertices[0]);
      const VertexSE3Expmap* v2 = static_cast<const VertexSE3Expmap*>(_vertices[1]);

      SE3Quat C(_measurement);
      SE3Quat error_= v2->estimate().inverse()*C*v1->estimate();
      _error = error_.log();
    }

写成公式形式如下:

$$T_{err} =T_{jw}^{-1}{\hat{T}_{ji}}T_{iw}$$
其中 $\hat{T}_{ji}$表示位姿变换的测量。

上面误差公式是多个位姿相乘的形式，所以借鉴前面的推导过程，下面开始对误差的雅克比进行推导，先看下g2o代码的实现，types_six_dof_expmap.cpp 文件第274行，可以看到求得的导数也是某个位姿的adj()形式，所以验证了推导思路没错:

void EdgeSE3Expmap::linearizeOplus() {
  VertexSE3Expmap * vi = static_cast<VertexSE3Expmap *>(_vertices[0]);
  SE3Quat Ti(vi->estimate());

  VertexSE3Expmap * vj = static_cast<VertexSE3Expmap *>(_vertices[1]);
  SE3Quat Tj(vj->estimate());

//注意这里把测量标记为Tij应该是标记错误了，应该是Tji，不然整个误差公式说不通了
//这个可以看orbslam EdgeSim3里添加测量时就是用的Sji
  const SE3Quat & Tij = _measurement;　　　// shoulb be Tji
  SE3Quat invTij = Tij.inverse();

  SE3Quat invTj_Tij = Tj.inverse()*Tij;
  SE3Quat infTi_invTij = Ti.inverse()*invTij;

  _jacobianOplusXi = invTj_Tij.adj();
  _jacobianOplusXj = -infTi_invTij.adj();
}

误差雅克比中误差对变量$X_j$(位姿j)的推导，也就是微小增量作用在位姿j上：

$$T_{err} =T_{jw}^{-1}{\hat{T}_{ji}}T_{iw}\\ \xi_{err}=log(T_{err}) \\ T_{err}(\delta\xi_{j'j}) =(\exp(\widehat{\delta\xi_{j'j}}) T_{jw})^{-1}{\hat{T}_{ji}}T_{iw} \\ \qquad \qquad=T_{jw}^{-1} \color{Red}{\exp(-\hat{\delta\xi}_{j'j}){\hat{T}_{ji}}T_{iw}} \\ \qquad \qquad \qquad \qquad \qquad = T_{jw}^{-1}\color{Red}{{\hat{T}_{ji}}T_{iw}\exp([-adj_{({\hat{T}_{ji}}T_{iw})^{-1}}\cdot\delta\xi_{j'j}]_{\times})} \\ \qquad \qquad \qquad \qquad \qquad\qquad\qquad\quad= \exp(\hat{\xi}_{err})\exp(-[adj_{({\hat{T}_{ji}}T_{iw})^{-1}}\cdot\delta\xi_{j'j}]_{\times}) \qquad\qquad(*)$$ (*)式要是连个幂指数是矩阵的相乘，这时候要用barfoot 状态估计一书的公式7.80展开
$$T_{err}(\delta\xi_{j'j}) =\exp([{\xi}_{err}-J_r({\xi}_{err})^{-1}adj_{({\hat{T}_{ji}}T_{iw})^{-1}}\cdot\delta\xi_{j'j}]_{\times})\\ log(T_{err}(\delta\xi_{j'j}))={\xi}_{err}-J_r({\xi}_{err})^{-1}adj_{({\hat{T}_{ji}}T_{iw})^{-1}}\cdot\delta\xi_{j'j}$$
注意误差 ${\xi}_{err}\approx 0$，所以 $J_r({\xi}_{err})^{-1}\approx I$，因此误差对位姿j的雅克比为:
$$\frac{\Delta log(T_{err}(\delta\xi_{j'j}))}{\Delta\delta\xi_{j'j}} = -adj_{({\hat{T_{ji}}}T_{iw})^{-1}}$$
和代码 $jacobianOplusXj = -infT_i\_invT_{ji}.adj()$对应, 注意g2o那个EdgeSE3雅克比代码里写的是 $Tij$应该为 $Tji$.
对 $T_{iw}$的更新雅克比有两个思路，一个是完全仿照上面的过程，如下
$$T_{err} =T_{jw}^{-1}{\hat{T}_{ji}}T_{iw}\\ \xi_{err}=log(T_{err}) \\ T_{err}(\delta\xi_{i'i}) =T_{jw}^{-1}{\hat{T}_{ji}}\exp(\widehat{\delta\xi_{i'i}})T_{iw} \\ \qquad \qquad \qquad \qquad \qquad = T_{jw}^{-1}{\hat{T}_{ji}}\color{Red}{T_{iw}\exp([adj_{(T_{iw})^{-1}}\cdot\delta\xi_{i'i}]_{\times})}$$
得到
$$J_{xi}= adj((T_{iw})^{-1})$$
这个雅克比猛一看和代码中的不一样，注意上面推导过程中是把 $exp(\widehat{\delta\xi_{i'i}})$这一项往右边移动的，同理，我们可以把他往左边移动。
$$T_{err}(\delta\xi_{i'i}) =T_{jw}^{-1}{\hat{T}_{ji}}\exp(\widehat{\delta\xi_{i'i}})T_{iw} \\ \qquad \qquad \qquad \qquad \qquad =\color{Red}{\exp([adj_{(T_{jw}^{-1}{\hat{T}_{ji}})}\cdot\delta\xi_{i'i}]_{\times})T_{jw}^{-1}{\hat{T}_{ji}}} T_{iw}$$
这时候使用BCH公式的另一个，并近似 $J_l \approx I$, 就能得到
$$J_{xi}=adj(T_{jw}^{-1}{\hat{T}_{ji}})$$
这个和代码里是符合的，猛一看前一个推导不一样，但其实他俩近似。因为，在忽略误差的情况下有 $T_{jw}^{-1}{\hat{T}_{ji}}=T_{wi}$，所以可以认为上面两个 $J_{xi}$的推导方式都是正确的。但是搞不清为啥g2o中要这么弄.