m基于Berlekamp-Massey钱搜索算法的BCH译码误码率matlab仿真

目录

1.算法仿真效果

2.算法涉及理论知识概要

3.MATLAB核心程序

4.完整算法代码文件

---

1.算法仿真效果

matlab2022a仿真结果如下：

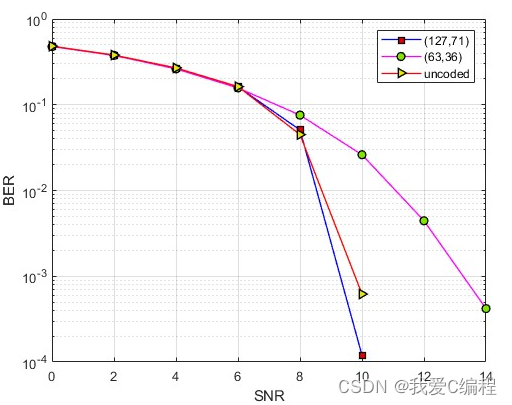
2.算法涉及理论知识概要

      BCH编译码是一种纠错能力强，构造简单的信道编译码。BCH编译码的生成多项式可以由如下的式子表示：

  

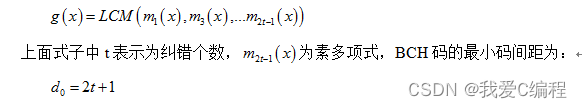
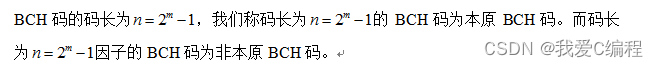
①BCH码是一种纠错码、线性分组码、循环码。

②需要传输信息位数：k

③纠错能力：t

④总码长（信息位+监督位）：n

⑤n的长度满足n=2^m – 1时生成的为本原BCH码；n的长度为2^m – 1的因子时为非本原BCH码

（如n=15，n=31，n=63时为本原BCH码；n=21（可被63整除）等时为非本原BCH码）

⑥此外还有加长BCH码和缩短BCH码。

⑦具体的BCH码通常用BCH（n,k）码来表示。

加长BCH码和缩短BCH码：
因为本原BCH码和非本原BCH码要求了n的长度，但很多情况下我们想要的码长并不满足n=2^m – 1或其因子。这时候就需要加长BCH码和缩短BCH码。

（1）缩短BCH码

BCH(50,32)码是扩展域GF(2^6)上BCH(63,45)码的缩短码。BCH(50,32)码和BCH(63,45)码的区别与联系：

①两者纠错能力相同，生成多项式相同。

②缩短码的实现只需要在编译码时在高位上补0，从k = 32凑到k = 45即可。

（2）加长BCH码

在本原BCH码或非本原BCH码的生成多项式中乘因式(x+1)，可以得到加长BCH码(n+1,k)，加了一个校验位。

  编码之后的码字包含信息字节和校验字节，其表达式如下所示：

         BCH译码过程主要通过计算伴随式sj得到错误位置多项式，然后通过chein算法计算错误位置多项式的根，从而确定错误位置数。并最终由错误位置数得到错误值以及错误图样E(x)，最后通过R(x)- E(x)= C(x)进行纠错。

---

 

3.MATLAB核心程序

%begin decoding
for j=1:nwords
    rec_data=rec_data2((j-1)*n+1:(j-1)*n+n);
    syndrome=gf(zeros(1, 2*t), m);
    for i=1:n,
        syndrome=syndrome.*alpha_tb+rec_data(n-i+1);
    end;
    %imba
    lambda = gf([1, zeros(1, t)], m);
    lambda0= lambda;
    b=gf([0, 1, zeros(1, t)], m);
    b2 = gf([0, 0, 1, zeros(1, t)], m);
    k1=0;
    gamma = one;
    delta = zero;
    syndrome_array = gf(zeros(1, t+1), m);

    if(simplified == 1) 
        for r=1:t,
            r1 = 2*t-2*r+2;
            r2 = min(r1+t, 2*t);
            num = r2-r1+1;
            syndrome_array(1: num) = syndrome(r1:r2);
            delta = syndrome_array*lambda';
        
            lambda0 = lambda;
            lambda = gamma*lambda-delta*b2(2:t+2);
        
            if((delta~= zero) && (k1>=0))
                b2(3)=zero;
                b2(4:3+t) = lambda0(1:t);
                gamma = delta;
                k1 = -k1;
            else
            b2(3:3+t) = b2(1:t+1);
            gamma = gamma;
            k1=k1+2;
            end
            joke=1;
        end
    else
        for r=1:2*t,
            r1 = 2*t-r+1;
            r2 = min(r1+t, 2*t);
            num = r2-r1+1;
            syndrome_array(1:num) = syndrome(r1:r2);
            delta = syndrome_array*lambda';

            lambda0 = lambda;
            lambda = gamma*lambda-delta*b(1:t+1);

            if((delta ~= zero) && (k1>=0))
                b(2:2+t)=lambda0;
                gamma = delta;
                k1=-k1-1;
            else
                b(2:2+t) = b(1:t+1);
                gamma = gamma;
                k1=k1+1;
            end   
            joke=1;
        end
    end

    %inverstable
    inverse_tb = gf(zeros(1, t+1), m);
    for i=1:t+1,
        inverse_tb(i) = alpha^(-i+1);
    end;

    %chien's search
    lambda_v = zero;
    accu_tb=gf(ones(1, t+1), m);
    for i=1:n,
        lambda_v=lambda*accu_tb';
        accu_tb = accu_tb.*inverse_tb;
        if(lambda_v==zero)
            error(1,n-i+1)=1;
        else
            error(1,n-i+1)=0;
        end
    end
    found = find(error(1,:)~=0);
    for i=1:length(found)
        location=found(i);
        if location <= k;
            rec_data(n-location+1)=rec_data(n-location+1)+one;
        end
    end
    decoded_data((j-1)*k+1:(j-1)*k+k)=rec_data(n-k+1:n);
end

%decoded_data;
error=0.;
for i=1:length(message)
    if message(i)~=decoded_data(i)
        error=error+1;
    end
end
ber = error/length(message);
14_047_m

4.完整算法代码文件

V