回归模型-岭回归和lasso回归★★★

云上西

于 2024-07-21 20:47:32 发布

阅读量1.1k

点赞数 14

分类专栏：清风建模数学建模文章标签：回归数据挖掘人工智能数学建模算法 python 机器学习

本文链接：https://blog.csdn.net/huahua121_/article/details/140592671

版权

数学建模同时被 2 个专栏收录

41 篇文章

订阅专栏

清风建模

29 篇文章

订阅专栏

该博客为个人学习清风建模的学习笔记，部分课程可以在B站：【强烈推荐】清风：数学建模算法、编程和写作培训的视频课程以及Matlab等软件教学_哔哩哔哩_bilibili

名称	重要性	难度
岭回归和lasso回归	★★★	★★★★

博主其他回归模型地址：回归模型-多元线性回归分析★★★★★-CSDN博客

在第七讲时，我们介绍了多元线性回归模型，估计回归系数使用的是OLS，并在最后探讨了异方差和多重共线性对于模型的影响。事实上，回归中关于自变量的选择大有门道，变量过多时可能会导致多重共线性问题造成回归系数的不显著，甚至造成OLS 估计的失效。

本节介绍到的岭回归和lasso 回归在 OLS 回归模型的损失函数上加上了不同的惩罚项，该惩罚项由回归系数的函数构成，一方面，加入的惩罚项能够识别出模型中不重要的变量，对模型起到简化作用，可以看作逐步回归法的升级版；另一方面，加入的惩罚项能够让模型变得可估计，即使之前的数据不满足列满秩，在稍后的原理推导中我们将更加详细的说明这一点。

1古典回归模型

古典回归模型需要满足以下四点假定：

1.1线性假定

1.2严格外生性

保证估计出来的回归系数无偏且一致

1.3无完全多重共线性

保证系数能够估计出来

1.4球型扰动项

2岭回归

岭回归 (Ridge regression: Hoerl and Kennard, 1970) 的原理和 OLS 估计类似，但是对系数的大小设置了惩罚项。

如何选择 $\lambda$ 呢?

2.1岭迹分析

使用少，主观性太强

2.2VIF法

2.3最小化均方预测误差

3Lasso回归

4应用

在 Stata 中，我们可以安装 lassopack 命令来实现 Lasso 回归，Lassopack 包含三个与 Lasso 相关的子命令（输入 help lassopack 可以查看详情）： ‐ 子命令 lasso2 可进行 Lasso 估计； ‐ 子命令 cvlasso 可进行 K 折交叉验证（ k‐fold cross validation ）； ‐ 子命令 rlasso 可以估计惩罚项由数据决定或者高维情形（变量维度超过样本数）。

另外，大多数博客或讲义上都是使用Python 来做岭回归和 lasso 回归的，因此有 python 机器学习基础的同学可以自己查阅相关的调用代码。

另外， Stata 中对于岭回归的估计有点 bug ，因此我们下面只讲 Lasso 回归的估计，有兴趣的同学可以看这个文章：https://zhuanlan.zhihu.com/p/53905488

4.1安装lassopack命令

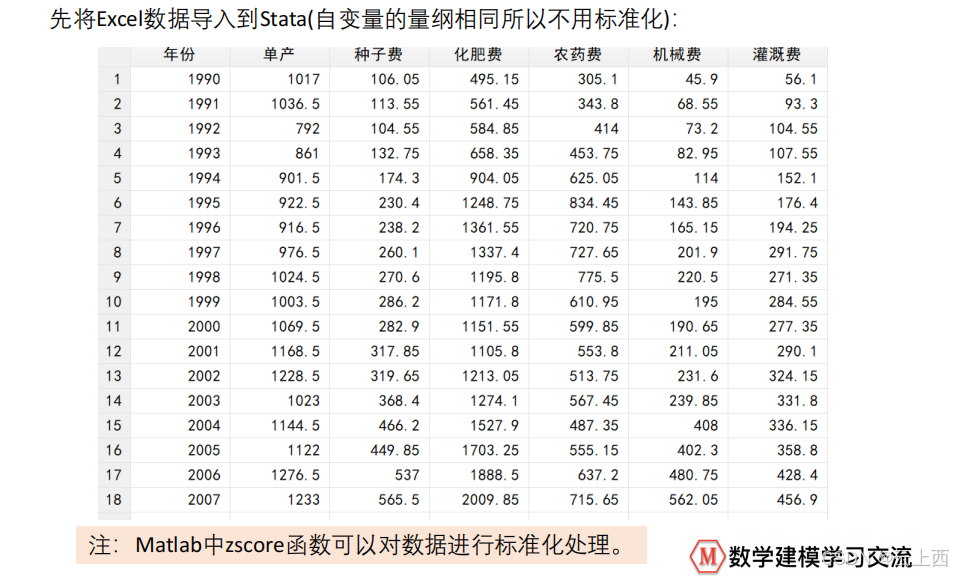
4.2分析棉花产量例题

4.3代码

// 清空工作区数据
clear
// 安装lassopack命令,见课件
// findit lassopack   
// 导入数据，注意修改Excel文件的地址
import excel "C:\Users\hc_lzp\Desktop\数学建模视频录制\A01更新\岭回归和lasso回归\数据和拓展资料\棉花产量论文作业的数据.xlsx", sheet("data") firstrow
// 注意：这里自变量的量纲相同所以不用标准化，如果需要标准化，那么可以借助Matlab的zscore函数，或者直接使用SPSS（分析-描述统计-描述：在描述列表的方框左下角，看到“将标准化得分另存为变量（Z）之后点击打勾，然后确定。）
// Stata中也有相应的标准化变量的命令，不过一次只能标准化一个变量，例如： egen Y = std(单产)   这个代码就表示将单产标准化，得到的变量记为Y
cvlasso 单产 种子费 化肥费 农药费 机械费 灌溉费, lopt seed(520)