Gradient Descent、Momentum、Nesterov的实现及直觉对比

最新推荐文章于 2025-02-27 14:11:27 发布

秦伟H

最新推荐文章于 2025-02-27 14:11:27 发布

阅读量1.6k

点赞数 3

分类专栏：深度学习机器学习 tensorflow 轻松上手TensorFlow 文章标签： Momentum Nesterov 梯度下降动量牛顿动量

本文链接：https://blog.csdn.net/huqinweI987/article/details/83247659

版权

机器学习同时被 3 个专栏收录

27 篇文章

订阅专栏

深度学习

23 篇文章

订阅专栏

tensorflow

19 篇文章

订阅专栏

GradientDescent、Momentum（动量）、Nesterov（牛顿动量）的直觉含义对比：

Gradient Descent

def gd(x_start, step, g):#gradient descent
    x = np.array(x_start, dtype='float64')
    # print(x)
    passing_dot = [x.copy()]#training record
    for i in range(50):
        grad = g(x)
        x -= grad * step

        passing_dot.append(x.copy())
        print('[ epoch {0} ]   grad={1},   x={2}'.format(i, grad, x))
        if abs(sum(grad)) < 1e-6:#early stop
            break
    return x, passing_dot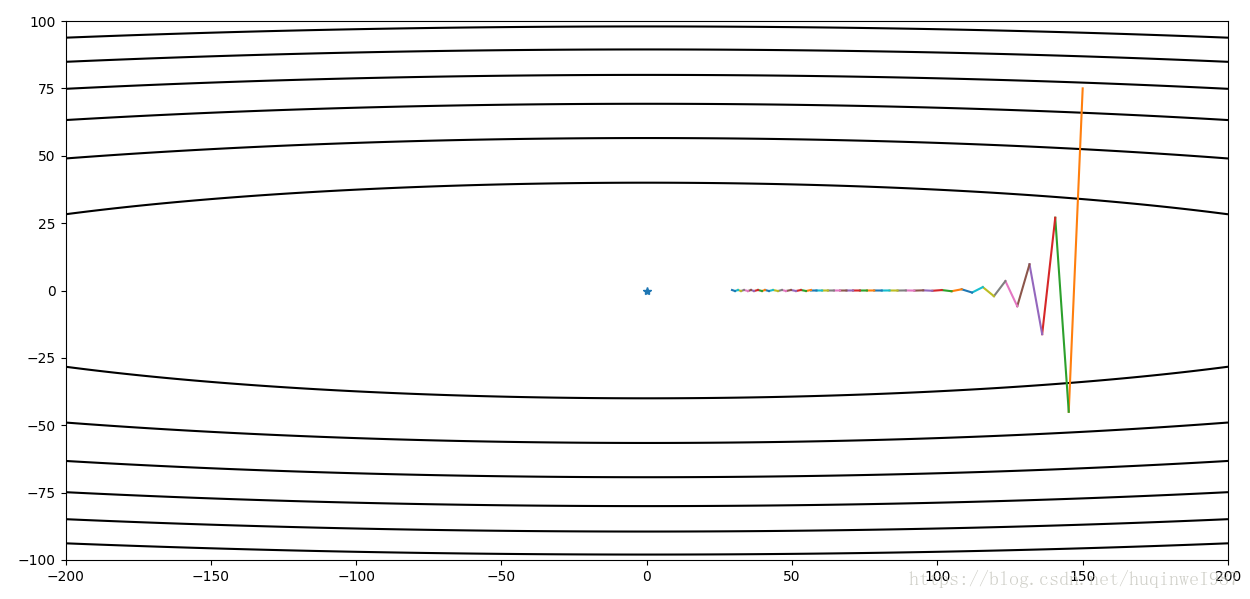

就是有一步走一步，走到哪算哪，比如本例走个之字（zigzag），初期纵向步子大，上下来回绕（如果学习率再大点就不收敛了），后期纵向收敛。但是横向步子小（因为横向纵向梯度不一样，纵向梯度大，横向梯度小），最后没有什么更新动力，最终在50步内没有到达中心点。

Momentum

def momentum(x_start, step, g, discount = 0.7):
    x = np.array(x_start, dtype='float64')
    passing_dot = [x.copy()]
    pre_grad = np.zeros_like(x)

    for i in range(50):
        grad = g(x)
        pre_grad = pre_grad * discount + grad
        x -= pre_grad * step
        passing_dot.append(x.copy())

        print('[ Epoch {0} ] grad = {1}, x = {2}'.format(i,grad,x))
        if abs(sum(grad)) < 1e-6:
            break
    return x, passing_dot

Momentum会保留之前步子的趋势（动量），相比Gradient Descent走过头以后直接返回，Momentum返回“中心”的初期也会向外拉你一把，让你不那么容易回到“正轨”，单纯看这一阶段确实是变慢了——劣势（伏笔），但是宏观上是利大于弊，累加起来以后会越来越稳，最后直接这个把你往外跳的趋势也给拉没了。所以，其实动量算法的抗噪声能力很强。（深度学习很多时候没有全场景全阶段的最优，只有综合的最优，trade off的结果，理论上的最优只有手工干预才能办到）

刚才的例子不明显，下边增加一下学习率：同样学习率下，Gradient Descent可能不收敛，而Momentum还能收敛，并且需要很少的步子就能办到。而在横轴方向，Momentum也因为动量累积效应，很容易达到了中心点。这是同样条件下Gradient Descent所没有办到的。

动量衰减的大小意味着之前的趋势是否难以撼动。如果动量衰减很小，也就是discount数值很大，也是不容易收敛的，但是随着步数积累，动量衰减的幂次也增多，还是有收敛的趋势的。

本例比较简单，条件不极端，极端情况下，同方向累积步数过多，如果动量衰减程度低，反而要比Gradient Descent波动还大，所以超参数discount的选择也很重要。

左图，小学习率同方向积累多步情况下，过大discount导致不易收敛（至少是在有限步数下，和前边同条件对比）；右图，同学习率下，普通Gradient Descent纵轴早已收敛（因为横纵比例问题，横向停留，前边提过）。但是如果横纵综合起来看，再提升总的训练步数，Gradient Descent还是远不如Momentum的结果好。

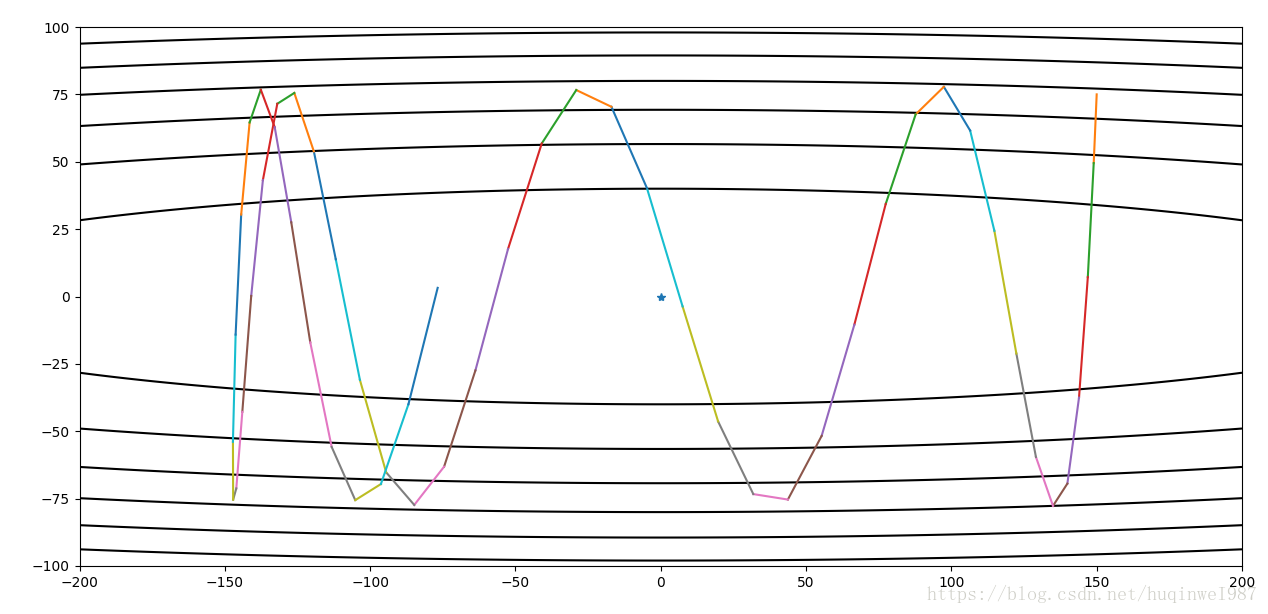
可变的discount也可考虑，初期需要的discount小，防止加速逃逸，后期需要的discount大，稳定步伐、加速收敛。

顺便在同学习率下，剧透一个Nesterov效果：

Nesterov

def nesterov(x_start, step, g, discount = 0.7):
    x = np.array(x_start, dtype='float64')
    passing_dot = [x.copy()]
    pre_grad = np.zeros_like(x)
    for i in range(50):
        x_future = x - step * discount * pre_grad
        grad = g(x_future)
        pre_grad = pre_grad * discount  + grad 
        x -= pre_grad * step

        passing_dot.append(x.copy())
        print('[ Epoch {0} ] grad = {1}, x = {2}'.format(i,grad,x))
        if abs(sum(grad)) < 1e-6:
            break
    return x, passing_dot

Nesterov是Momentum的变种，或者叫Nesterov动量，是受Nesterov算法启发改进的Momentum算法。它是先走到你下一步将要到的那个点，然后把那个“未来的点”的梯度计算出来（取代当前点的地位），直接更新动量和x。

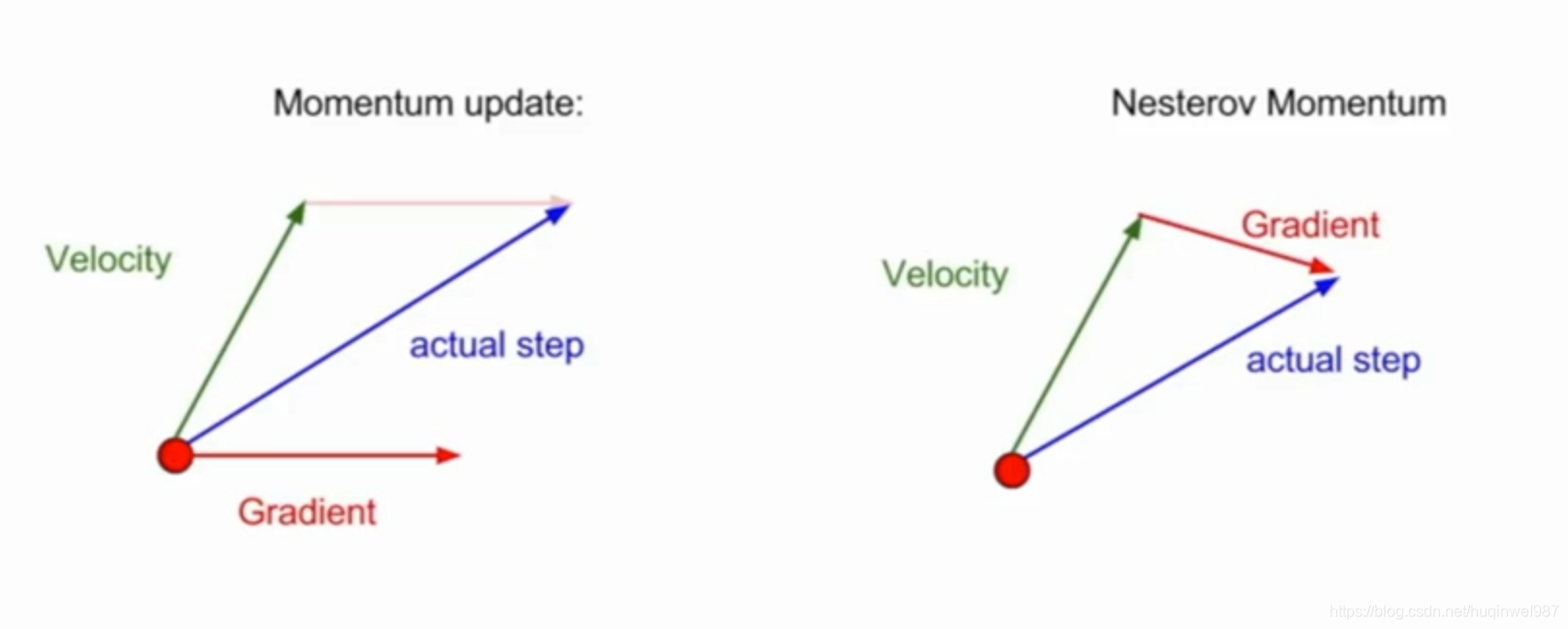
如上图，实际中不光是单方向的正负叠加，还包括多方向，所以最终Momentum向量符合平行四边形法则，而Nesterov，略有不同。

这个特性就非常有意思了，进行第一步之后，如果“第三步”的方向和当前运动方向不一致，如果是Momentum，第二步仍然朝着固有方向前进（加速逃逸），而Nestrov，就会在第二步就提前产生反向的纠正，把x拉回去；如果第三步和运动方向一致，也不会产生放大效应，不会有double位移，因为跳过了第二步，只是“旧三步”替代“旧二步”变成了“新二步”。那么再迭代一次，顶多也就是用新分支下的“新四步”来代替“新三步”成为“新新三步”（因为还是要产生新分支），然后是“新新新四步”，以此类推。

好处：学习率合适，如果下一步趋势不变，可以看做等价替换；如果下一步有加速、减速或者掉头的趋势，又能提前实现。

左图Nesterov、右图Momentum

右图向量2是按Momentum本该有的行进路线，3是2结束后的下一步行进路线。1结束后就有了向下的动量，2带着1的向下的趋势多走了一段，“拉不回来”可以算是Momentum的一个劣势。但是Nesterov就不同了，它是“预判加截停”，知道你要去哪个方向，直接绕你前边往回打一巴掌。也就是从向量2的终点去找向量3，近似的看作向量3平移（不是2+3）成了向量4，也就是左图的向量2。这个算法是对Momentum的进一步优化，算是一个修正。本例，直觉地说，前期走过站的操作更容易拉回来了。（前边和Gradient Descent对比时的伏笔，Nesterov解决了这个问题）

下边是Nesterov的第二种写法，这种写法更像《深度学习》算法8.3，而且看着更简洁。

不过两种写法最终效果一样，区别只是pre_grad（动量v）是先乘过step还是在更新x时再乘step。


def nesterov2(x_start, step, g, discount = 0.7):
    x = np.array(x_start, dtype='float64')
    passing_dot = [x.copy()]
    pre_grad = np.zeros_like(x)
    for i in range(50):
        x_future = x - discount * pre_grad
        grad = g(x_future)
        pre_grad = pre_grad * discount + grad * step
        x -= pre_grad

        passing_dot.append(x.copy())
        print('[ Epoch {0} ] grad = {1}, x = {2}'.format(i,grad,x))
        if abs(sum(grad)) < 1e-6:
            break
    return x, passing_dot
# res, x_arr = nesterov([150,75], 0.012, g)
res, x_arr = nesterov2([150,75], 0.0034, g)
contour(X,Y,Z,x_arr)

完整代码：https://github.com/huqinwei/tensorflow_demo/blob/master/simple_demo/Momentum_Nesterov_GD.py