机器学习中的数学——常用概率分布（五）：高斯分布（Gaussian分布）/正态分布（Normal分布）

分类目录：《机器学习中的数学》总目录
相关文章：
· 常用概率分布（一）：伯努利分布（Bernoulli分布）
· 常用概率分布（二）：范畴分布（Multinoulli分布）
· 常用概率分布（三）：二项分布（Binomial分布）
· 常用概率分布（四）：均匀分布（Uniform分布）
· 常用概率分布（五）：高斯分布（Gaussian分布）/正态分布（Normal分布）
· 常用概率分布（六）：指数分布（Exponential分布）
· 常用概率分布（七）： 拉普拉斯分布（Laplace分布）
· 常用概率分布（八）：狄拉克分布（Dirac分布）
· 常用概率分布（九）：经验分布（Empirical分布）
· 常用概率分布（十）：贝塔分布（Beta分布）
· 常用概率分布（十一）：狄利克雷分布（Dirichlet分布）
· 常用概率分布（十二）：逻辑斯谛分布（Logistic 分布）

---

实数上最常用的分布就是正态分布，也称为高斯分布：
$$N(x|\mu ,{\sigma }^2)=\sqrt{\frac{1}{2\pi {\sigma }^2}}{e}^{-\frac{(x-\mu {)}^2}{2{\sigma }^2}}$$

其中：

• $E[x]=\mu$
• $Var(x)=pi{\sigma }^2$

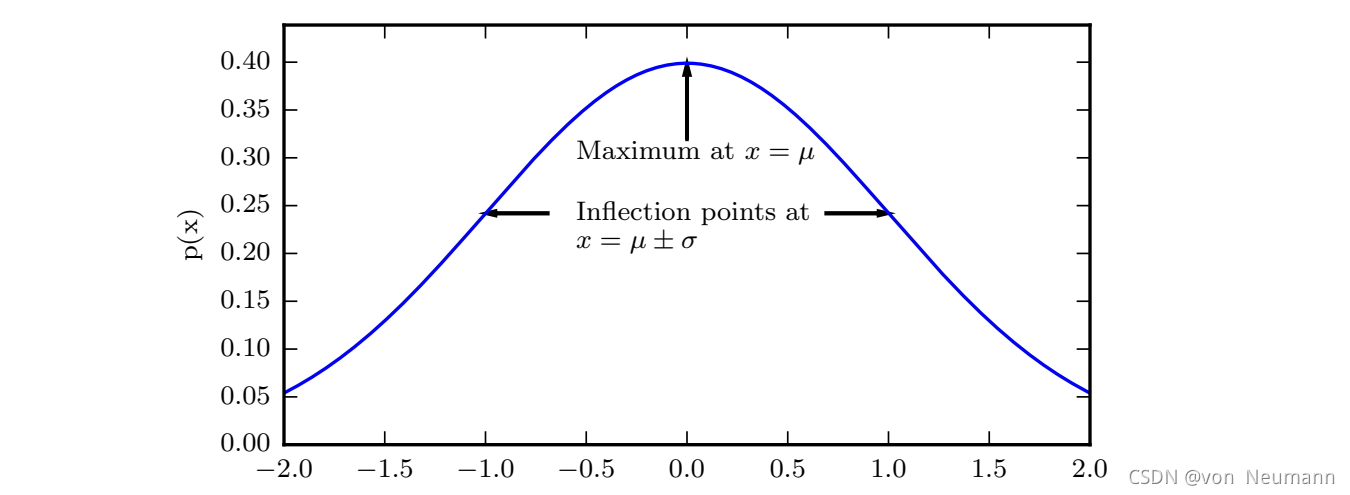
正态分布由两个参数控制，$\mu \in R$和$\sigma \in (0,\infty )$。参数$\mu$给出了中心峰值的坐标，这也是分布的均值：$E[x]=\mu$。分布的标准差用$\sigma$表示，方差用${\sigma }^2$表示。

当我们要对概率密度函数求值时，我们需要对${\sigma }^2$取倒数。当我们需要经常对不同参数下的概率密度函数求值时，一种更高效的参数化分布的方式是使用参数$\beta \in (0,\infty )$，来控制分布的精度：
$$N(x|\mu ,{\beta }^{-1})=\sqrt{\frac{\beta }{2\pi }}{e}^{-\frac{1}{2}\beta (x-\mu {)}^2}$$

采用正态分布在很多应用中都是一个明智的选择。当我们由于缺乏关于某个实数上分布的先验知识而不知道该选择怎样的形式时，正态分布是默认的比较好的选择，其中有两个原因：

1. 我们想要建模的很多分布的真实情况是比较接近正态分布的。中心极限定理说明很多独立随机变量的和近似服从正态分布。这意味着在实际中，很多复杂系统都可以被成功地建模成正态分布的噪声，即使系统可以被分解成一些更结构化的部分。
   在具有相同方差的所有可能的概率分布中，正态分布在实数上具有最大的不确定性。因此，我们可以认为正态分布是对模型加入的先验知识量最少的分布。

正态分布可以推广到$R^n$）。它的参数是一个正定对称矩阵$\Sigma$：
$$N(x|\mu ,\Sigma )=\sqrt{\frac{1}{(2\pi {)}^n\text{det}(\Sigma )}}{e}^{-\frac{1}{2}(x-\mu {)}^T{\Sigma }^{-1}(x-\mu )}$$

参数$\mu$仍然表示分布的均值，只不过现在是向量值。参数$\Sigma$给出了分布的协方差矩阵。和单变量的情况类似，当我们希望对很多不同参数下的概率密度函数多次求值时，协方差矩阵并不是一个很高效的参数化分布的方式，因为对概率密度函数求值时需要对$\Sigma$求逆。我们可以使用一个精度矩阵$\beta$进行替代：
$$N(x|\mu ,{\beta }^{-1})=\sqrt{\frac{\text{det}(\beta )}{(2\pi {)}^n}}{e}^{-\frac{1}{2}(x-\mu {)}^T\beta (x-\mu )}$$

我们常常把协方差矩阵固定成一个对角阵。一个更简单的版本是各向同性高斯分布，它的协方差矩阵是一个标量乘以单位阵。