一文读懂方向导数与梯度

一文读懂方向导数与梯度

转载请注明出处，或注明转载自“黄邦勇帅(原名：黄勇)

单位向量e的两种表示，e = ai + bj和e = i cos α + j cos β ，其中α、β为单位向量的方向角，为了更直观，本文使用e = i cos α + j cos β 这一表示

一、单位向量表示的直线的参数方程

1、使用单位向量表示的直线的参数方程
设e = ( cos α , cos β )为一单位向量，l是xOy面上通过点P ( x0 , y0 )且以e为方向向量的直线，由空间解析几何知，直线l的参数方程可表示为

注意： cos α 和cos β并不是相互独立的，由于单位向量e = ( cos α , cos β )，因此，他们有关系cos² α + cos² β = 1

二、方向导数的定义及其几何意义

1、偏导数反映的是函数沿坐标轴方向的变化率，而方向导数研究的是函数沿任一指定方向的变化率问题。

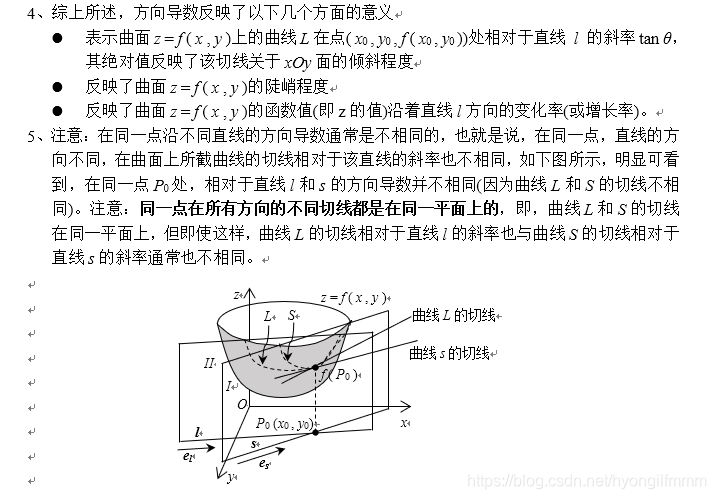
三、方向导数的计算方法及与偏导数的关系

四、梯度

8、显见，若每两条等高线的高差均相等，则在xOy面上的等高线越密的地方所对应的那部分曲线就越陡，由上面的图示可见，这是很明显的。

本文作者：黄邦勇帅(原名：黄勇) 2020-03-19