最小绝对偏差 (Least Absolute Deviations, LAD) 与最小二乘法(假设误差服从高斯分布)类似:当假设线性回归的误差服从拉普拉斯分布时,最小绝对偏差回归是对参数的最大似然估计。
问题描述
min
x
∣
∣
W
x
−
y
∣
∣
1
\min_{x} \quad || Wx-y||_1
xmin∣∣Wx−y∣∣1
等价于
min
ν
s
.
t
.
ν
=
∣
∣
W
x
−
y
∣
∣
1
\begin{array}{ll} \min & \nu \\ s.t. & \nu = || Wx-y||_1 \end{array}
mins.t.νν=∣∣Wx−y∣∣1
等价于
min
ν
s
.
t
.
∣
∣
W
x
−
y
∣
∣
1
≤
ν
\begin{array}{ll} \min & \nu \\ s.t. & || Wx-y||_1 \leq \nu \end{array}
mins.t.ν∣∣Wx−y∣∣1≤ν
等价于
min
ν
s
.
t
.
W
x
−
y
≤
ν
,
−
W
x
+
y
≤
ν
,
\begin{array}{ll} \min & \nu \\ s.t. & Wx-y \leq \nu, \\ & -Wx+y \leq \nu, \end{array}
mins.t.νWx−y≤ν,−Wx+y≤ν,
即
min
ν
s
.
t
.
W
x
−
ν
≤
y
,
−
W
x
−
ν
≤
−
y
,
\begin{array}{ll} \min & \nu \\ s.t. & Wx-\nu \leq y, \\ & -Wx -\nu \leq -y, \end{array}
mins.t.νWx−ν≤y,−Wx−ν≤−y,
即
min
[
0
I
]
⊤
[
x
ν
]
s
.
t
.
[
W
−
I
−
W
−
I
]
[
x
ν
]
≤
[
y
−
y
]
\begin{array}{ll} \min & \left[\begin{array}{ll} 0 &I\end{array}\right]^\top \left[\begin{array}{ll} x \\ \nu \end{array}\right] \\\\ s.t. & \left[\begin{array}{cc} W & -I \\ -W & -I\end{array}\right] \left[\begin{array}{c} x \\ \nu\end{array}\right] \leq \left[\begin{array}{c} y \\ -y\end{array}\right] \end{array}
mins.t.[0I]⊤[xν][W−W−I−I][xν]≤[y−y]
可见,该问题可以转化成标准的线性规划问题!!!
cvxopt 求解器
#Sources: http://cvxopt.org/examples/mlbook/l1.html?highlight=l1
from cvxopt import blas, lapack, solvers
from cvxopt import matrix, spdiag, mul, div, sparse
from cvxopt import spmatrix, sqrt, base
def l1(P, q):
P,q = matrix(P), matrix(q)
m, n = P.size
c = matrix(n*[0.0] + m*[1.0])
h = matrix([q, -q])
def Fi(x, y, alpha = 1.0, beta = 0.0, trans = 'N'):
if trans == 'N':
u = P*x[:n]
y[:m] = alpha * ( u - x[n:]) + beta*y[:m]
y[m:] = alpha * (-u - x[n:]) + beta*y[m:]
else:
y[:n] = alpha * P.T * (x[:m] - x[m:]) + beta*y[:n]
y[n:] = -alpha * (x[:m] + x[m:]) + beta*y[n:]
def Fkkt(W):
d1, d2 = W['d'][:m], W['d'][m:]
D = 4*(d1**2 + d2**2)**-1
A = P.T * spdiag(D) * P
lapack.potrf(A)
def f(x, y, z):
x[:n] += P.T * ( mul( div(d2**2 - d1**2, d1**2 + d2**2), x[n:])
+ mul( .5*D, z[:m]-z[m:] ) )
lapack.potrs(A, x)
u = P*x[:n]
x[n:] = div( x[n:] - div(z[:m], d1**2) - div(z[m:], d2**2) +
mul(d1**-2 - d2**-2, u), d1**-2 + d2**-2 )
z[:m] = div(u-x[n:]-z[:m], d1)
z[m:] = div(-u-x[n:]-z[m:], d2)
return f
uls = +q
lapack.gels(+P, uls)
rls = P*uls[:n] - q
x0 = matrix( [uls[:n], 1.1*abs(rls)] )
s0 = +h
Fi(x0, s0, alpha=-1, beta=1)
if max(abs(rls)) > 1e-10:
w = .9/max(abs(rls)) * rls
else:
w = matrix(0.0, (m,1))
z0 = matrix([.5*(1+w), .5*(1-w)])
dims = {'l': 2*m, 'q': [], 's': []}
s0 = np.array(s0)
s0[s0<=0]=1e-8
s0 = matrix(s0)
sol = solvers.conelp(c, Fi, h, dims, kktsolver = Fkkt,
primalstart={'x': x0, 's': s0}, dualstart={'z': z0})
return sol['x'][:n]
测试
A = np.random.random((10,10))
x = np.random.randn((10))
y = A @ x
n = np.random.laplace(0, 0.01, 10)
y += n
res = l1(A,y)
res = np.squeeze(res)
plt.subplot(1,2,1)
plt.bar(np.arange(len(res)),res, alpha=0.5)
plt.title('solution')
plt.subplot(1,2,2)
plt.bar(np.arange(len(x)),x, alpha=0.5)
plt.title('ground truth')
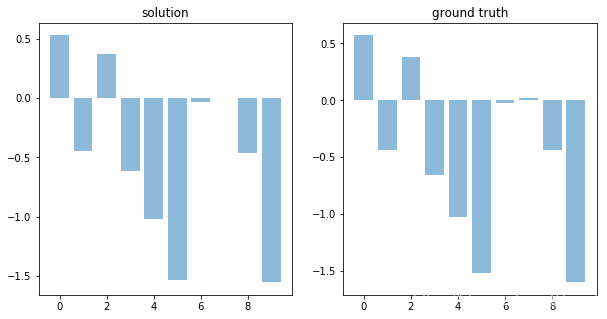



























 546
546

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?










