目录
一、标量与向量
1、标量
只有大小,没有方向的数值即称为标量。比如:长度,面积,温度等。
2、向量
又称为矢量,既有大小又有方向的量。一个向量表示一个点指向另一个点的方向和长度。向量通常可以用一个字母并在字母上加→来表示,如:
a
⃗
\vec{a}
a向量。
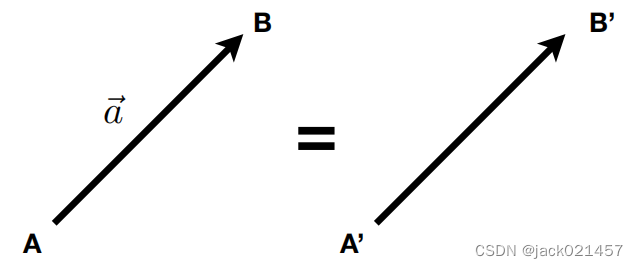
1.向量的方向
上图描述一个有 点A 指向 点B 的向量 a ⃗ \boldsymbol{\vec{a}} a 。 在同一个坐标系内,任何 a ⃗ \boldsymbol{\vec{a}} a 方向和长度相等的向量都和向量 a ⃗ \boldsymbol{\vec{a}} a 相等。比如由 点A’ 指向 点B’ 的向量 A ′ ⃗ \boldsymbol{\vec{A'}} A′ 。用向量的终点减起点即可得到这个向量的值: a ⃗ \boldsymbol{\vec{a}} a = B - A 。
2.向量的长度
向量的长度也叫向量的模,可以用两组两条|包裹的向量名来表示,如:
∣
∣
a
⃗
∣
∣
\boldsymbol{||\vec{a}||}
∣∣a∣∣ 。
还有一种比较特殊的向量叫单位向量,单位向量的意思是模长为1的向量。单位向量用向量名上面加一个尖尖的角来表示,如:
a
^
\boldsymbol{\hat{a}}
a^。 用向量除以他自己的模长即可得到他的单位向量,也叫归一化向量:
a
^
=
a
⃗
/
∣
∣
a
⃗
∣
∣
\boldsymbol{\hat{a} = \vec{a} / ||\vec{a}||}
a^=a/∣∣a∣∣ 。
在图形学中,我们关注一个方向通常都用单位向量,并不用关心它的长度
求模公式
∣
∣
A
⃗
∣
∣
=
x
2
+
y
2
||\vec{A}|| = \sqrt{x^2+y^2}
∣∣A∣∣=x2+y2
这里我们还可以理解为一个向量为列矩阵乘以他的转置矩阵。
A
⃗
=
(
x
y
)
\vec{A} = \begin{pmatrix} x \\ y \end{pmatrix}
A=(xy)
A
T
=
(
x
y
)
A^T = \begin{pmatrix}x&y\end{pmatrix}
AT=(xy)
3.向量的计算
1.向量加法
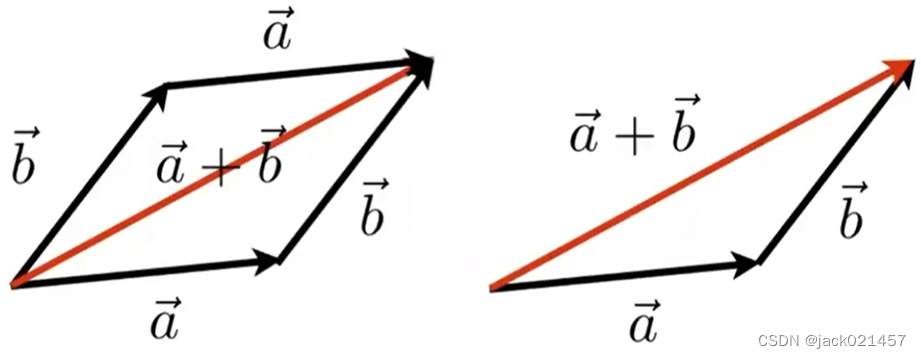
向量加法可以用两种方式来解释,分别是平行四边形法则和三角形法则。
左边的图是平行四边形法则:
两个向量合成时,以表示这两个向量的线段为邻边作平行四边形,这个平行四边形的对角线就表示合向量的大小和方向,这就叫做平行四边形定则。
这里可以这样理解:因为向量在同一平面内可以随意移动而不会改变其值,我们可以把向量
a
⃗
\boldsymbol{\vec{a}}
a和向量
b
⃗
\boldsymbol{\vec{b}}
b的起点放在一起,然后再平移另一组向量
a
⃗
\boldsymbol{\vec{a}}
a和向量
b
⃗
\boldsymbol{\vec{b}}
b使得他们围城一个平行四边形。那么这个平行四边形的对角线就是向量
a
⃗
\boldsymbol{\vec{a}}
a和向量
b
⃗
\boldsymbol{\vec{b}}
b相加之和。
右边的图是三角形法则:
把向量
a
⃗
\boldsymbol{\vec{a}}
a和向量
b
⃗
\boldsymbol{\vec{b}}
b首尾相接,从向量
a
⃗
\boldsymbol{\vec{a}}
a的起点指向向量
b
⃗
\boldsymbol{\vec{b}}
b的终点的向量就是
a
⃗
\boldsymbol{\vec{a}}
a+
b
⃗
\boldsymbol{\vec{b}}
b的结果
这个不仅适用于两个向量,也可以用于多个向量。
2.向量的减法
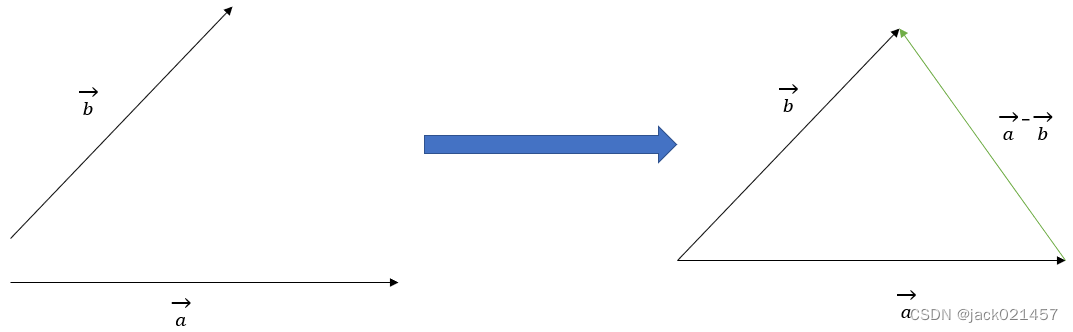
将两个向量平移至公共起点,减向量的终点指向被减向量的终点的向量即为结果。
3.向量的乘法
1.点乘
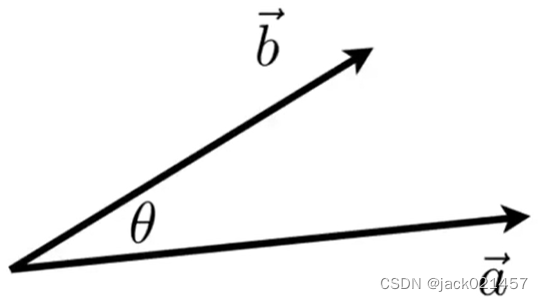
1.在图形学中我们经常使用点乘来计算两个向量的夹角,比如制作光照模型时计算光照和法线的夹角。
几何解释
a
⃗
⋅
b
⃗
=
∣
∣
a
⃗
∣
∣
∣
∣
b
⃗
∣
∣
c
o
s
θ
\boldsymbol{\vec{a} \cdot \vec{b} = ||\vec{a}|| \ ||\vec{b}|| \ cosθ}
a⋅b=∣∣a∣∣ ∣∣b∣∣ cosθ
两个向量点乘的结果是一个标量。
c
o
s
θ
=
a
⃗
⋅
b
⃗
∣
∣
a
⃗
∣
∣
∣
∣
b
⃗
∣
∣
\boldsymbol{cosθ = \frac{\vec{a} \cdot \vec{b}}{||\vec{a}|| \ ||\vec{b}||}}
cosθ=∣∣a∣∣ ∣∣b∣∣a⋅b
当两个向量都为单位向量时,公式可简化为
c
o
s
θ
=
a
^
⋅
b
^
\boldsymbol{cosθ = \hat{a} \cdot \hat{b}}
cosθ=a^⋅b^
代数解释
a
⃗
⋅
b
⃗
=
(
x
a
y
a
)
⋅
(
x
b
y
b
)
=
x
a
x
b
+
y
a
y
b
\boldsymbol{\vec{a} \cdot \vec{b} = \begin{pmatrix}x_a \\ y_a \end{pmatrix} \cdot \begin{pmatrix}x_b \\ y_b \end{pmatrix} = x_ax_b + y_ay_b}
a⋅b=(xaya)⋅(xbyb)=xaxb+yayb
a
⃗
⋅
b
⃗
=
(
x
a
y
a
z
a
)
⋅
(
x
b
y
b
z
b
)
=
x
a
x
b
+
y
a
y
b
+
z
a
z
b
\boldsymbol{\vec{a} \cdot \vec{b} = \begin{pmatrix}x_a \\ y_a \\ z_a\end{pmatrix} \cdot \begin{pmatrix}x_b \\ y_b \\ z_b \end{pmatrix} = x_ax_b + y_ay_b + z_az_b}
a⋅b=⎝
⎛xayaza⎠
⎞⋅⎝
⎛xbybzb⎠
⎞=xaxb+yayb+zazb
向量的点乘满足交换律、结合律、分配率
a
⃗
⋅
b
⃗
=
b
⃗
⋅
a
⃗
\boldsymbol{\vec{a} \cdot \vec{b} = \vec{b} \cdot \vec{a}}
a⋅b=b⋅a
a
⃗
⋅
(
b
⃗
+
c
⃗
)
=
a
⃗
⋅
b
⃗
+
a
⃗
⋅
c
⃗
\boldsymbol{\vec{a} \cdot (\vec{b}+\vec{c}) = \vec{a} \cdot \vec{b} + \vec{a}\cdot \vec{c}}
a⋅(b+c)=a⋅b+a⋅c
(
k
a
⃗
)
⋅
b
⃗
=
a
⃗
⋅
(
k
b
⃗
)
=
k
(
a
⃗
⋅
b
⃗
)
\boldsymbol{(k\vec{a}) \cdot \vec{b} = \vec{a} \cdot (k\vec{b}) = k(\vec{a} \cdot \vec{b})}
(ka)⋅b=a⋅(kb)=k(a⋅b)
如果两个向量的点乘为0则这两个向量互相垂直
a
⃗
⋅
b
⃗
=
0
\boldsymbol{\vec{a} \cdot \vec{b} = 0}
a⋅b=0
2.另外点乘还有一个作用,就是计算一个向量在另一个向量上的投影。
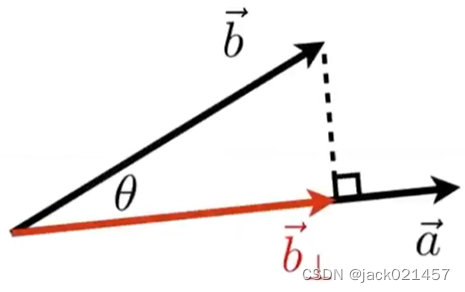
投影公式的推导过程如下
b
⃗
\boldsymbol{\vec{b}}
b在
a
⃗
\boldsymbol{\vec{a}}
a上的投影是
b
⊥
⃗
\boldsymbol{\vec{b_\perp}}
b⊥,且两个向量的夹角是θ。因为
b
⊥
⃗
\boldsymbol{\vec{b_\perp}}
b⊥是
a
⃗
\boldsymbol{\vec{a}}
a上的投影,所以
b
⊥
⃗
\boldsymbol{\vec{b_\perp}}
b⊥的方向和
a
⃗
\boldsymbol{\vec{a}}
a相同。可得:
投影值为长度d乘以单位向量
a
^
\hat{a}
a^ (1)
a
^
=
a
⃗
∣
∣
a
⃗
∣
∣
\hat{a}=\frac{\vec{a}}{||\vec{a}||}
a^=∣∣a∣∣a
b
⊥
⃗
=
d
a
⃗
∣
∣
a
⃗
∣
∣
\vec{b_\perp}=d\frac{\vec{a}}{||\vec{a}||}
b⊥=d∣∣a∣∣a
由三角函数可求出d的值 (2)
d
=
∣
∣
b
⃗
∣
∣
c
o
s
θ
d=||\vec{b}||cosθ
d=∣∣b∣∣cosθ
根据点乘公式可得 (3)
c
o
s
θ
=
a
⃗
⋅
b
⃗
∣
∣
a
⃗
∣
∣
∣
∣
b
⃗
∣
∣
cosθ = \frac{\vec{a} \cdot \vec{b}}{||\vec{a}|| \ ||\vec{b}||}
cosθ=∣∣a∣∣ ∣∣b∣∣a⋅b
投影长度:把3代入2
d
=
∣
∣
b
⃗
∣
∣
a
⃗
⋅
b
⃗
∣
∣
a
⃗
∣
∣
∣
∣
b
⃗
∣
∣
=
a
⃗
⋅
b
⃗
∣
∣
a
⃗
∣
∣
d=||\vec{b}||\frac{\vec{a} \cdot \vec{b}}{||\vec{a}|| \ ||\vec{b}||}=\frac{\vec{a} \cdot \vec{b}}{||\vec{a}||}
d=∣∣b∣∣∣∣a∣∣ ∣∣b∣∣a⋅b=∣∣a∣∣a⋅b
投影向量:把3代入2再,2再代入1,可得:
b
⊥
⃗
=
∣
∣
b
⃗
∣
∣
a
⃗
⋅
b
⃗
∣
∣
a
⃗
∣
∣
∣
∣
b
⃗
∣
∣
a
⃗
∣
∣
a
⃗
∣
∣
=
a
⃗
⋅
b
⃗
∣
∣
a
⃗
∣
∣
2
a
⃗
\vec{b_\perp}=||\vec{b}||\frac{\vec{a} \cdot \vec{b}}{||\vec{a}|| \ ||\vec{b}||}\frac{\vec{a}}{||\vec{a}||}=\frac{\vec{a} \cdot \vec{b}}{||\vec{a}||^2}\vec{a}
b⊥=∣∣b∣∣∣∣a∣∣ ∣∣b∣∣a⋅b∣∣a∣∣a=∣∣a∣∣2a⋅ba
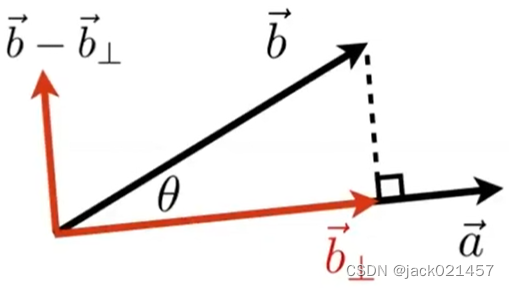
得到向量
b
⃗
\vec{b}
b在向量
a
⃗
\vec{a}
a上的投影向量后,我们可根据向量减法求出另一条直角边所代表的的向量
b
⃗
−
b
⃗
⊥
\vec{b}-\vec{b}_\perp
b−b⊥
3.通过点乘我们可以知道两个向量的是否指向同一方向

这里
a
⃗
\vec{a}
a和
b
⃗
\vec{b}
b的点乘结果大于0,我们可知他们方向基本上是一致的。
a
⃗
\vec{a}
a和
c
⃗
\vec{c}
c的点乘结果小于0则他们方向相反。如果点乘结果等于0则两个向量垂直。
4.我们可以通过点乘计算两个向量有多么接近
参考3。如果 a ⃗ \vec{a} a和 b ⃗ \vec{b} b的点乘结果越接近1,则两个向越接近。越接近-1则两个向量越远离
2.叉乘

几何解释
不同于点乘的结果是一个标量,叉乘的结果是一个向量。该向量同时垂直于两个相乘的向量所定义的平面。因为是一个向量所以有两个属性:一个是模长,一个是方向。模长的计算公式为:
∣
∣
a
⃗
×
b
⃗
∣
∣
=
∣
∣
a
⃗
∣
∣
∣
∣
b
⃗
∣
∣
s
i
n
θ
||\vec{a} \times \vec{b}|| = ||\vec{a}||||\vec{b}||sinθ
∣∣a×b∣∣=∣∣a∣∣∣∣b∣∣sinθ
方向则是由两个乘数决定的,根据右手螺旋定则,由乘数指向被乘数,拇指的方向即为叉乘结果的方向
1.作用主要用于方便我们建立一个三维空间的直角坐标系。
代数解释
a
⃗
×
b
⃗
=
(
y
a
z
b
−
y
b
z
a
z
a
x
b
−
x
a
z
b
x
a
y
b
−
y
a
x
b
)
\boldsymbol{\vec{a} \times \vec{b} = \begin{pmatrix} y_az_b-y_bz_a \\ z_ax_b-x_az_b \\ x_ay_b-y_ax_b \end{pmatrix}}
a×b=⎝
⎛yazb−ybzazaxb−xazbxayb−yaxb⎠
⎞
另一种算法是把
a
⃗
\vec{a}
a写成矩阵的形式A
a
⃗
×
b
⃗
=
A
∗
b
=
(
0
−
z
a
y
a
z
a
0
−
x
a
−
y
a
x
a
0
)
(
x
b
y
b
z
b
)
\boldsymbol{\vec{a} \times \vec{b} = A*b= \begin{pmatrix} 0 & -z_a & y_a \\ z_a & 0 & -x_a \\ -y_a & x_a & 0 \end{pmatrix} \begin{pmatrix} x_b\\ y_b\\ z_b \end{pmatrix}}
a×b=A∗b=⎝
⎛0za−ya−za0xaya−xa0⎠
⎞⎝
⎛xbybzb⎠
⎞
向量的叉乘不满足交换律:
a
⃗
×
b
⃗
=
−
b
⃗
×
a
⃗
\vec{a} \times \vec{b} = -\vec{b} \times \vec{a}
a×b=−b×a
一个向量和它自己的叉乘是
0
⃗
\vec{0}
0:
a
⃗
×
a
⃗
=
0
⃗
\vec{a} \times \vec{a} = \vec{0}
a×a=0。因为一个向量与它自己的夹角是0,所以sinθ=0.
a
⃗
×
(
b
⃗
+
c
⃗
)
=
a
⃗
×
b
⃗
+
a
⃗
×
c
⃗
\vec{a} \times (\vec{b} + \vec{c}) = \vec{a} \times \vec{b} + \vec{a} \times \vec{c}
a×(b+c)=a×b+a×c
a
⃗
×
(
k
b
⃗
)
=
k
(
a
⃗
×
b
⃗
)
\vec{a} \times (k \vec{b}) = k( \vec{a} \times \vec{b})
a×(kb)=k(a×b)
2.第二个作用:判断一个向量在另一个向量的左还是右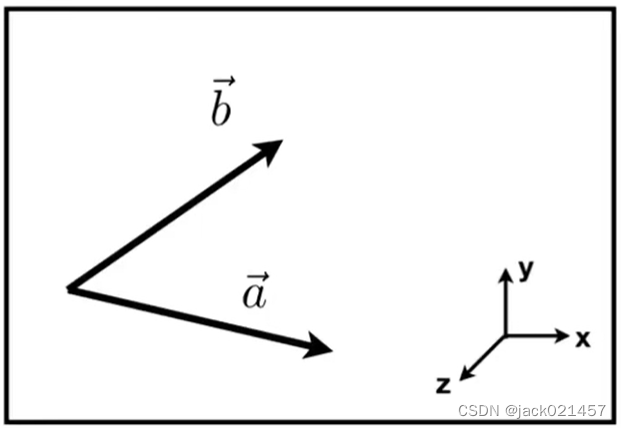
根据右手螺旋定则,如果 a ⃗ \vec{a} a和 b ⃗ \vec{b} b在xy平面内,他们两个的的叉乘结果如果是正值则证明 b ⃗ \vec{b} b在 a ⃗ \vec{a} a的左侧,反之 b ⃗ \vec{b} b在 a ⃗ \vec{a} a的右侧。
3.第三个作用:判断内外
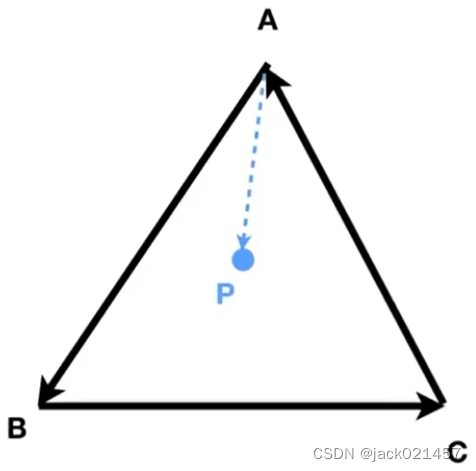
分别用
A
B
⃗
×
A
P
⃗
\vec{AB}\times\vec{AP}
AB×AP、
B
C
⃗
×
B
P
⃗
\vec{BC}\times\vec{BP}
BC×BP、
C
A
⃗
×
C
P
⃗
\vec{CA}\times\vec{CP}
CA×CP得出每次P点都在左侧,即为在该区域内部
3.点乘和叉乘的共同应用:把一个向量分解到一个三维直角坐标系上
我们可以定义一个uvw的坐标系
∣
∣
u
⃗
∣
∣
=
∣
∣
v
⃗
∣
∣
=
∣
∣
w
⃗
∣
∣
=
1
||\vec{u}||=||\vec{v}||=||\vec{w}||=1
∣∣u∣∣=∣∣v∣∣=∣∣w∣∣=1他们三个长度都为1,即为单位向量
u
⃗
⋅
v
⃗
=
v
⃗
⋅
w
⃗
=
u
⃗
⋅
w
⃗
=
0
\vec{u}\cdot\vec{v}=\vec{v}\cdot\vec{w}=\vec{u}\cdot\vec{w} = 0
u⋅v=v⋅w=u⋅w=0三个向量互相垂直
w
⃗
=
u
⃗
×
v
⃗
\vec{w}=\vec{u}\times\vec{v}
w=u×v叉乘结果等于第三个向量
这样我们就可以得到一个右手的三维直角坐标系。
然后我们把一个向量通过投影分解到这个直角坐标系上。
p
⃗
=
(
p
⃗
⋅
u
⃗
)
u
⃗
+
(
p
⃗
⋅
v
⃗
)
v
⃗
+
(
p
⃗
⋅
w
⃗
)
w
⃗
\vec{p}=(\vec{p}\cdot\vec{u})\vec{u}+(\vec{p}\cdot\vec{v})\vec{v}+(\vec{p}\cdot\vec{w})\vec{w}
p=(p⋅u)u+(p⋅v)v+(p⋅w)w
投影公式为两个向量的点乘,因为被投的向量是单位向量所以:
在u方向上的投影向量为:
∣
∣
p
⃗
∣
∣
c
o
s
θ
u
⃗
||\vec{p}|| \ cosθ \ \vec{u}
∣∣p∣∣ cosθ u
以此类推可以得到三个方向上的投影向量。即为分解之前的向量




















 845
845











 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








