永磁同步电机无感FOC滑膜观测器（SMO）

写在前面：本人能力、时间、技术有限，没有对一些细节进行深入研究和分析，也难免有不足和错误之处，欢迎交流和指正。本人写博客主要是学习过程的记录。

1、前言

滑模变结构控制是进行非线性系统分析与设计的一类普遍的方法，最早由前苏联学者 Vadim Utkin 提出，该方法能够实现系统降阶，同时具有对系统建模不确定性、外部扰动鲁棒性强，易于工程实现的优点。滑模变结构控制方法 是一种特殊的非线性控制，它能够迫使系统按照人为设定的“滑动模态”运动， 且该滑动模态的运动方程仅取决于所选择的切换函数，与系统无关。然而， 由于惯性原因，滑模变结构控制系统不可避免的出现抖振问题，如何有效削弱抖振现象成为当前的研究热点。

2、滑膜变结构基本原理

通常滑膜运动包括两部分：第一部分为趋近运动阶段；第二部分为滑膜态运动阶段。。趋近过程是从系统任意初始状态趋向滑模面，直到有限次地穿越滑模切换面的过程；滑动过程是系统状态在滑模面上趋向平衡点运动的过程。

3、传统二阶滑模观测器原理分析

4、全阶滑膜观测器原理分析

5、传统二阶滑膜控制器基于反正切的转子位置估计

6、 基于正交锁相环位置观测

7、全阶滑膜观测器仿真

PMSM全阶滑膜观测器控制框图如下图所示：

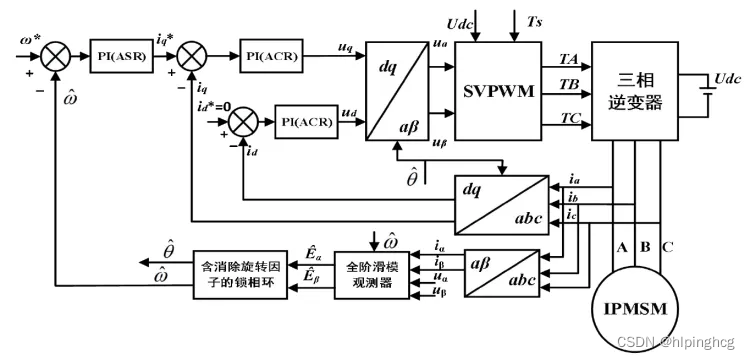
其中含消除旋转因子的锁相环如下图所示：

7.1 电机及系统参数

Ts=0.0001;
Pn=4;
Rs=0.055;
Ls=0.21e-3;
flux=0.007797;
J=0.053e-4;
B=0;
fx=0;
Udc=24;
CurrKp=0.34558;
CurrKi=90.5078;
spd_kp=0.018643;
spd_ki=03.0679;

7.2 全阶滑膜观测器核心模块

模型下载地址：永磁同步电机无感FOC滑膜观测器（SMO）simulink仿真模型

FULL_SMO+PLL内部封装：

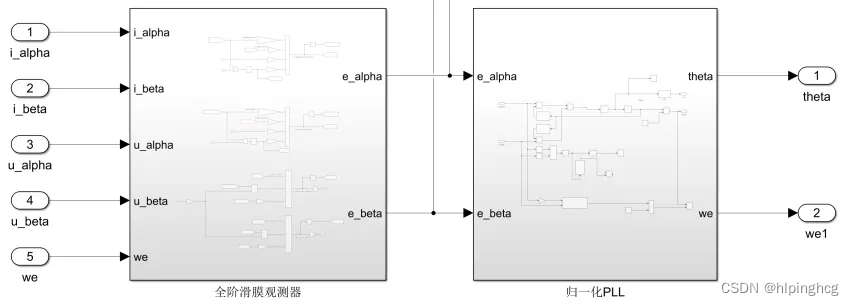
全阶滑膜观测器子模块：


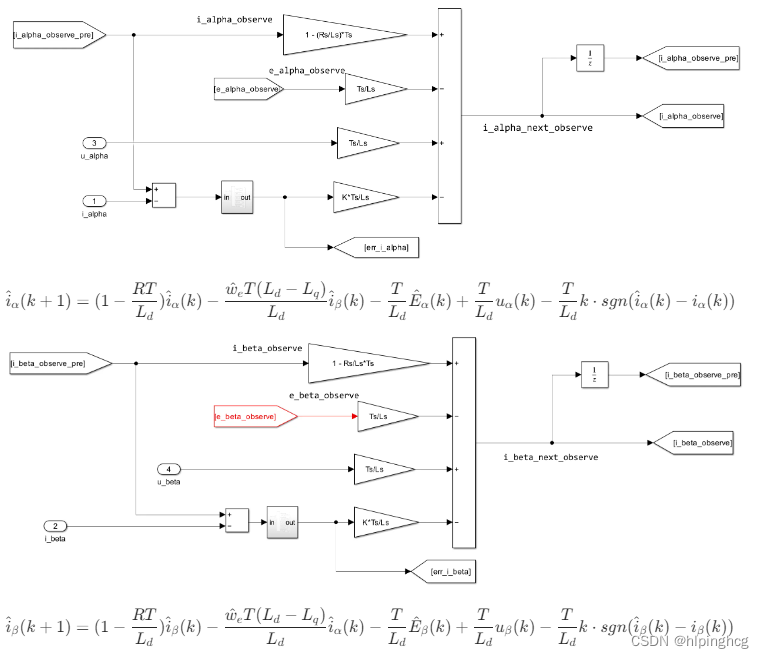
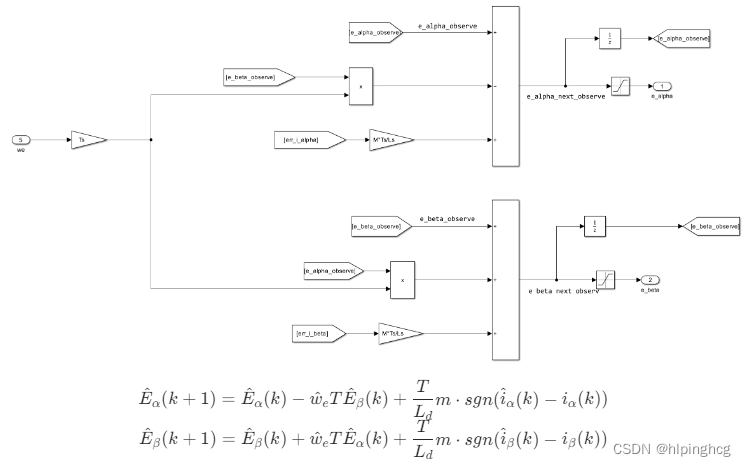
其中符号函数切换模块：


锁相环模块

7.3 仿真效果

双曲正切函数tanh函数

sign和sat函数

角度波形（观测角度及反馈角度）

总结：不同的函数有不同的效果，速度太低会出现振荡效果。

参考

参考
【1】张国强. 基于全阶滑模观测器的IPMSM无位置传感器控制策略研究[D].哈尔滨工业大学,2014.
【2】孙元杰. 基于全阶滑模观测器的IPMSM无位置传感器控制策略研究[D].曲阜师范大学,2022.DOI:10.27267/d.cnki.gqfsu.2021.001173.
【3】彻底吃透滑模观测器（PMSM无感算法）（理论精讲+推导+算法+调参+硬件运行）：
https://zhuanlan.zhihu.com/p/416224632
【4】整体撸一遍PMSM的滑模观测器（SMO）公式+模型+代码：
https://blog.csdn.net/sy243772901/article/details/131270372
【5】现代永磁同步电机控制原理及MATLAB仿真 袁雷