Qwen3 强化训练基石：GSPO 序列级强化学习算法

文章优先发布在微信公众号——“LLM大模型”，有些文章未来得及同步，可以直接关注公众号查看

---

一. 动机

近年来，强化学习（RL）已成为提升大语言模型（LLMs）推理能力的核心范式，尤其在数学推理、代码生成等复杂任务中展现出巨大潜力。

然而，随着模型规模（尤其是MoE架构）和响应长度的持续增长，现有RL算法在训练稳定性、效率与可扩展性方面面临严峻挑战。

当前主流方法如 GRPO 虽在无需价值函数估计方面取得进展，但在大规模、长序列训练中暴露出根本性缺陷：

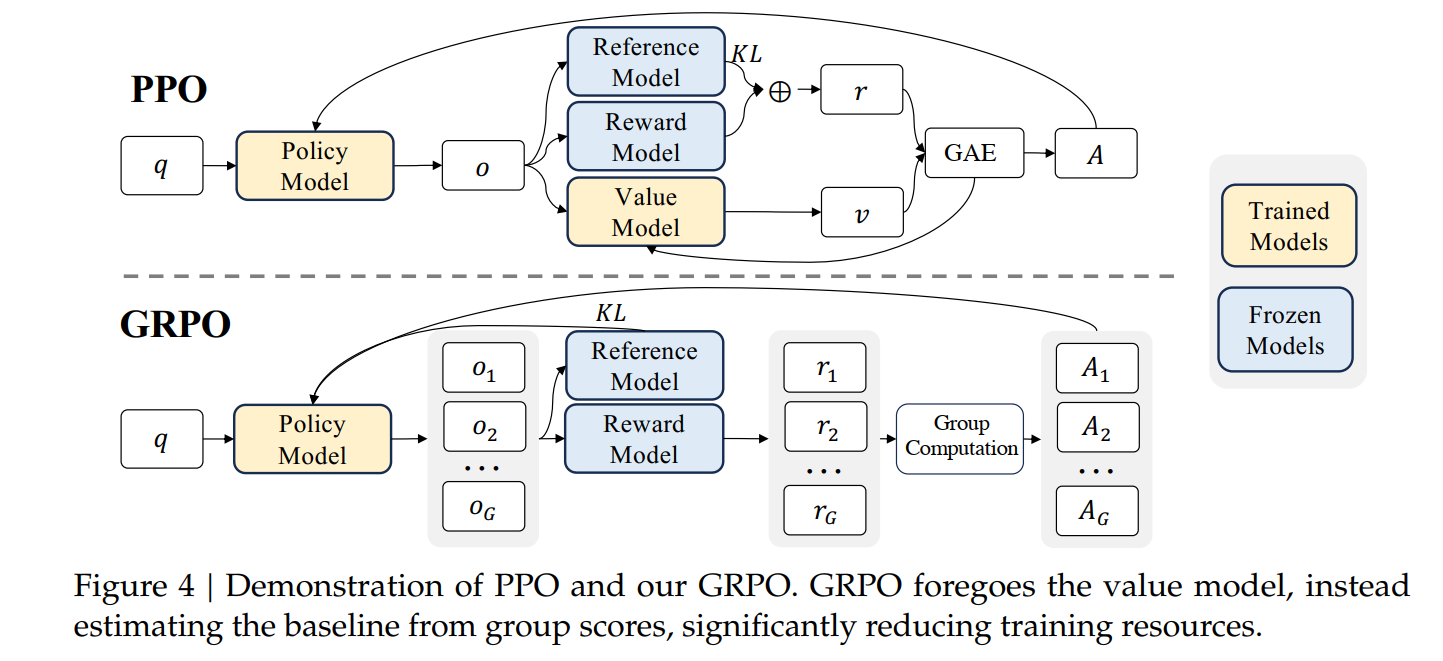
GRPO采用词元级（token-level）重要性采样权重，与序列级奖励信号不匹配，导致梯度估计方差高、训练动态不稳定，甚至引发不可逆的模型崩溃（model collapse）。

为此，Qwen团队提出 Group Sequence Policy Optimization（GSPO），一种序列级（sequence-level）的策略优化算法。不同于过去的 RL 算法，GSPO 定义了序列级别的重要性比率，并在序列层面执行裁剪、奖励和优化。相较于 GRPO，GSPO 在以下方面展现出突出优势：

• 强大高效： GSPO 具备显著更高的训练效率，并且能够通过增加计算获得持续的性能提升；

• 稳定性出色： GSPO 能够保持稳定的训练过程，并且根本地解决了混合专家（MoE）模型的 RL 训练稳定性问题；

• 基础设施友好： 由于在序列层面执行优化，GSPO 原则上对精度容忍度更高，具有简化 RL 基础设施的诱人前景。

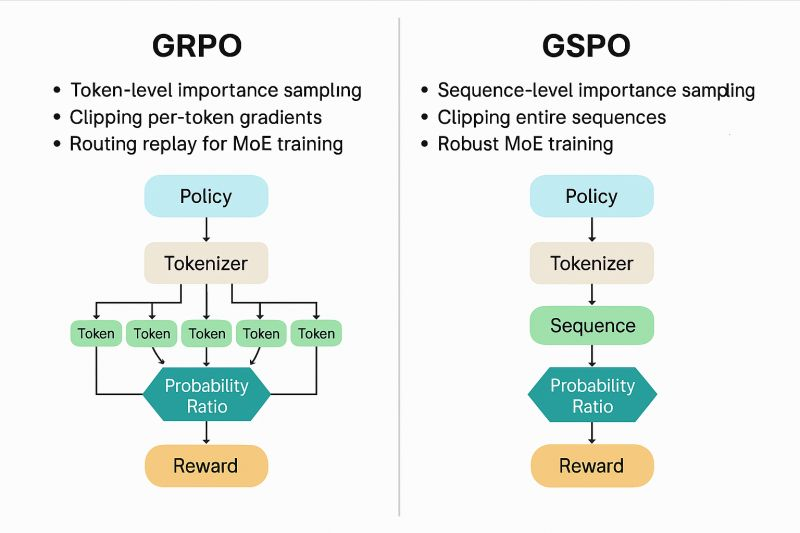
GSPO严格遵循重要性采样的理论基础，将优化目标、奖励分配与重要性权重统一于完整响应序列层面，显著提升了训练稳定性、效率与可扩展性，并成功应用于 最新 Qwen3（Instruct、Coder、Thinking）系列 模型的强化学习训练。

---

二. 现有方法回顾

2.1 基础设定与符号约定

• 策略模型：自回归语言模型 ${\pi }_{\theta }$，参数为 $\theta$。

• 查询-响应对：给定查询 $x$，模型生成响应 $y=(y_1,y_2,\dots ,y_{|y|})$，其中 $|y|$ 为响应长度。

• 响应似然：
  $${\pi }_{\theta }(y\mid x)=\prod _{t=1}^{|y|}{\pi }_{\theta }(y_t\mid x,y_{<t})$$

• 奖励函数：由外部验证器 $r$ 给出标量奖励 $r(x,y)\in [0,1]$。

2.2 PPO

PPO 通过裁剪机制约束策略更新幅度，其目标函数为：
$$J_{\text{PPO}}(\theta )={\mathbb{E}}_{x\sim \mathcal{D},y\sim {\pi }_{{\theta }_{\text{old}}}(\cdot \mid x)}\left[\frac{1}{|y|}\sum _{t=1}^{|y|}\min \left(w_t(\theta ){\hat{A}}_t,\text{clip}\left(w_t(\theta ),1-\epsilon ,1+\epsilon \right){\hat{A}}_t\right)\right]$$
其中：

• 词元级重要性比：$w_t(\theta )=\frac{{\pi }_{\theta }(y_t\mid x,y_{<t})}{{\pi }_{{\theta }_{\text{old}}}(y_t\mid x,y_{<t})}$
• ${\hat{A}}_t$ 为基于价值函数估计的优势函数。

局限：依赖高精度价值函数，计算开销大，难以扩展至长序列任务。

2.3 GRPO

GRPO 通过组内相对优势消除对价值函数的依赖：

JGRPO(θ)=Ex∼D, {yi}i=1G∼πθold(⋅∣x)[1G∑i=1G1∣yi∣∑t=1∣yi∣min⁡(wi,t(θ)A^i, clip(wi,t(θ),1−ε,1+ε)A^i)] J_{\text{GRPO}}(\theta) = \mathbb{E}_{x \sim \mathcal{D},\, \{y_i\}_{i=1}^G \sim \pi_{\theta_{\text{old}}}(\cdot \mid x)} \left[\frac{1}{G} \sum_{i=1}^{G} \frac{1}{|y_i|} \sum_{t=1}^{|y_i|} \min\left(w_{i,t}(\theta) \hat{A}_i,\,\text{clip}\left(w_{i,t}(\theta), 1 - \varepsilon, 1 + \varepsilon\right) \hat{A}_i \right) \right] JGRPO​(θ)=Ex∼D,{yi​}i=1G​∼πθold​​(⋅∣x)​​G1​i=1∑G​∣yi​∣1​t=1∑∣yi​∣​min(wi,t​(θ)A^i​,clip(wi,t​(θ),1−ε,1+ε)A^i​)​

其中：

• $w_{i,t}(\theta )=\frac{{\pi }_{\theta }(y_{i,t}\mid x,y_{i,<t})}{{\pi }_{{\theta }_{\text{old}}}(y_{i,t}\mid x,y_{i,<t})}$
• ${\hat{A}}_i=\frac{r(x,y_i)-{\mu }_r}{{\sigma }_r}$，${\mu }_r,{\sigma }_r$ 为组内奖励均值与标准差。

核心问题：词元级重要性比 $w_{i,t}(\theta )$ 基于单一样本估计，无法有效校正分布偏移，导致高方差梯度，尤其在长序列与MoE模型中加剧不稳定。

---

三. GSPO：核心思想与算法设计

3.1 理论动机：重要性采样的正确应用

重要性采样理论要求：
$${\mathbb{E}}_{z\sim {\pi }_{\text{tar}}}[f(z)]={\mathbb{E}}_{z\sim {\pi }_{\text{beh}}}\left[\frac{{\pi }_{\text{tar}}(z)}{{\pi }_{\text{beh}}(z)}f(z)\right]$$
该等式在多次采样平均下才有效。GRPO 在每个词元位置使用单一样本计算权重，违背该前提。

关键洞察：奖励作用于整个序列，因此优化单元应与奖励单元一致——即序列级。

3.2 序列级重要性比定义

GSPO 定义序列级重要性比为：
$$s_i(\theta )={\left(\frac{{\pi }_{\theta }(y_i\mid x)}{{\pi }_{{\theta }_{\text{old}}}(y_i\mid x)}\right)}^{1/|y_i|}=\exp \left(\frac{1}{|y_i|}\sum _{t=1}^{|y_i|}\log \frac{{\pi }_{\theta }(y_{i,t}\mid x,y_{i,<t})}{{\pi }_{{\theta }_{\text{old}}}(y_{i,t}\mid x,y_{i,<t})}\right)$$
长度归一化（Length Normalization）至关重要：

• 控制 $s_i(\theta )$ 数值范围，避免长序列似然指数级放大；
• 使不同长度响应的重要性比具有可比性；
• 降低方差，提升训练稳定性。

3.3 GSPO 目标函数

GSPO 采用序列级目标函数：
JGSPO(θ)=Ex∼D, {yi}i=1G∼πθold(⋅∣x)[1G∑i=1Gmin⁡(si(θ)A^i, clip(si(θ),1−ε,1+ε)A^i)] J_{\text{GSPO}}(\theta) = \mathbb{E}_{x \sim \mathcal{D},\, \{y_i\}_{i=1}^G \sim \pi_{\theta_{\text{old}}}(\cdot \mid x)} \left[ \frac{1}{G} \sum_{i=1}^{G} \min\left( s_i(\theta) \hat{A}_i,\, \text{clip}\left(s_i(\theta), 1 - \varepsilon, 1 + \varepsilon\right) \hat{A}_i \right) \right] JGSPO​(θ)=Ex∼D,{yi​}i=1G​∼πθold​​(⋅∣x)​[G1​i=1∑G​min(si​(θ)A^i​,clip(si​(θ),1−ε,1+ε)A^i​)]
其中 ${\hat{A}}_i$ 与 GRPO 相同，基于组内奖励标准化。

裁剪机制：对整个响应序列裁剪，而非逐词元裁剪，确保“过度离策略”样本被整体排除。

3.4 梯度分析：稳定性来源

GSPO 梯度（忽略裁剪）为：
$${\nabla }_{\theta }{J}_{\text{GSPO}}(\theta )=\mathbb{E}\left[\frac{1}{G}\sum _{i=1}^G{s}_i(\theta ){\hat{A}}_i\cdot {\nabla }_{\theta }\log s_i(\theta )\right]=\mathbb{E}\left[\frac{1}{G}\sum _{i=1}^G{\left(\frac{{\pi }_{\theta }(y_i\mid x)}{{\pi }_{{\theta }_{\text{old}}}(y_i\mid x)}\right)}^{1/|y_i|}{\hat{A}}_i\cdot \frac{1}{|y_i|}\sum _{t=1}^{|y_i|}{\nabla }_{\theta }\log {\pi }_{\theta }(y_{i,t}\mid x,y_{i,<t})\right]$$

关键区别：GSPO 对响应内所有词元施加相同权重 ${\left(\frac{{\pi }_{\theta }(y_i\mid x)}{{\pi }_{{\theta }_{\text{old}}}(y_i\mid x)}\right)}^{1/|y_i|}\cdot \frac{{\hat{A}}_i}{|y_i|}$，而 GRPO 使用不等权重 $w_{i,t}(\theta ){\hat{A}}_i/|y_i|$。后者权重波动大，易累积误差，导致训练崩溃。

3.5 GSPO-token：支持细粒度优势的变体

对于多轮对话等需词元级优势调整的场景，GSPO 提供变体 GSPO-token：
$$J_{\text{GSPO-token}}(\theta )=\mathbb{E}\left[\frac{1}{G}\sum _{i=1}^G\frac{1}{|y_i|}\sum _{t=1}^{|y_i|}\min \left(s_{i,t}(\theta ){\hat{A}}_{i,t},\text{clip}\left(s_{i,t}(\theta ),1-\epsilon ,1+\epsilon \right){\hat{A}}_{i,t}\right)\right]$$
其中：
$$s_{i,t}(\theta )=\text{sg}[s_i(\theta )]\cdot \frac{{\pi }_{\theta }(y_{i,t}\mid x,y_{i,<t})}{\text{sg}[{\pi }_{\theta }(y_{i,t}\mid x,y_{i,<t})]}$$

• $\text{sg}[\cdot ]$ 表示梯度截断（stop-gradient），即 PyTorch 中的 .detach()；
• 数值上 $s_{i,t}(\theta )=s_i(\theta )$，但允许 ${\hat{A}}_{i,t}$ 逐词元定制；
• 梯度形式与 GSPO 一致，保持稳定性。

重要性质：当 ${\hat{A}}_{i,t}={\hat{A}}_i$（常数）时，GSPO-token 与 GSPO 完全等价。

---

四. 技术优势与实证分析

4.1 训练稳定性与效率

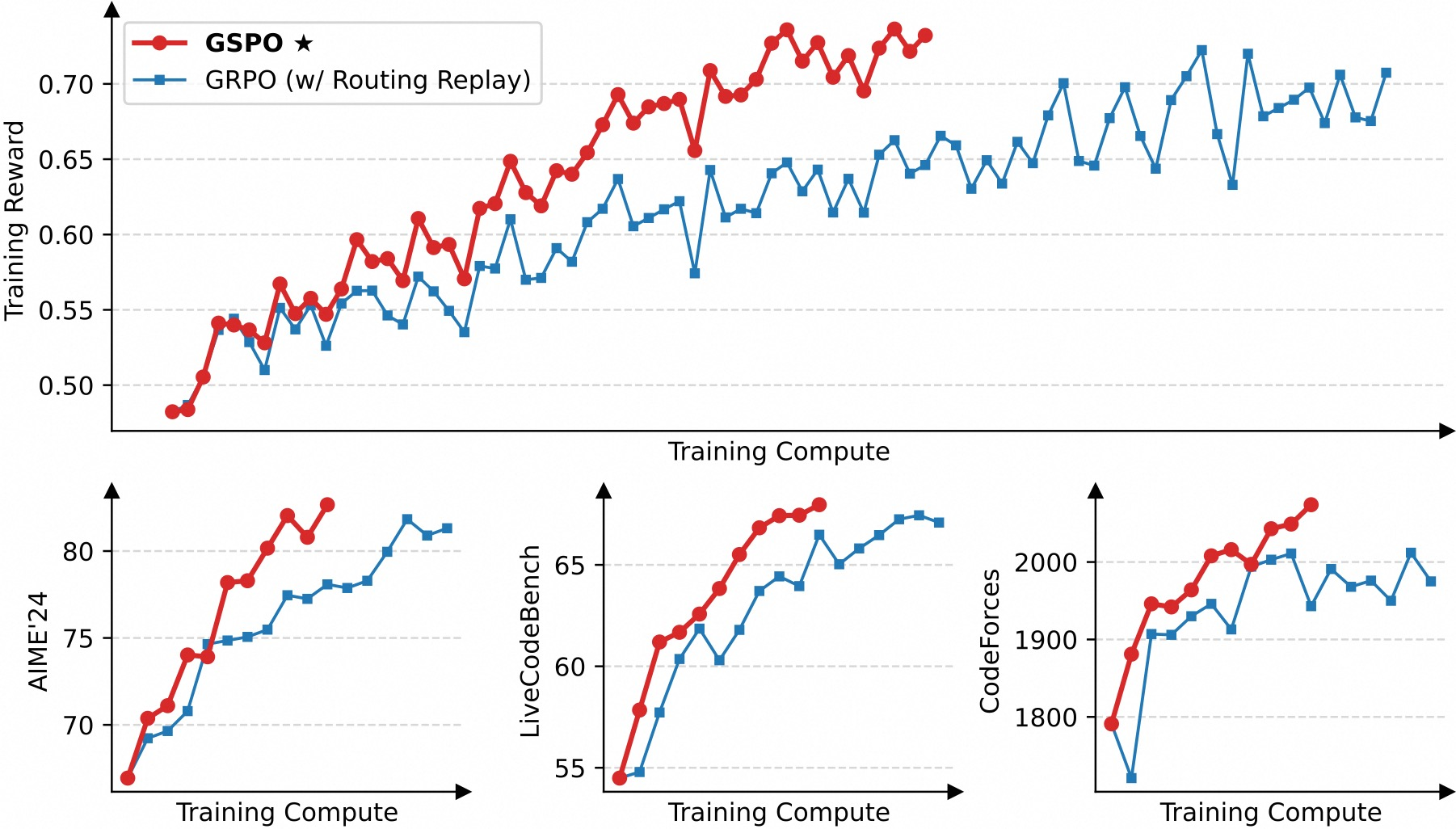
• 稳定性：GSPO 在 Qwen3-30B-A3B-Base 上实现全程稳定训练，无崩溃现象；
• 效率：相同计算量下，GSPO 在 AIME’24、LiveCodeBench、CodeForces 等基准上显著优于 GRPO；
• 可扩展性：支持持续增加训练算力、更新查询集、延长生成长度，性能持续提升。

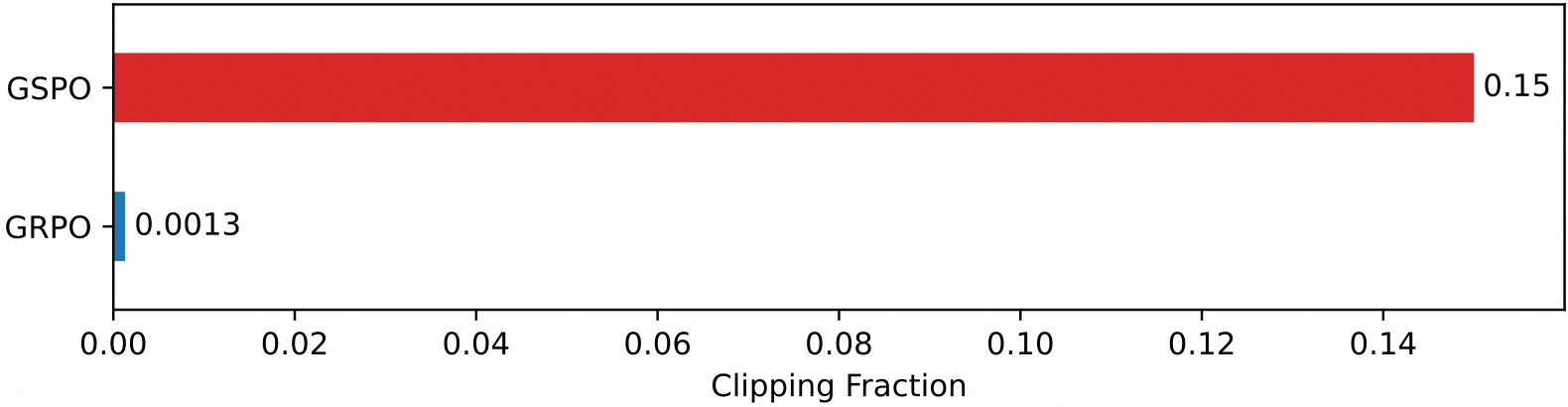
4.2 裁剪行为分析

• 裁剪比例：GSPO 裁剪整个响应，词元裁剪比例高达 ~15%；GRPO 仅 ~0.13%；
• 反直觉结论：尽管 GSPO 使用更少样本，但训练效率更高 → 证明 GRPO 词元级梯度噪声大、样本利用率低。

4.3 MoE 模型训练优势

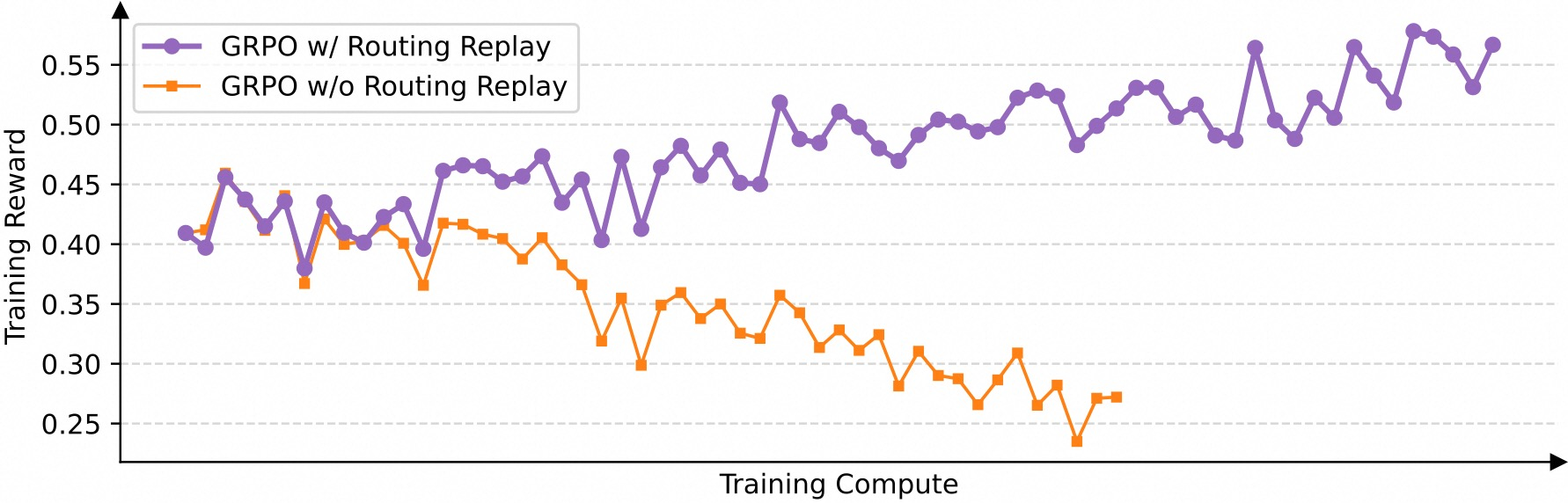
问题：MoE 模型在 RL 更新后专家激活路径剧烈变化（约10%专家切换），导致词元级似然比 $w_{i,t}(\theta )$ 失效。

GRPO 解法：需 Routing Replay —— 缓存旧策略专家路由，在新策略中强制复用，增加内存与通信开销，限制模型容量。

GSPO 解法：

• 仅依赖序列似然 ${\pi }_{\theta }(y_i\mid x)$，对内部路由不敏感；
• 序列似然在 MoE 中仍保持平滑（语言建模能力稳定）；
• 无需 Routing Replay，简化训练流程，释放模型全部容量。

4.4 RL 基础设施简化

• 问题：训练引擎（Megatron）与推理引擎（vLLM/SGLang）存在精度差异，GRPO 需用训练引擎重计算旧策略似然；
• GSPO 优势：序列级似然对精度差异鲁棒性强，可直接使用推理引擎输出的似然进行优化；
• 收益：避免重计算，适用于部分 rollout、多轮 RL、训推分离架构。

---

五. GRPO 与 GSPO 对比

特性	GRPO	GSPO
优化单元	词元级	序列级
重要性比	词元似然比	序列似然比（长度归一化）
裁剪粒度	词元	响应序列
MoE 训练	需 Routing Replay	无需额外策略
基础设施依赖	需训练引擎重计算	可直接用推理引擎似然
稳定性	易崩溃	高度稳定
样本效率	低（高方差梯度）	高

GSPO 核心贡献：

1. 理论正确性：严格遵循重要性采样原理，统一优化与奖励单元；
2. 工程实用性：解决 MoE RL 训练稳定性难题，简化基础设施；
3. 性能优越性：显著提升训练效率与最终模型性能。

GSPO 已成为 Qwen3 系列模型强化学习训练的算法基石，为未来超大规模语言模型的 RL 扩展提供了可靠、高效、可扩展的技术路径。