通俗易懂地理解卷积

作者：palet
链接：https://www.zhihu.com/question/22298352/answer/637156871
来源：知乎
著作权归作者所有。商业转载请联系作者获得授权，非商业转载请注明出处。
 

        卷积这个概念，很早以前就学过，但是一直没有搞懂。教科书上通常会给出定义，给出很多性质，也会用实例和图形进行解释，但究竟为什么要这么设计，这么计算，背后的意义是什么，往往语焉不详。作为一个学物理出身的人，一个公式倘若倘若给不出结合实际的直观的通俗的解释（也就是背后的“物理”意义），就觉得少了点什么，觉得不是真的懂了。

         ​并且也解释了，先对g函数进行翻转，相当于在数轴上把g函数从右边褶到左边去，也就是卷积的“卷”的由来。

        然后再把g函数平移到n，在这个位置对两个函数的对应点相乘，然后相加，这个过程是卷积的“积”的过程。

        这个只是从计算的方式上对公式进行了解释，从数学上讲无可挑剔，但进一步追问，为什么要先翻转再平移，这么设计有何用意？还是有点费解。

        在知乎，已经很多的热心网友对卷积举了很多形象的例子进行了解释，如卷地毯、丢骰子、打耳光、存钱等等。读完觉得非常生动有趣，但过细想想，还是感觉有些地方还是没解释清楚，甚至可能还有瑕疵，或者还可以改进（这些后面我会做一些分析）。

带着问题想了两个晚上，终于觉得有些问题想通了，所以就写出来跟网友分享，共同学习提高。不对的地方欢迎评论拍砖。。。

明确一下，这篇文章主要想解释两个问题：

1. 卷积这个名词是怎么解释？“卷”是什么意思？“积”又是什么意思？

2. 卷积背后的意义是什么，该如何解释？

考虑的应用场景

为了更好地理解这些问题，我们先给出两个典型的应用场景：

1. 信号分析

一个输入信号f(t)，经过一个线性系统（其特征可以用单位冲击响应函数g(t)描述）以后，输出信号应该是什么？实际上通过卷积运算就可以得到输出信号。

2. 图像处理

输入一幅图像f(x,y)，经过特定设计的卷积核g(x,y)进行卷积处理以后，输出图像将会得到模糊，边缘强化等各种效果。

对卷积的理解

        对卷积这个名词的理解：所谓两个函数的卷积，本质上就是先将一个函数翻转，然后进行滑动叠加。

        在连续情况下，叠加指的是对两个函数的乘积求积分，在离散情况下就是加权求和，为简单起见就统一称为叠加。

        整体看来是这么个过程：

翻转——>滑动——>叠加——>滑动——>叠加——>滑动——>叠加.....

        多次滑动得到的一系列叠加值，构成了卷积函数。

        卷积的“卷”，指的的函数的翻转，从 g(t) 变成 g(-t) 的这个过程；同时，“卷”还有滑动的意味在里面（吸取了网友李文清的建议）。如果把卷积翻译为“褶积”，那么这个“褶”字就只有翻转的含义了。

        卷积的“积”，指的是积分/加权求和。

        有些文章只强调滑动叠加求和，而没有说函数的翻转，我觉得是不全面的；有的文章对“卷”的理解其实是“积”，我觉得是张冠李戴。

        对卷积的意义的理解：

        1. 从“积”的过程可以看到，我们得到的叠加值，是个全局的概念。以信号分析为例，卷积的结果是不仅跟当前时刻输入信号的响应值有关，也跟过去所有时刻输入信号的响应都有关系，考虑了对过去的所有输入的效果的累积。在图像处理的中，卷积处理的结果，其实就是把每个像素周边的，甚至是整个图像的像素都考虑进来，对当前像素进行某种加权处理。所以说，“积”是全局概念，或者说是一种“混合”，把两个函数在时间或者空间上进行混合。

        2. 那为什么要进行“卷”？直接相乘不好吗？我的理解，进行“卷”（翻转）的目的其实是施加一种约束，它指定了在“积”的时候以什么为参照。在信号分析的场景，它指定了在哪个特定时间点的前后进行“积”，在空间分析的场景，它指定了在哪个位置的周边进行累积处理。

举例说明

下面举几个例子说明为什么要翻转，以及叠加求和的意义。

例1：信号分析

如下图所示，输入信号是 f(t) ，是随时间变化的，。系统响应函数是 g(t) ，图中的响应函数是随时间指数下降的，它的物理意义是说：如果在 t=0 的时刻有一个输入，那么随着时间的流逝，这个输入将不断衰减。换言之，到了 t=T时刻，原来在 t=0 时刻的输入f(0)的值将衰减为f(0)g(T)。

​        上述例子更简单的表述为，f是输入，其对应的输出或者响应是g(t)，而响应随着时间的变化也会发生变化，比如说，f是一个脉冲信号，输出g是脉冲信号的强度。很显然，脉冲信号的强度随着时间的变化而变化，也就是g(t)。对于任何一个单位脉冲，自它发出之后，它的信号强度随着t的变化是相同的。现在问，在多个时刻发出的脉冲，在某个具体时刻k的的脉冲信号强度是多少。这个就需要计算上述多个时刻发生的脉冲，到了k时刻的强度，然后把这些强度加起来。如果发出的脉冲是个连续或者离散的，并且每个脉冲的强度不同，那么输入也可以表示成一个随时间变化的函数。只不过f(t)表示在t时刻发出的脉冲的强度。g(t)表示在0时刻发出的单位脉冲在t时刻的强度，也就是说g(t)是f(0)/||f(0)||脉冲在t时刻的观测值或者输出。那么对于[0,t]这个时间区间内，所有发生的脉冲，在t时刻的输出的叠加就是我们想要的结果了。要分别找到f(k) 在t时刻的响应f(k)*g(t-k)的累计(因为g(t)表示的是0时刻发出的单位脉冲在不同时刻的强度值，f(k)表示k时刻发出的脉冲值，可能并不是单位脉冲)，，这里就需要遍历所有的满足条件的k了。这里之所以说单位脉冲f(k)/||f(k)||在t时刻的响应是g(t-k)而不是g(t)，就是因为g(t)是f(0)/||f(0)||脉冲在t时刻的输出，现在f(k)/||f(k)||表示的是k时刻发出的单位脉冲，其到t时刻只有t-k时间段而已，所以只能是g(t-k)。

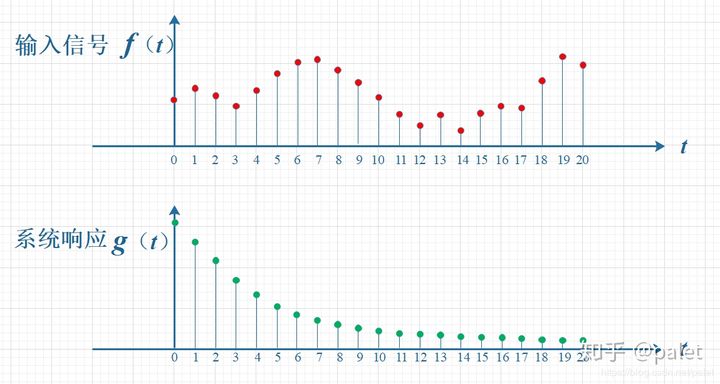
​​        考虑到信号是连续输入的，也就是说，每个时刻都有新的信号进来，所以，最终输出的是所有之前输入信号的累积效果。如下图所示，在T=10时刻，输出结果跟图中带标记的区域整体有关。其中，f(10)因为是刚输入的，所以其输出结果应该是f(10)g(0)，而时刻t=9的输入f(9)，只经过了1个时间单位的衰减，所以产生的输出应该是 f(9)g(1)，如此类推，即图中虚线所描述的关系。这些对应点相乘然后累加，就是T=10时刻的输出信号值，这个结果也是f和g两个函数在T=10时刻的卷积值。

        ​​显然，上面的对应关系看上去比较难看，是拧着的，所以，我们把g函数对折一下，变成了g(-t)，这样就好看一些了。看到了吗？这就是为什么卷积要“卷”，要翻转的原因，这是从它的物理意义中给出的。

​

​​上图虽然没有拧着，已经顺过来了，但看上去还有点错位，所以再进一步平移T个单位，就是下图。它就是本文开始给出的卷积定义的一种图形的表述：

​

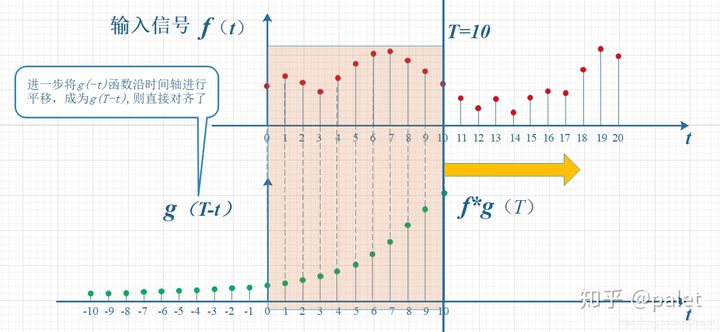
​​        所以，在以上计算T时刻的卷积时，要维持的约束就是： t+ (T-t) = T 。这种约束的意义，大家可以自己体会。

例2：丢骰子

在本问题 如何通俗易懂地解释卷积？中排名第一的 马同学在中举了一个很好的例子（下面的一些图摘自马同学的文章，在此表示感谢），用丢骰子说明了卷积的应用。

要解决的问题是：有两枚骰子，把它们都抛出去，两枚骰子点数加起来为4的概率是多少?

​

​​分析一下，两枚骰子点数加起来为4的情况有三种情况：1+3=4， 2+2=4, 3+1=4

因此，两枚骰子点数加起来为4的概率为：

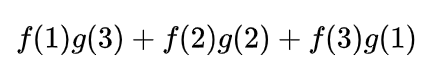
​​写成卷积的方式就是：​

​​在这里我想进一步用上面的翻转滑动叠加的逻辑进行解释。

首先，因为两个骰子的点数和是4，为了满足这个约束条件，我们还是把函数 g 翻转一下，然后阴影区域上下对应的数相乘，然后累加，相当于求自变量为4的卷积值，如下图所示：

​

​​进一步，如此翻转以后，可以方便地进行推广去求两个骰子点数和为 n 时的概率，为f 和 g的卷积 f*g(n)，如下图所示：​

​​        由上图可以看到，函数 g 的滑动，带来的是点数和的增大。这个例子中对f和g的约束条件就是点数和，它也是卷积函数的自变量。有兴趣还可以算算，如果骰子的每个点数出现的概率是均等的，那么两个骰子的点数和n=7的时候，概率最大。
 

例3：图像处理

还是引用知乎问题 如何通俗易懂地解释卷积？中 马同学的例子。图像可以表示为矩阵形式（下图摘自马同学的文章）：

对图像的处理函数（如平滑，或者边缘提取），也可以用一个g矩阵来表示，如：

        从卷积定义来看，应该是在x和y两个方向去累加（对应上面离散公式中的i和j两个下标），而且是无界的，从负无穷到正无穷。可是，真实世界都是有界的。例如，上面列举的图像处理函数g实际上是个3x3的矩阵，意味着，在除了原点附近以外，其它所有点的取值都为0。考虑到这个因素，上面的公式其实退化了，它只把坐标（u,v）附近的点选择出来做计算了。所以，真正的计算如下所示：

​​首先我们在原始图像矩阵中取出（u,v）处的矩阵：

         然后将图像处理矩阵翻转（这个翻转有点意思，可以有几种不同的理解，其效果是等效的：（1）先沿x轴翻转，再沿y轴翻转；（2）先沿x轴翻转，再沿y轴翻转；），如下：

原始矩阵：

        请注意，以上公式有一个特点，做乘法的两个对应变量a,b的下标之和都是（u,v），其目的是对这种加权求和进行一种约束。这也是为什么要将矩阵g进行翻转的原因。以上矩阵下标之所以那么写，并且进行了翻转，是为了让大家更清楚地看到跟卷积的关系。这样做的好处是便于推广，也便于理解其物理意义。实际在计算的时候，都是用翻转以后的矩阵，直接求矩阵内积就可以了。

        以上计算的是（u,v）处的卷积，延x轴或者y轴滑动，就可以求出图像中各个位置的卷积，其输出结果是处理以后的图像（即经过平滑、边缘提取等各种处理的图像）。

        再深入思考一下，在算图像卷积的时候，我们是直接在原始图像矩阵中取了（u,v）处的矩阵，为什么要取这个位置的矩阵，本质上其实是为了满足以上的约束。因为我们要算（u，v）处的卷积，而g矩阵是3x3的矩阵，要满足下标跟这个3x3矩阵的和是（u,v），只能是取原始图像中以（u，v）为中心的这个3x3矩阵，即图中的阴影区域的矩阵。

        推而广之，如果如果g矩阵不是3x3，而是7x7，那我们就要在原始图像中取以（u，v）为中心的7x7矩阵进行计算。由此可见，这种卷积就是把原始图像中的相邻像素都考虑进来，进行混合。相邻的区域范围取决于g矩阵的维度，维度越大，涉及的周边像素越多。而矩阵的设计，则决定了这种混合输出的图像跟原始图像比，究竟是模糊了，还是更锐利了。

        比如说，如下图像处理矩阵将使得图像变得更为平滑，显得更模糊，因为它联合周边像素进行了平均处理：