【吴恩达 机器学习】 逻辑回归算法Matlab实现

一，假设函数：

1） 逻辑回归（Logistic Regression)，Logistic function, Sigmoid function是同一个意思，函数形式（假设函数形式）如下:

逻辑回归是二分类算法，$h_{\theta}(x) >= 0.5$（$z >=0$, 即${\theta}^Tx >= 0$），则$y = 1$。

2） 决策边界(Decision Boundary)
逻辑函数分为正类和负类时的边界，即$h_{\theta}(x) = 0.5$即为边界函数。

上图假定参数$\theta$已经学好, 根据上一张图知${\theta}^Tx >= 0$为正类，${\theta}^Tx < 0$为负类，则边界为${\theta}^Tx = 0$，此时边界为$x_1 + x_2 = 3$

3） 非线性决策边界
假设已经使用训练集训练逻辑回归模型，得到参数$\theta$，于线性边界一样，则非线性决策边界为${\theta}^Tx = 0$，如下

二，参数学习

1) 损失函数，学习参数，首先需要定义损失函数，线性回归的损失函数可以是均方误差

$$J(\theta) = \frac{1}{m} \sum_{i=1}^{m} (h_{\theta}(x^i)-y^i)^2$$ ，但逻辑回归的损失函数不能使用均方误差函数，因为逻辑回归函数 $h_{\theta}(x) =\frac{1}{1+exp(-\theta^Tx)}$，也叫Sigmoid function作为假设函数，此函数是非线性的，会导致均方误差函数为non-convex（ 函数的二阶导数大于等于零，那么这个函数就是凸函数），有许多局部最小值。所有需要定义新的损失函数，如下：

损失函数另一种表达方式是：

$$Cost(h_{\theta}(x), y) = -y log (h_{\theta}(x)) - (1-y)log(1-h_{\theta}(x))$$
所有样本的损失值之和： $$J(\theta) = 1/m\sum_{i=1}^{m} Cost(h_{\theta}(x), y)$$

2) 使用梯度下降算法，找到$J$损失值最小时的参数$\theta$，预测某个样本$x$时，利用得到的参数$\theta$代入假设函数（逻辑回归函数，Sigmoid函数），即可求得预测值：

$$h_{\theta}(x) =\frac{1}{1+exp(-\theta^Tx)}$$

3) 梯度下降法，损失函数偏导具体推导过程参考链接：

前面已经确定了三要素：假设函数，损失函数，梯度下降

三，Matlab实现

数据集下载：百度云链接 密码：tb4p

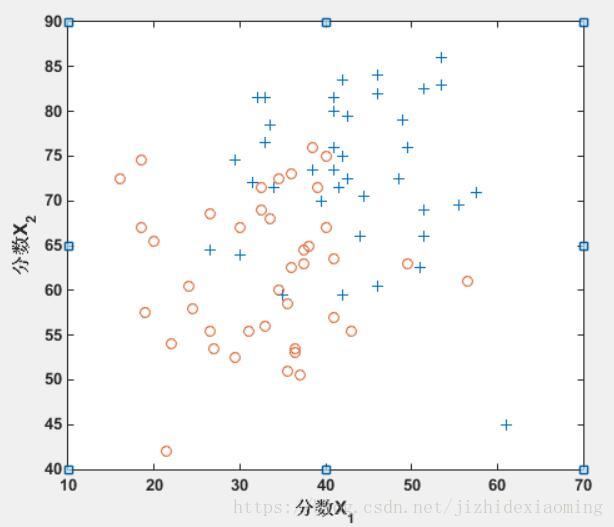
假设一所高中有一个数据集，代表40名学生被录取进入大学，40名学生未被录取。训练样本包含两个标准化考试的学生成绩和学生是否被录取的标签。

任务是建立一个二元分类模型，根据学生在两次考试中的分数来估计大学录取的机会。

ex4x.dat：X数组的第一列代表所有的测试1分数，第二列代表所有的测试2分数。
ex4y.dat：Y向量使用“1”来标记被录取和“0”以标记未录取的学生。

数据分布：

Matlab代码：

clear;
clc;
% 1，读入数据
load('D:\Code\Data\ex4Data\ex4x.dat');
load('D:\Code\Data\ex4Data\ex4y.dat');
x = ex4x;
y = ex4y;

% 2，显示数据，查看分布
pos = find(y == 1); neg = find(y == 0);
plot(x(pos, 1), x(pos,2), '+'); hold on
plot(x(neg, 1), x(neg, 2), 'o')

% 3, 参数设置
iteration = 10000;
sample_num = length(x); % 样本个数
x = [ones(sample_num, 1), x];
theta = zeros(size(x, 2), 1); % 参数
alpha = 0.1;

% 4，特征归一化
x(:,2) = (x(:,2)- mean(x(:,2)))./ std(x(:,2));
x(:,3) = (x(:,3)- mean(x(:,3)))./ std(x(:,3));

% 5，迭代，寻找最佳参数
for i = 1:iteration
    h = 1 ./ (1 + exp(-x * theta)); % 通过假设函数得到预测值
    J(i,1) = -1/sample_num * (y' * log(h+eps) + (1-y)'*log(1-h+eps)); % 当前参数下的损失值
    theta(1,1) = theta(1,1) - alpha * sum((h - y) .* x(:,1));  % 更新参数
    theta(2,1) = theta(2,1) - alpha * sum((h - y) .* x(:,2));
    theta(3,1) = theta(3,1) - alpha * sum((h - y) .* x(:,3));
    %theta = theta - alpha * x'*(h-y); % 同时更新所有参数
end

figure,
plot(x(pos, 2), x(pos,3), '+'); hold on
plot(x(neg, 2), x(neg, 3), 'o')

% 6，边界为Theta'x = 0; theta_1 + theta_2*x_2 + theta_3*x_3 = 0
max_value = max(x(:,2));
min_value = min(x(:,2));
X = min_value:0.001:max_value;
Y = -(theta(1,1) + theta(2,1) * X) / theta(3,1);
plot(X, Y, '-')

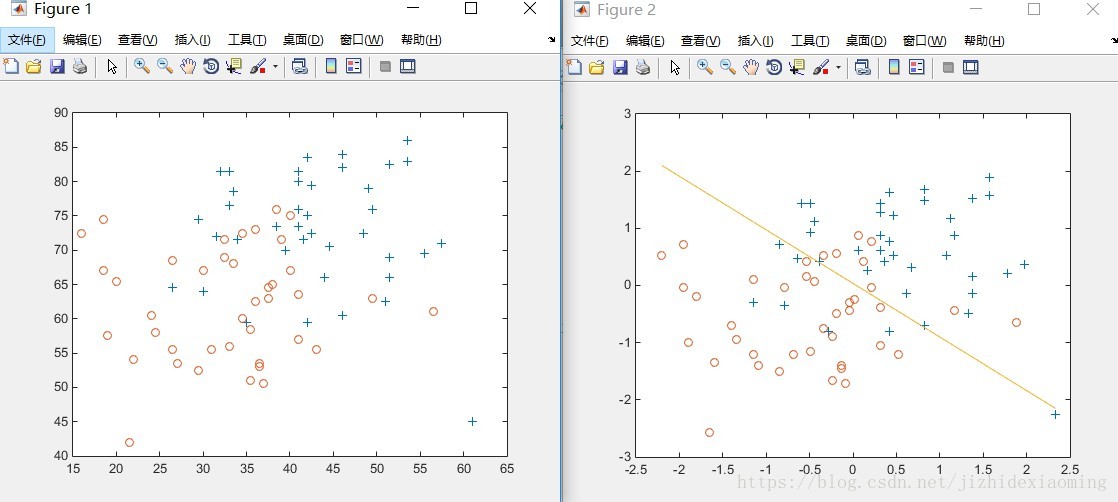
效果图，画决策边界（$h_\theta(z)=0.5, 此时z=\theta^Tx=0$）：

关键代码（向量化表示）：

theta(1,1) = theta(1,1) - alpha * sum((h - y) .* x(:,1));  % 更新参数
theta(2,1) = theta(2,1) - alpha * sum((h - y) .* x(:,2));
theta(3,1) = theta(3,1) - alpha * sum((h - y) .* x(:,3));
%theta = theta - alpha * x'*(h-y); % 同时更新所有参数