5.2.1 MATLAB学习笔记之绘图-其他形式的二维图形1

其他形式的二维图形1

二维图线除采用直角坐标系外，还可采用对数坐标或极坐标。除了绘制二维曲线外， MATLAB 的二维图形还包括各种二维统计分析图形。

一、对函数自适应采样的绘图函数

plot 函数基本的操作方法为，先取足够稠密的自变量向量x, 然后计算出函数值向量y, 最后用绘图函数绘图。在取数据点时一般都是等间隔采样，这对绘制高频率变化的函数不够精确。

例如函数f(x)=cos(tan(πx)), 在(0,1)范围有无限多个振荡周期，函数变化率大。

为提高精度，绘制出比较真实的函数曲线，就不能等间隔采样，而必须在变化率大的区段密集采样，以充分反映函数的实际变化规律，进而提高图形的真实度。

fplot 函数可自适应地对函数进行采样，能更好地反映函数的变化规律，其调用格式如下： fplot(filename,lims, 选项)

• 其中，filename 代表一个函数，通常采用函数句柄的形式，也可以是字符串形式，很多MATLAB 函数都有这种用法。可以指定多个分量函数，这时要以单元向量表示。
• lims 为 x 轴的取值范围， 取二元向量[xmin,xmax], 默认值为[-5,5]。
• 选项定义与plot 函数相同。

>>f=@sin;
>>fplot(f,[0,2*pi],'*')
>>fplot({@(x)sin(x),@(x)cos(x)},[0,2*pi],'r.')

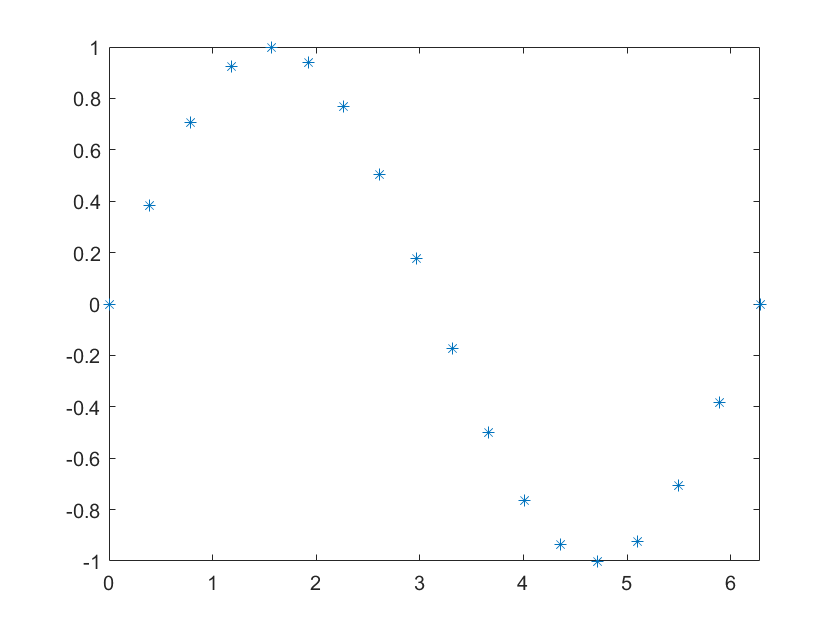
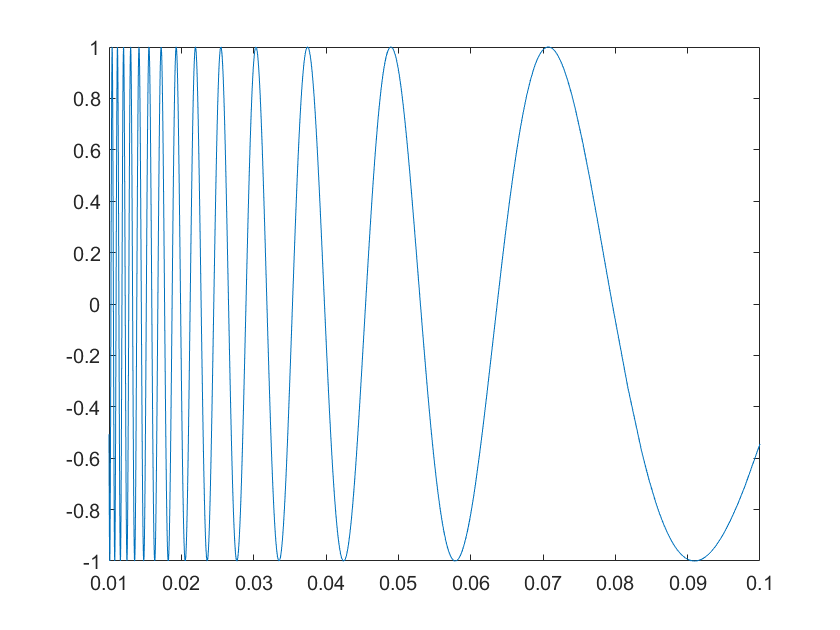
观察上述语句绘制的正、余弦曲线采样点的分布，可以发现曲线变化率大的区段，采样点 比较密集。

例1 用 fplot 函数绘制f(x)=cos(tan(πx)) 的曲线。

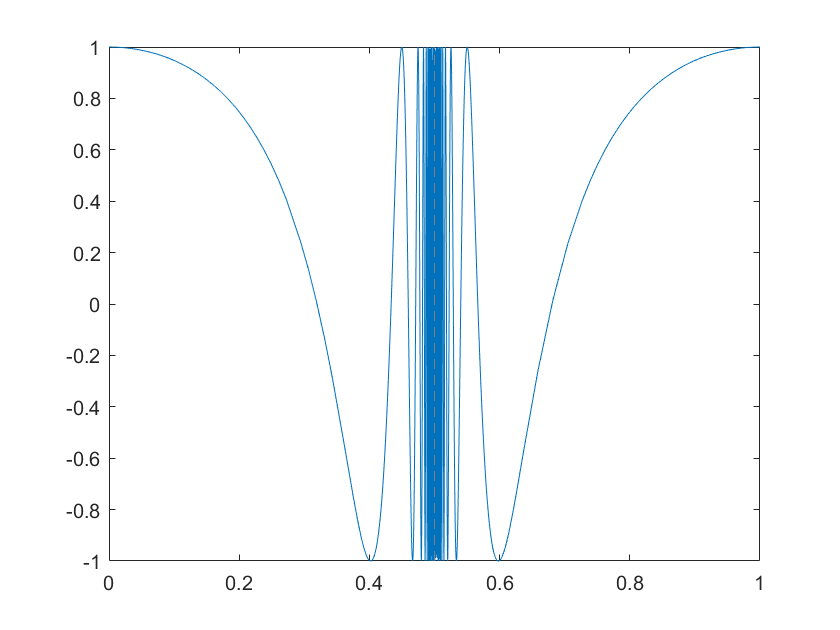
从图可以看出，在x=0.5 附近采样点十分密集。

二、其他坐标系下的二维曲线图

1.对数坐标图形

在工程应用中，经常用到对数坐标，例如自动控制理论中的 Bode 图就采用对数坐标。

MATLAB提供了绘制半对数和全对数坐标曲线的函数，调用格式如下：

semilogx(x1,y1,选项1,x2,y2, 选项2, …)

semilogy(x1,y1,选项1,×2,y2, 选项2,…)

loglog(x1,y1, 选项1,x2,y2, 选项2, …)

其中，选项的定义与plot 函数完全一致，所不同的是坐标轴的选取。

• semilogx 函数使用半对数坐标，x 轴为常用对数刻度，而y轴仍保持线性刻度。
• semilogy 函数也使用半对数坐标，y 轴为 常用对数刻度，而x 轴仍保持线性刻度。
• loglog函数使用全对数坐标，x 轴和y 轴均采用常用对数刻度。

例2 绘制y=10x²的对数坐标图并与直角线性坐标图进行比较。

x=0:0.1:10;
y=10*x.*x;
subplot(2,2,1);plot(x,y)  %直角坐标曲线
title('plot(x,y)');grid on
subplot(2,2,2);semilogx(x,y)    %x半对数坐标曲线
title('semilogx(x,y)');grid on
subplot(2,2,3);semilogy(x,y)    %y半对数坐标曲线
title('semilogy(x,y)');grid on
subplot(2,2,4);loglog(x,y)        %全对数坐标曲线
title('loglog(x,y)');grid on

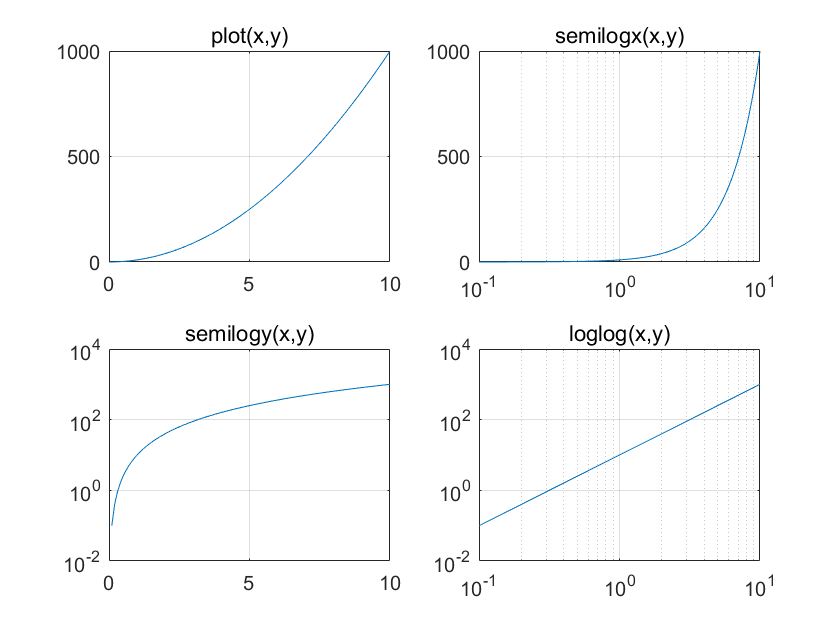
2.极坐标图

**polar**函数用来绘制极坐标图，其调用格式如下：

polar(theta,rho, 选项)

其中，theta 为极坐标极角，rho 为极坐标极径，选项的内容与plot函数相似。

例3 蝴蝶曲线是一种富有美感的平面曲线，其极坐标方程如下：

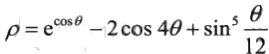
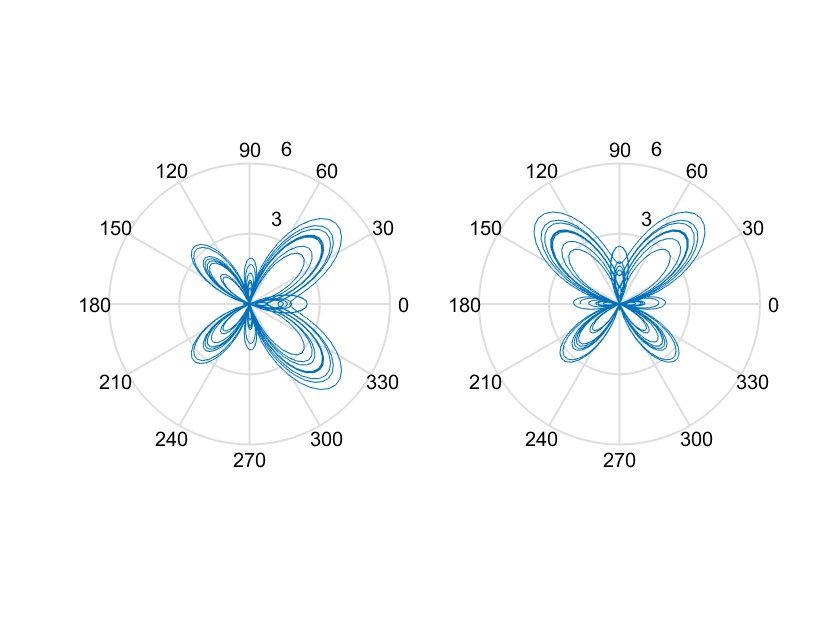
(1)绘制蝴蝶曲线。

(2)调整θ的大小可以改变曲线形状及其方向，将θ减π/2,使图形旋转90°,绘制蝴蝶曲线。