样条曲线定义和性质(二)

jucat

已于 2024-03-08 18:26:57 修改

阅读量1.2k

点赞数 13

分类专栏：算法文章标签：算法深度学习人工智能

于 2024-03-03 23:10:14 首次发布

本文链接：https://blog.csdn.net/jucat/article/details/136439039

版权

算法专栏收录该内容

20 篇文章 2 订阅

订阅专栏

参考

deboor 算法原论文，没有图解

上文

样条曲线定义和性质(一)

参数化线性插值

$y(t)=\frac{u_1-t}{u_1-u_0}P_0+\frac{t-u_0}{u_1-u_0}P_1 \\ 1 = \frac{u_1-t}{u_1-u_0} + \frac{t-u_0}{u_1-u_0} \\$

参数 u1 > u0

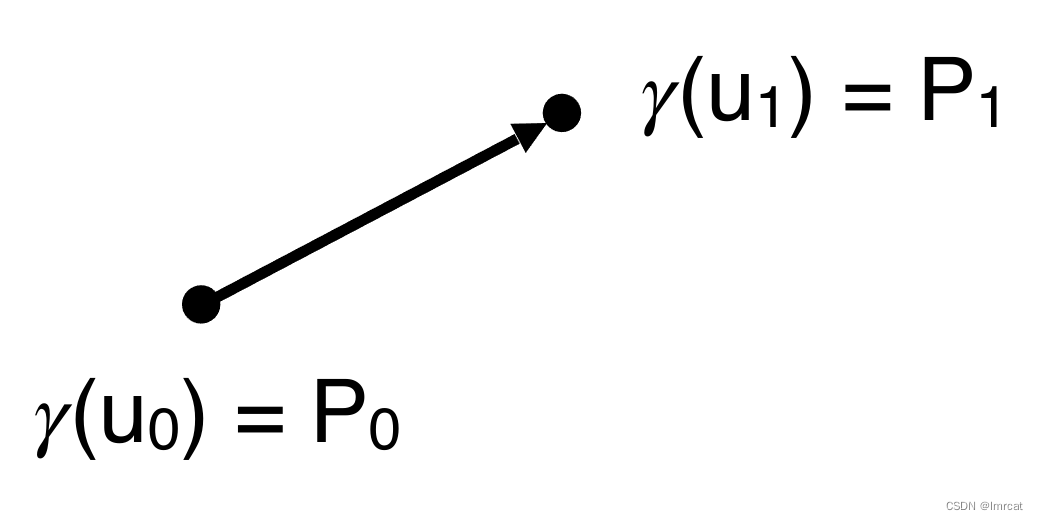
分段线性插值

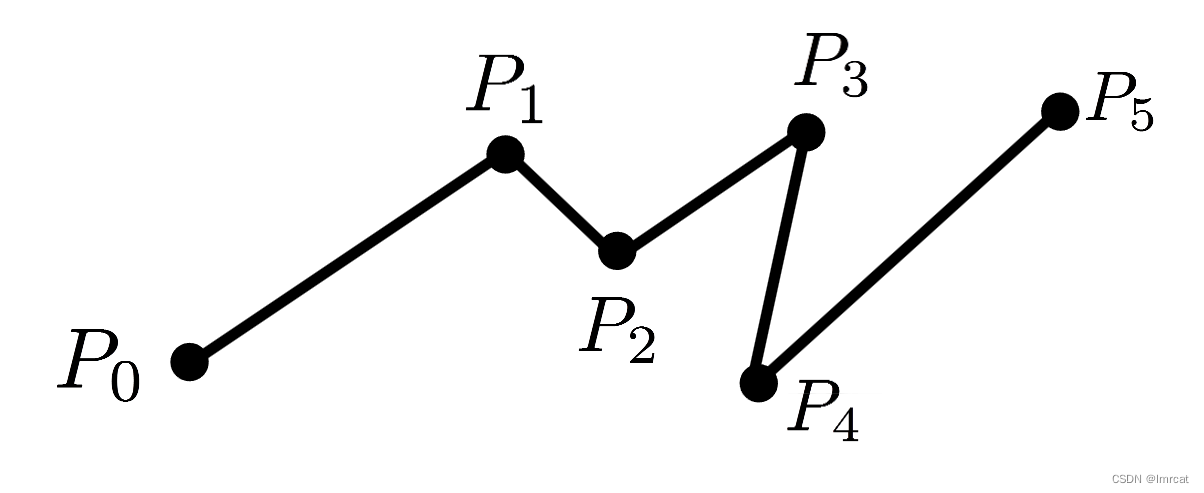
$y(t)=\frac{u_{i+1}-t}{u_{i+1}-u_i}P_i+\frac{t-u_i}{u_{i+1}-u_i}P_{i+1}$

分段参数 $u_{i+1}>u_i$ 控制了两两不同点 Px 之间的插值效果

根据公式可以知道，两点间的插值点 $P_t$ 由插值起点 $P_i$ 和插值终点 $P_{i+1}$ 以及分段参数[ $u_{i}$ , $u_{i+1}$ ]确定，参数 t 从 $u_{i}$ 移动到 $u_{i+1}$ 生成相应的插值点 $P_t$ 。

连续性

曲线函数的导数描述了曲线的连续性

$C^{-1}$ 表示线段断开连接

$C^0$ 表示线段在节点处连接

$C^1$ 表示线段在节点处一阶导数连续

$C^2$ 表示线段在节点处二阶导数连续

$C^n$ 表示线段在节点处 n 阶导数连续

de Boor 算法

B 样条曲线定义

密歇根大学对 B 样条曲线定义为控制点和基函数的线性组合：

$r(t)=\sum^{n}_{i=0}p_{i}N_{i,k}(t),\quad n\ge k-1,\quad t\in [t_{k-1},t_{n+1}] \quad (1)$

t 表示节点插值位置， $r(t)$ 是样条曲线； $p_i$ 表示第 i 个控制点；k 表示基函数阶数，n 表示有 n 个 k 阶基函数， $N_{i,k}(t)$ 表示第 i 个 k 阶基函数。

公式可以理解为 B 样条曲线由基函数对控制点的权重分配得来。

在 de Casteljau 算法中，插值权重 t 只跟当前插值点与附近控制点距离相关。

在 de Boor 算法中将插值权重交给基函数来控制。

基函数

定义

一维离散空间 $T=(t_0,t_1,...,t_m), \quad (t_i\le t_{i+1})$ ，t 称作节点(knot)，T 称为节点向量(knot vector)。一般将 $t_0$ = 0， $t_{m}$ = 1。当连续有 m 个节点相同，称该节点是重复度 m 的多重节点。节点之间的距离称为节点区间，插值权重就是由这些节点决定。

1 阶基函数

$N_{i,1}(t)= \begin{cases} 1\quad if\ t_i\le t<t_{i+1}, \\ 0\quad otherwise. \end{cases} \quad (2)$

多阶基函数

$N_{i,k}(t)=\frac{t-t_i}{t_{i+k-1}-t_i}N_{i,k-1}(t)+\frac{t_{i+k}-t}{t_{i+k}-t_{i+1}}N_{i+1,k-1}(t). \quad (3)$

基函数性质

$N_{i,k}(t)>0,\quad t_i<t<t_{i+k}$ 。
在节点区间 $t_0\le t \le t_i$ 和 $t_{i+k}\le t \le t_{n+k}$ ，基函数 $N_{i,k}(t)=0$ 。
在节点区间 [t_0, t_m]， $\sum^{n}_{i=0}N_{i,k}(t)=1$ ，k 阶基函数的和为 1。
递归性。
基函数在 $N_{i,k}(t)$ 在节点处有 $C^{k-p-1}$ 连续，p 是节点重复度。

由于相邻节点是可以相等的，当公式 (3) 中出现分母为 0 的时候，此时将该项设置为 0！

3 阶基函数例子

下面举个 3 阶基函数例子观察下基函数

定义节点向量(蓝色圆点) $T=\{t_0,t_1,...,t8\}$ ，它们落在 x 轴上(一维空间)。红色圆点 t 表示当前插值点位置。

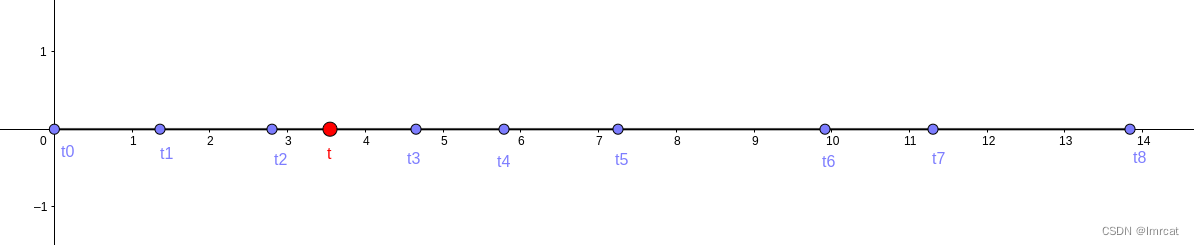
1 阶基函数

根据 1 阶基函数公式，当 t 落在节点区间 [t2, t3) 时候，有

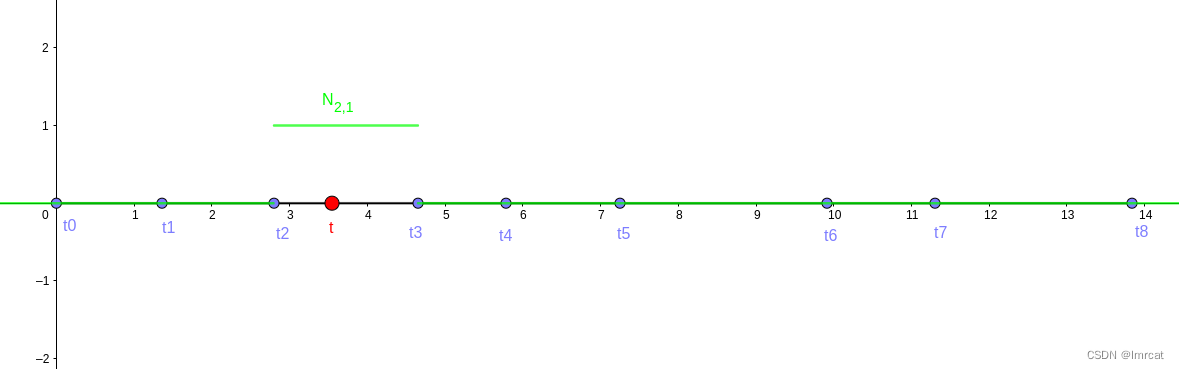
如图 fig.19 所示，第 2 个 1 阶基函数 $N_{2,1}$ 是个阶梯函数，在 [t2, t3) 区间为 1，其他区间为 0。

把所有 1 阶基函数显示出来如图 fig.20。

2 阶基函数

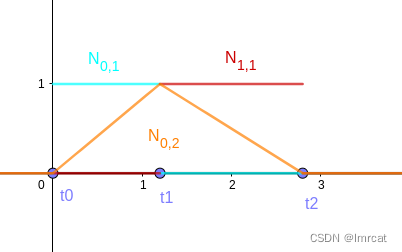
第 0 个 2 阶基函数 N_{0,2} 如图 fig.21 ，根据多阶基函数公式，由基函数 $N_{0,1}$ 和 $N_{1,1}$ 计算得来。其他所有的 2 阶基函数如图 fig.22 所示

细心的同学会发现，根据多阶基函数性质 3，对于任意插值点位置 t，都有当前 k 阶基函数和为 1 成立。可是图 fig.22 中，在区间 [t0, t1) 和 [t7, t8) ，只有 $N_{0,2}$ 的 [t0, t1) 和 $N_{6,2}$ 的 [t7, t8) 部分数据有效，该性质 3 并不成立。

其实性质 3 成立是有前提的，需要 k 阶基函数的边界是重复度为 k 的多重节点。

我们把节点 t1 拉到 t0, t7 拉到 t8

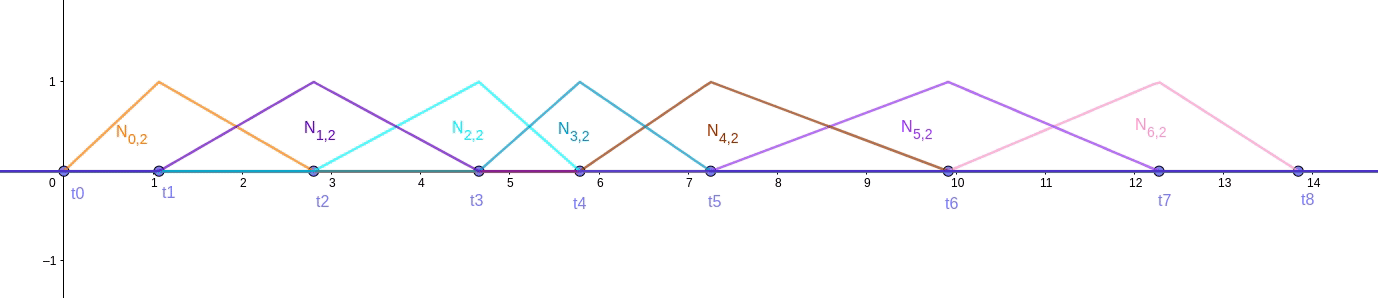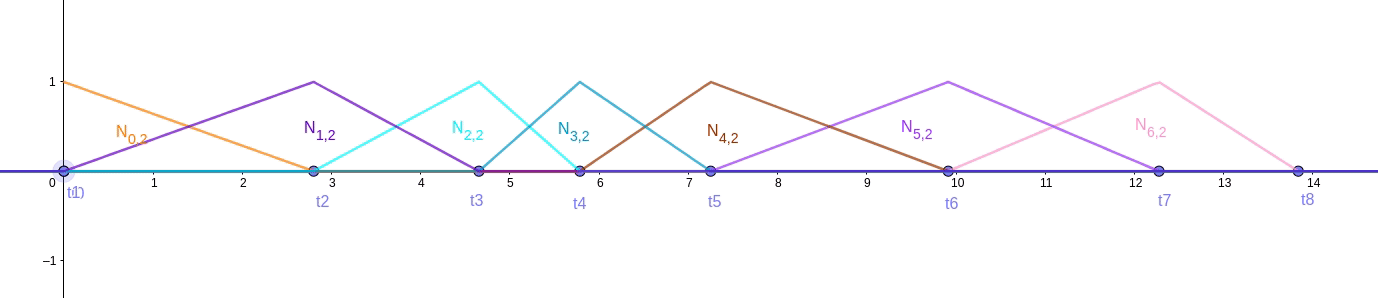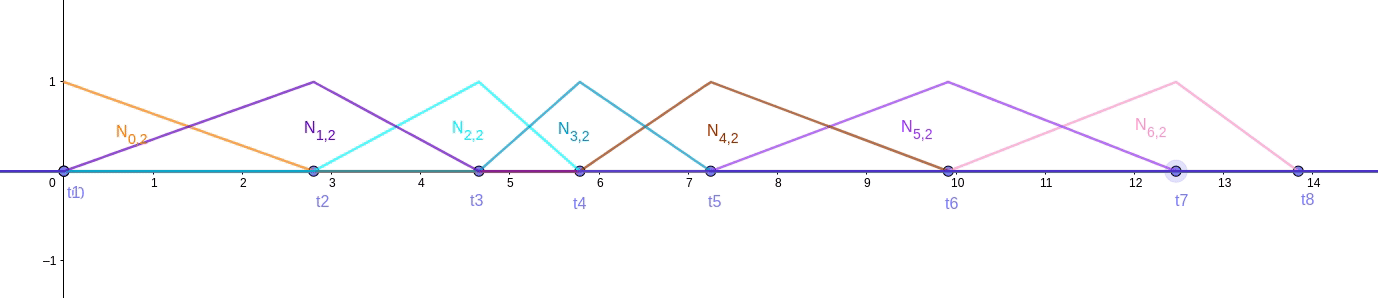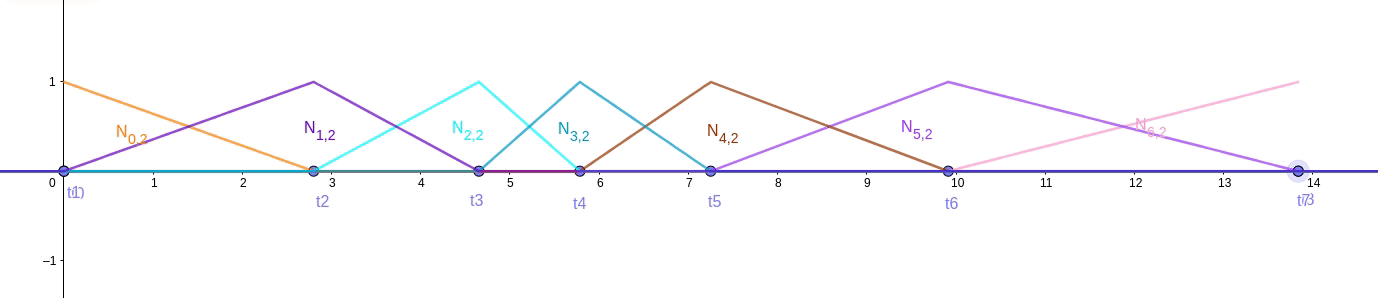
图 fig.23 中对于所有 2 阶基函数就都满足性质 3 了。

3 阶基函数

第 0 个 3 阶基函数 $N_{0,3}$ 如图 fig.24 ，根据多阶基函数公式，它由基函数 $N_{0,2}$ ， $N_{1,2}$ 计算得到。

用金字塔表示法描述这种递归计算，如图 fig.25。

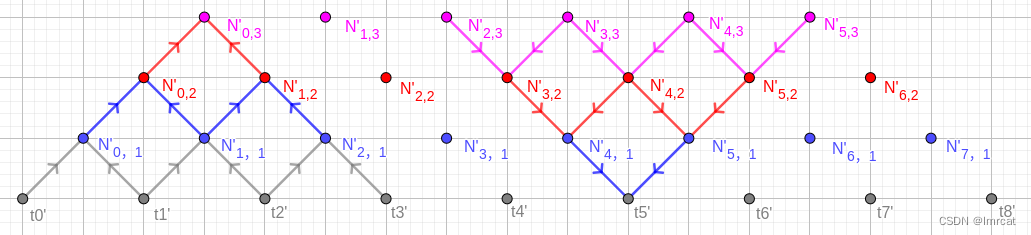
从下往上画金字塔，可以清楚地看到当前 $N_{i,k}$ 受到节点区间 $[t_i, t_{i+k})$ 的影响。

相反，从上往下画倒金字塔，可以看到节点 $t_i$ 可以影响到 k 阶基函数 $N_{i-k,k}$ 到 $N_{i,k}$ 。

其他所有的 3 阶基函数如图 fig.26 所示

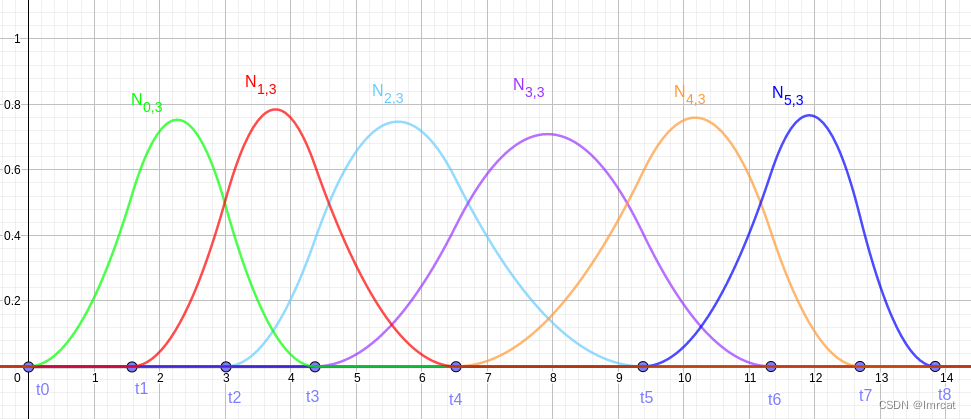
同样，为了满足性质 3，需要把边界设置为重复度是 3 的多重节点，把 t1 t2 拉到 t0 位置，把 t6 t7 拉到 t8 位置。结果如图 fig.27 所示。

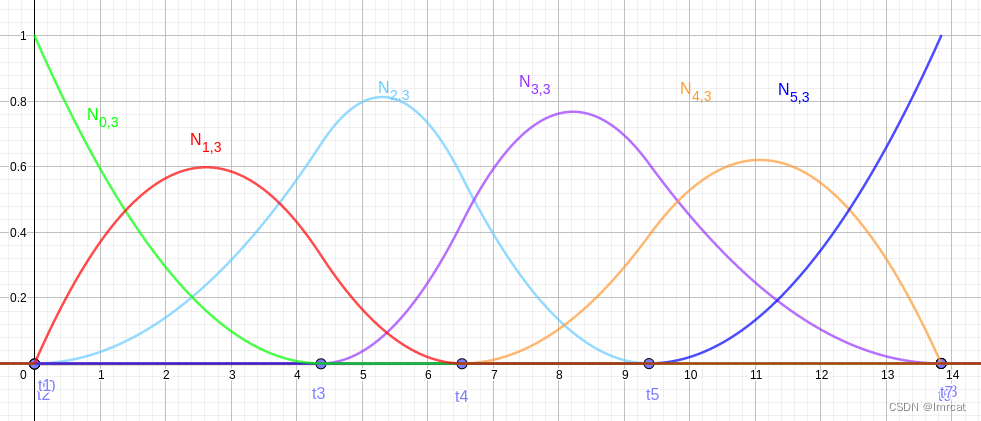
节点与控制点

b 样条曲线由控制点分权得到，权重由基函数给出。针对上面 6 个 3 阶基函数的例子，提供 6 个控制点。插值节点 t 从节点向量空间从 t0 向 t8 移动。根据公式 (3)，递归计算得到 3 阶基函数，根据公式 (1) 计算得到插值点 P。图 fig.28 显示 b 样条曲线的插值过程。

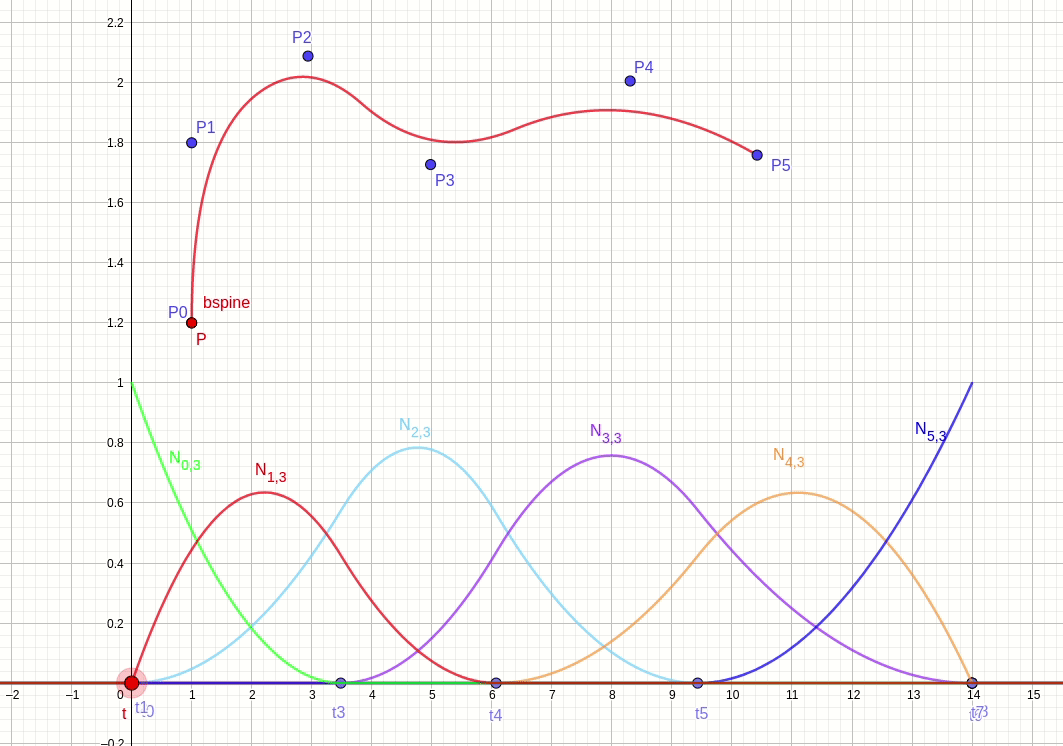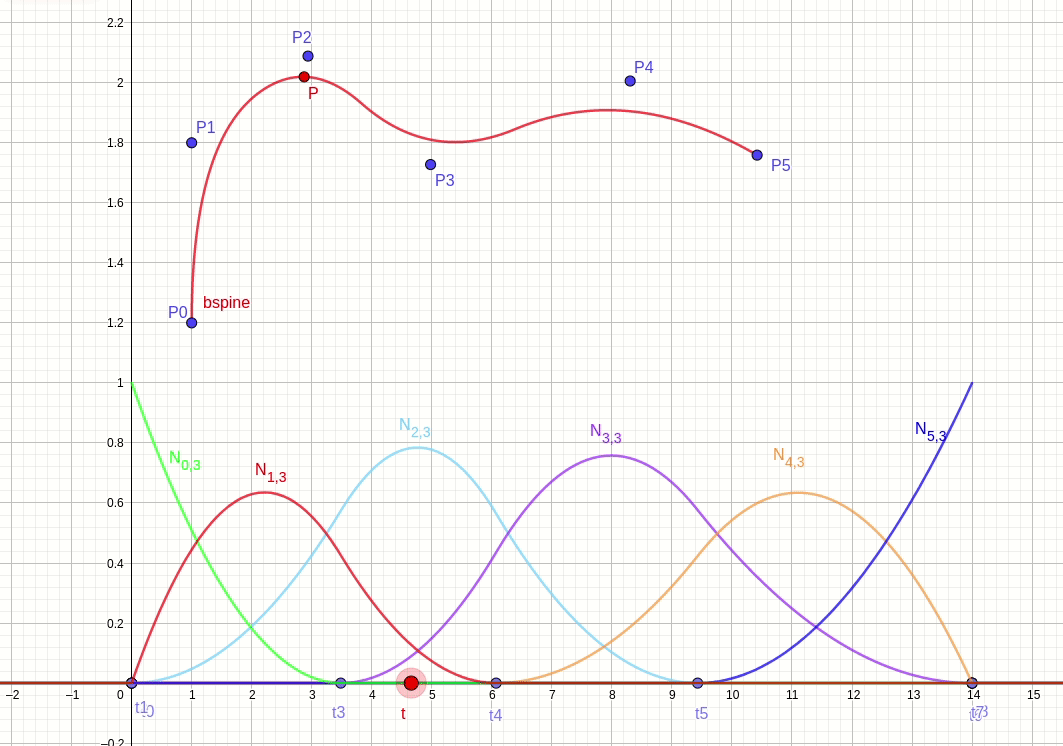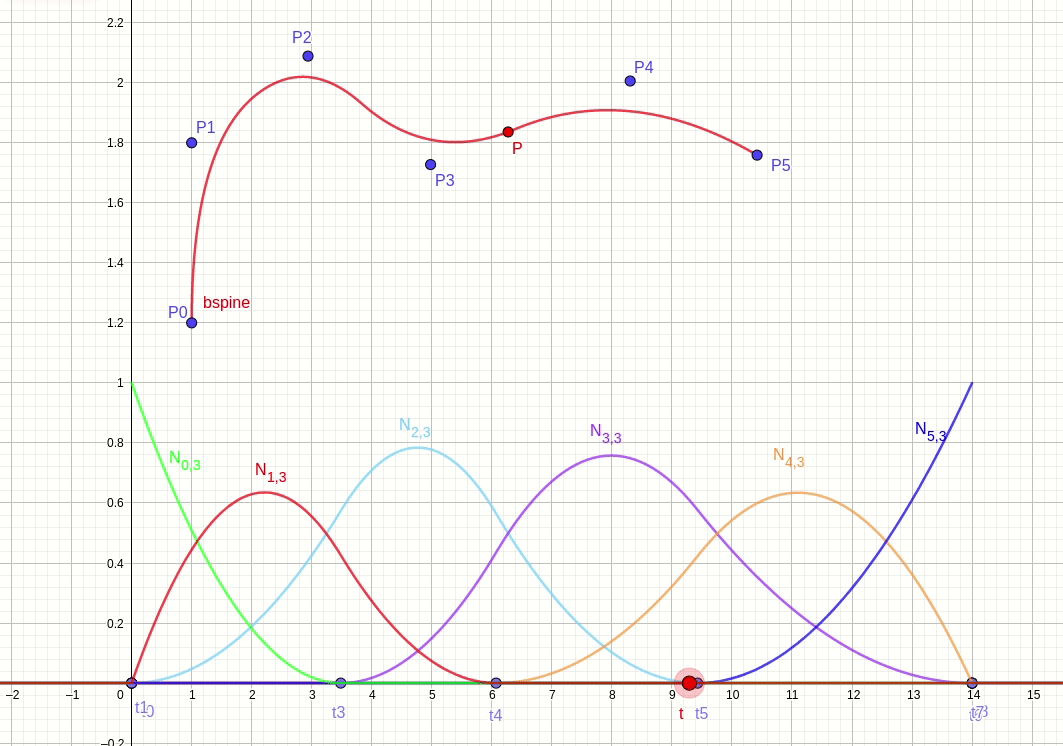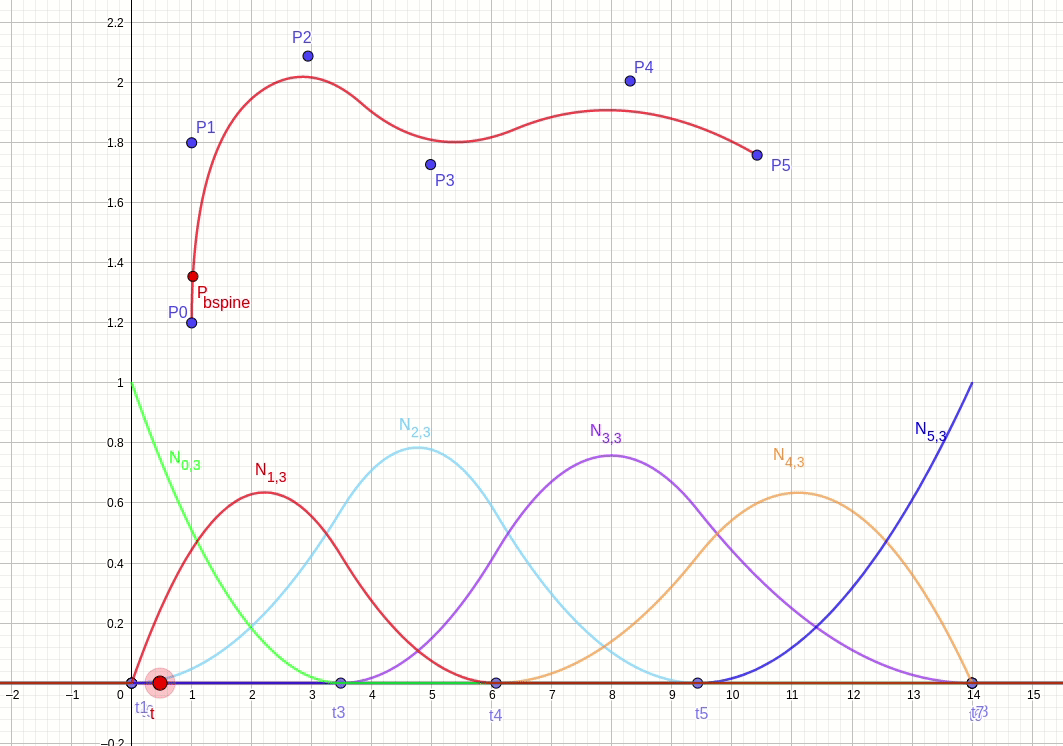
由于 deboor 算法把控制点权重与控制点分离，所以影响曲线的方法有两种，一种是移动控制点位置，一种是移动节点位置。

节点向量区间不移动（基函数不变），控制点移动的情况如图 fig.29 所示。

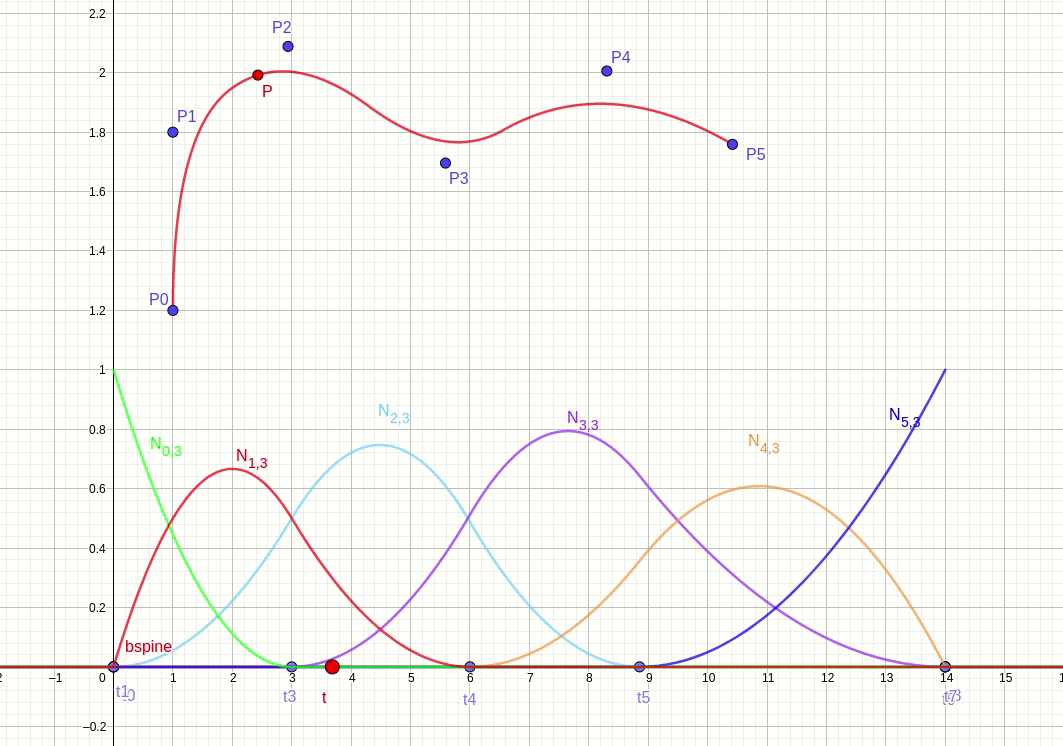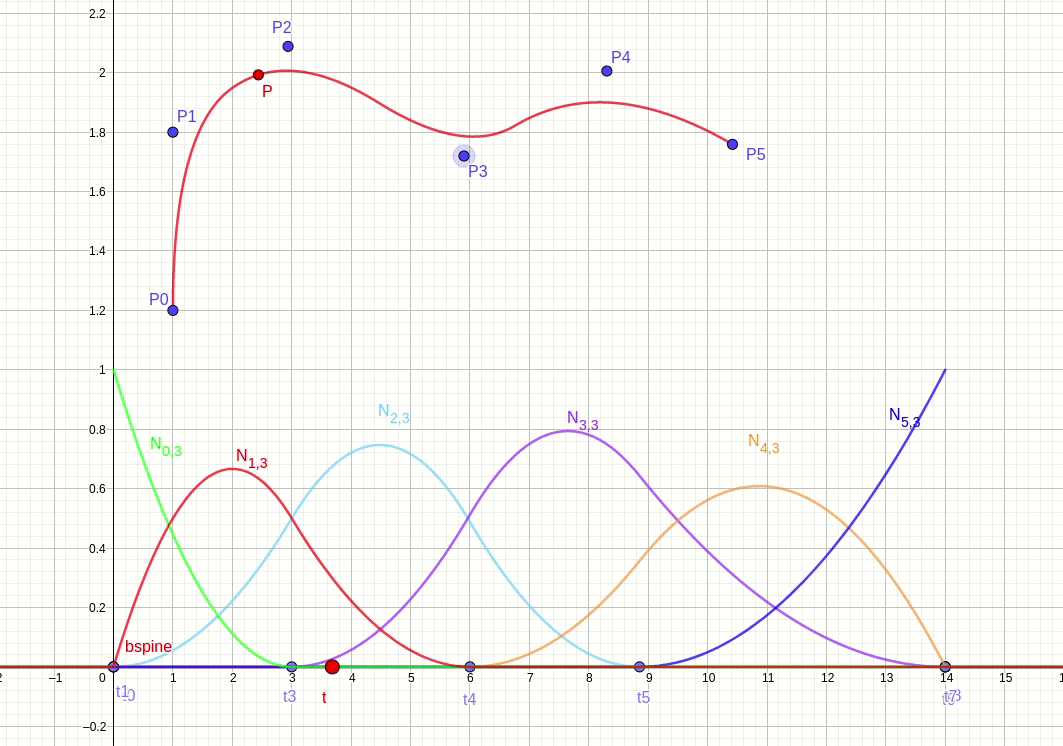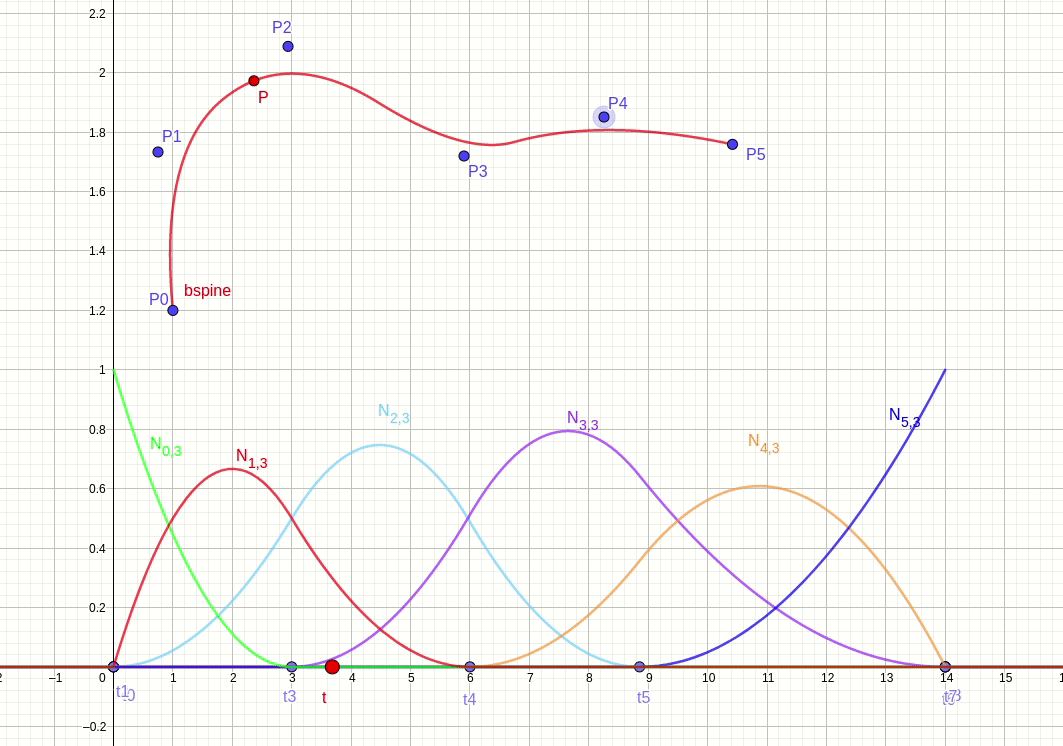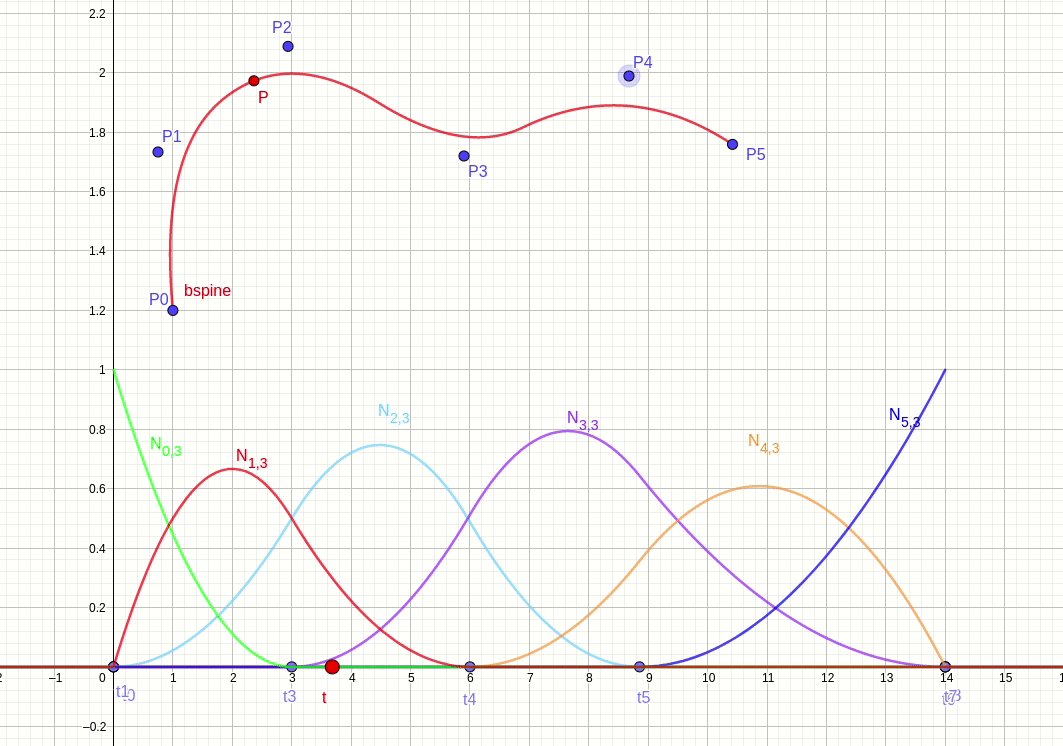
节点向量区间移动（基函数变），控制点不移动的情况如图 fig.30 所示。

将节点 t0，t1，...，t7，t8 代入公式，得到对应的插值点 T0，T1，...，T7，T8。其中 T0，T1，T2 重叠，T6，T7，T8 重叠。

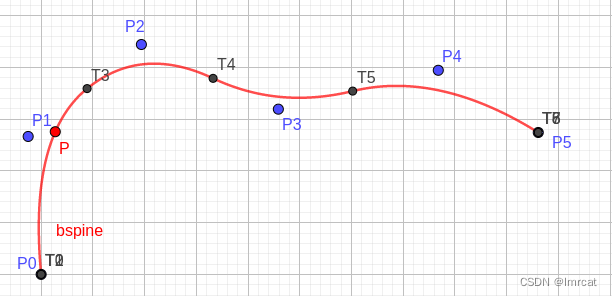
B 样条曲线性质

几何不变形：对 b 样条曲线的单位性质进行分割，保证了 b 样条曲线在平移和旋转作用下形状的不变性
结束点几何特性：
- 增加节点的多重性，会降低节点对应的插值点位置的曲线连续性。节点重复度 p(p <= k)，节点插值点的连续性为 $C^{k-p-1}$ 。当节点插值点的连续性为 $C^0$ ，意味着节点插值点与控制点重合。
  
    在图 fig.32 中，3 阶 b 样条节点 t3 其插值点 T3 位置为 $C^1$ 连续。
  
  fig.32 曲线中 t3 节点位置曲线 C1 连续
  
    在图 fig.33 中，将 t4 节点拉到 t3 位置重叠，t3 节点为重复度 p=2 的多重节点。3 阶 b 样条节点 t3 其插值点 T3 位置 $C^0$ 连续。可以明显看出曲线在 T3 前后并不平滑。
  
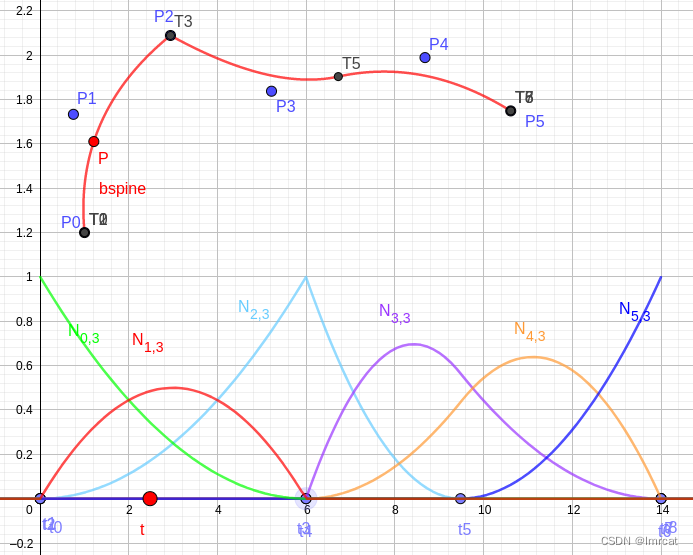
  fig.33 曲线中 t3 节点位置曲线 C0 连续
  
    在图 fig.34 中，将 t5 t4 节点拉到 t3 位置重叠，t3 节点为重复度 p=3 的多重节点。3 阶 b 样条节点 t3 其插值点 T3 位置为 $C^{-1}$ 连续。也就是说曲线在 T3 位置断开。
  
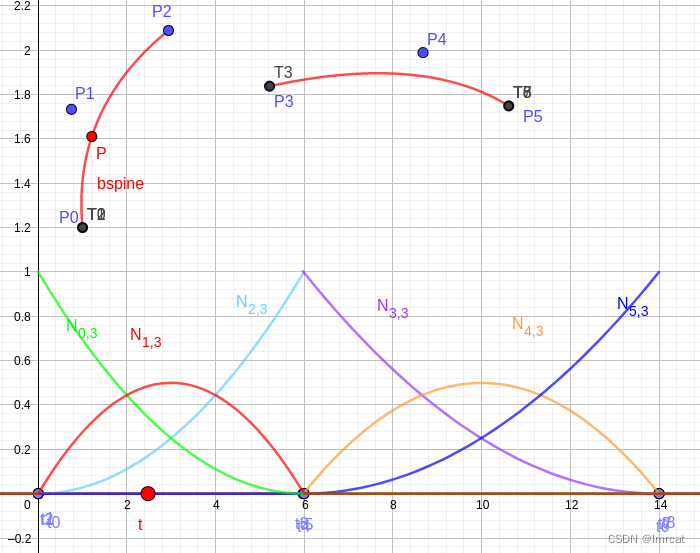
  fig.34 曲线中 t3 节点位置曲线 C-1 连续
- b 样条曲线在结束点位置与控制点相切。曲线一阶导数公式如下： $\dot{r}(t)=\sum^{n-1}_{i=0}{(k-1)(\frac{p_{i+1}-p_{i}}{t_{i+k}-t_{i+1}})N_{i,k-1}(t)} \quad (4)$
凸包性质：k 阶曲线的片段形成在其连续 k 个控制点围成的凸包中。
局部作用特性：对于 k 阶曲线，一段局部曲线(a span of curve)仅由 k 个连续控制点控制。同时，一个控制点会影响 k 段曲线。具体地说控制点 $P_i$ 能够影响节点区间 $[t_{i},t_{i+k})$ 对应的插值点，曲线 $[T_{i},T_{i+k})$ 也就是所说的“一段曲线”。

图 fig.35 显示了控制点 P3 影响曲线的局部线段 [T3，T6)。

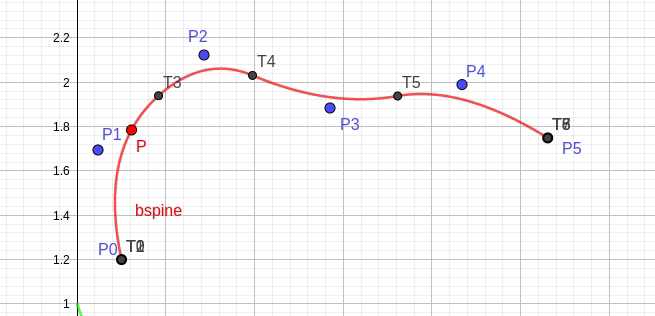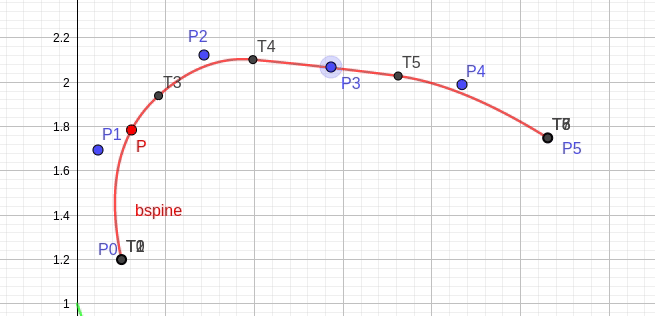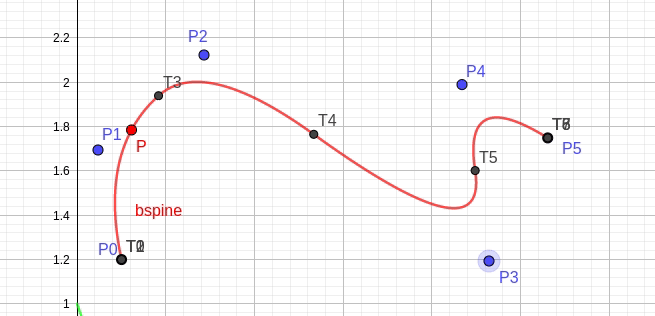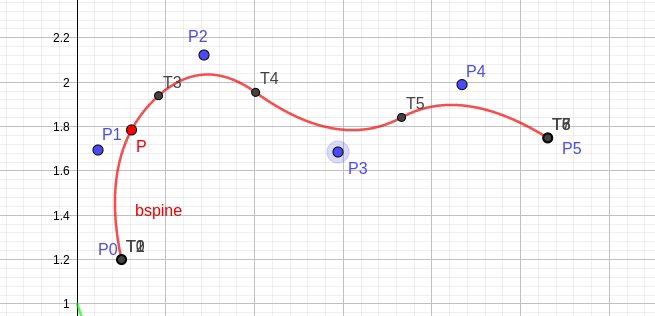
fig.35 控制点 P3 的局部作用特性
变差减少性(Variation diminishing property)：曲线与控制点形成的多边形的交点数量小于等于控制点数量。
贝塞尔是 b 样条的特例：

贝塞尔可以看做是节点向量如下的 b 样条曲线
$t=(\underbrace{t_0,t_1,...,t_{k-1}}_{k\ equal\ knots},\underbrace{t_{n+1},...,t_{n+k}}_{k\ equal\ knots}),\quad n+k+1=2k\ or \ n=k-1$