KAN与卷积网络实现图像识别的新方法

神秘泣男子

已于 2025-01-10 11:19:48 修改

阅读量1.1k

点赞数 20

分类专栏：编程探索文章标签：网络深度学习

于 2024-11-24 13:32:01 首次发布

本文链接：https://blog.csdn.net/jxjdhdnd/article/details/144006670

版权

编程探索专栏收录该内容

81 篇文章

订阅专栏

🏡作者主页：点击！

🤖编程探索专栏：点击！

⏰️创作时间：2024年11月24日10点20分

神秘男子影,
秘而不宣藏。
泣意深不见,
男子自持重,
子夜独自沉。

概述

KAN模型是一种对标多层感知机（MLP）的新型网络结构。与传统的MLP在节点（神经元）上放置固定的激活函数不同，KAN模型在权重上应用了可学习的激活函数。这些一维激活函数被参数化为样条曲线，使得网络能够以一种更灵活、更接近Kolmogorov-Arnold表示定理的方式来处理和学习输入数据的复杂关系。KAN作为一种新提出的能够替换MLP的一种神经网络基石，无论是做项目，还是发论文都是非常有吸引力的。
那么既然KAN模型是对标MLP的，那么首先来回顾一下MLP是怎么做的。

MLP回顾

MLP的本质是通过一系列的线性变换和非线性激活函数来学习数据中的复杂模式和特征。MLP可以说是神经网络领域的基石，没有MLP的发展就不会有卷积神经网络这些模型的发展。MLP本质上就是用一个线性模型再叠加一层非线性激活函数来实现非线性变换，从而达到更好的拟合函数的效果。可以用下图表示：

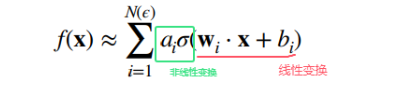
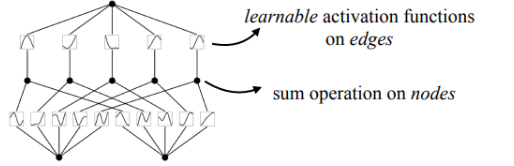
如果要用图表示的话可以用下图：

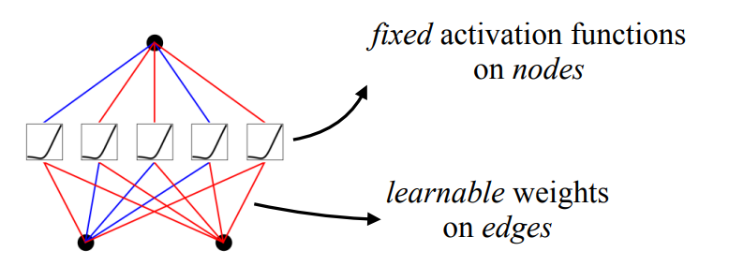
图中的线条就是MLP可学习的参数，但是激活函数都是固定的比如sigmoid、relu等。那么也可以看出来这样的MLP连接每一个节点与边就要交叉连接。如果需要做深层网络的话势必会产生大量的参数。因为每一条线都是需要学习的参数，如果再将网络扩宽的话参数会更多。最新的大模型这些都需要上千亿的参数量。

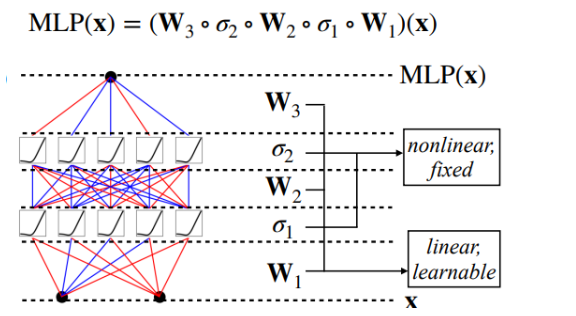
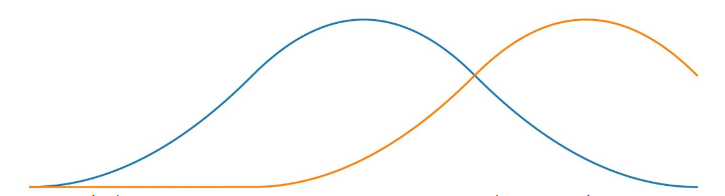
但是足够多的神经元和适当的网络结构能够逼近任何连续函数。这一理论基础称为万能逼近定理。这也是为什么要把神经网络做深做宽的原因。如下图所示：

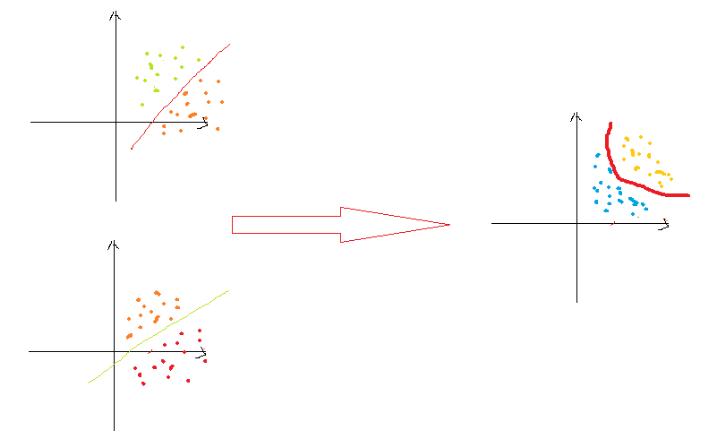
将上图两个线性函数通过一定的组合方式之后可以逼近或者形成非线性的形式。也正因为此，很多的卷积神经网络和RNN都把MLP作为基础模块。
但是，MLP也有很明显的缺点：
1.计算复杂度高：MLP的全连接层中，每个神经元与上一层的所有神经元相连，这使得参数量随着层数和神经元数量的增加呈指数增长。这不仅增加了模型的存储需求，还增加了训练时间和计算成本。
2.容易过拟合：由于参数量大且没有特定的结构约束，MLP容易在训练数据上过拟合，尤其是在训练数据量不足或噪声较多的情况下。
3.梯度消失问题：在深层的MLP中，梯度消失问题可能导致网络层数增加时难以有效训练。虽然现代优化算法和激活函数（如ReLU）在一定程度上缓解了这个问题，但对于非常深的网络，梯度消失仍然是一个挑战。
4.缺乏可解释性：MLP属于“黑箱”模型，其内部的决策过程通常不透明，难以解释模型的输出。这在需要对模型决策进行审查或解释的领域（如医疗诊断）中是一个问题。

所以KAN模型为解决这些问题提供了一定的方法，提出了一种能够替代MLP的基石。

KAN的核心原理

整体理解

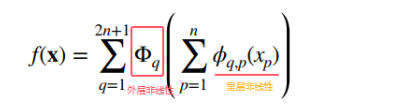
上来直接放一个公式，想必难以理解吧，但是不要慌，先注意一下上式中的2n+1后面说。里层非线性相当于是要学习的基础知识，外层非线性相当于是要学习的专业知识，有了基础才能学习专业的知识。上式中的外层函数是将里层函数的求和结果作为输入然后再求和。如果用图形表示的话就是一个两层的神经网络，但是这样的神经网络没有线性组合，而是直接的对输入进行激活。并且这些激活函数都是可学习的，不是固定的，这是和MLP的不同。

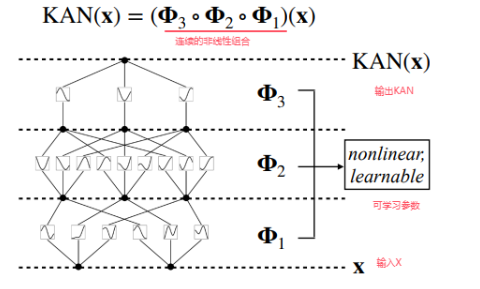
对于多层的话可以这么表示：

样条函数(Spline)

Spline提供了高平滑度的函数，因为它们是由连续的多项式段组成的，能够在节点处保持高阶导数的连续性。这种平滑性使得网络训练过程中能够更平滑地拟合数据，减少过拟合的风险。基于预定义的基函数进行计算，通常具有较低的计算复杂度。这对于加速网络训练过程和提高模型的效率是有利的。当然，目前作者选用这种激活函数也是一种尝试的选择，就像一开始的神经网络选用sigmoid函数一样。
对比MLP与KAN网络，最大的区别就是将MLP的固定激活函数+线性参数学习变为非线性激活函数的学习，其实单个的Spline函数的学习要比线性函数难，因为参数本身具有一定的复杂度，但是KAN通常比MLP的参数量更小，网络规模更小，效果相当。

整体架构

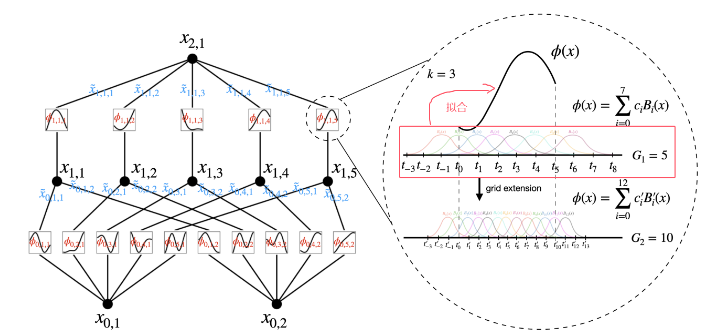
图中展示的结构中，使用了两种尺度或分辨率的组合:粗粒度和细粒度网格，在保持计算效率的同时，更加精确地捕捉和适应函数的变化。这种基础结构其实并不复杂，早期已经存在，但关键在于如何将其加深。否则，仅靠这一点内容是无法逼近复杂函数的。这正是本文的核心贡献所在。

KAN层

构建深层KAN网络时，首先需要明确KAN层的基本结构。简而言之，KAN层是一个执行一维矩阵的层，它通过一个矩阵运算将输入向量转换为输出向量。

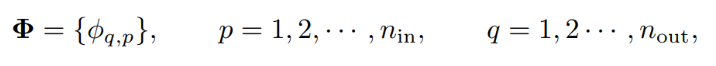
在这样一个网络结构中，假设第一层接收n个输入并输出2n+1个单元，第二层则接收这2n+1个输出作为输入，并最终产生一个单一的输出。若要实现更深的网络结构，只需简单地将多个这样的KAN层堆叠起来，这与构建多层感知机（MLP）的方式非常相似。本质上，构建深层KAN网络就是寻找并优化每一层输入输出之间的变换矩阵，即确定这些层的权重。在进行构建多层的KAN时，把KA公式中的2n+1可以进行灵活调整，这样就使得网络参数大大降低了。

KAN自动选择结构

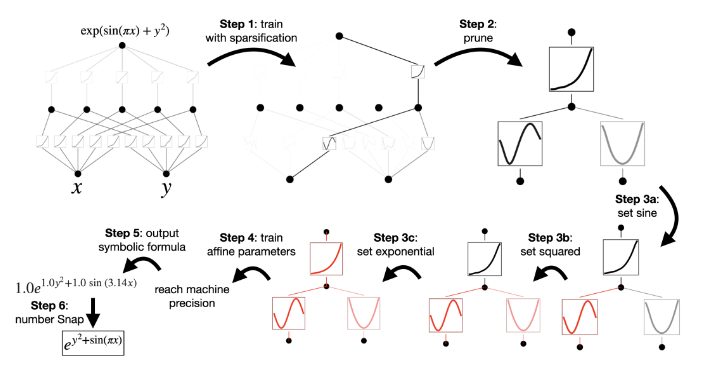
1.稀疏化处理：在利用数据集训练KAN模型的过程中，目标是让模型尽可能紧密地逼近目标函数。为了实现权重的稀疏性，类似于在多层感知机（MLP）中常用的做法，可以引入L1正则化项。L1正则化具有将不重要的权重推向零的特性，特别是那些对模型预测贡献微弱的权重。通过使权重矩阵变得“稀疏”，即减少非零权重的数量，不仅能够降低模型的复杂度，还能显著减少模型所需的存储空间和计算资源。此外，这种稀疏性还有助于提升模型的泛化能力，因为它减少了模型对训练数据中噪声的过度拟合，从而降低了过拟合的风险。
2.剪枝:在稀疏化后，进一步通过剪枝技术移除那些不重要的连接和神经元。
3.定制激活函数：这种定制化的激活函数选择可以进一步优化神经元的输出特性，使其更适合于模型的整体任务和性能要求。通过精细调整激活函数，可以进一步提升模型的表达能力和适应性。
4.优化仿射变换参数：这一步骤的目的是通过调整这些参数，使模型能够更好地捕捉数据的内在规律，从而实现对数据的最佳拟合。这里的“仿射参数”通常指的是线性变换中的权重和偏置项。
5.公式化表达：经过训练和优化之后，模型最终会输出一个简洁的符号公式。这个公式是对原始目标函数的一种近似表达，但它通常具有更高的可解释性和易理解性。

结果

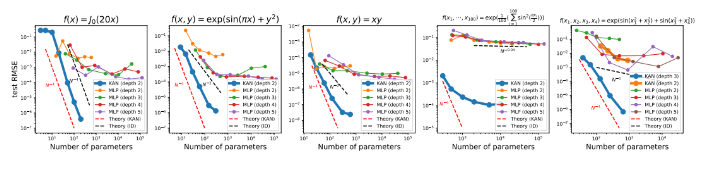
图中蓝色的线表示KAN的结果，其余是MLP的结果。横轴是参数量，纵轴是loss。参数量小，loss低。

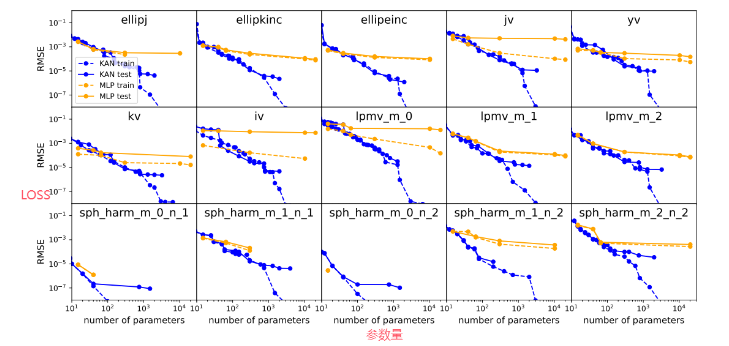
接下来简单介绍将KAN用于图像任务中的文章，并复现该论文，实现在自己数据集上的运行。

核心逻辑

KANs的核心特点在于它们的特别架构。不同于传统神经网络在节点上使用固定的激活函数，KANs在网络的连接线上使用了可调整的激活函数。简单来说，就是传统神经网络的“连接线”是固定的，而KANs的“连接线”是可以调整的。训练过程中，这些连接线不是简单的加权，而是用可以调整的“曲线”来替代。这让模型更灵活，能够更好地适应复杂的数据模式。
文中使用了与KAN网络一样的KAN层：

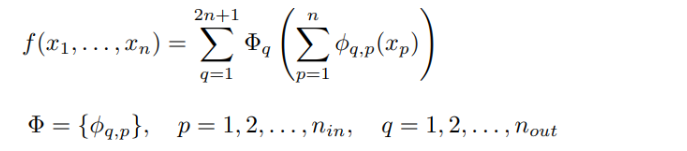
卷积Kolmogorov-Arnold网络（Convolutional KANs）与卷积神经网络（CNNs）相似，不同之处在于卷积层被KAN卷积层替代，并且在展平之后，可以选择使用KAN或MLP。卷积KANs的主要优势在于相比其他架构，它需要显著更少的参数。这得益于其网络结构的设计，因为B样条能够平滑地表示任意的激活函数，而这些激活函数在卷积层之间使用ReLU时无法找到。

通常在计算机视觉中，卷积是卷积神经网络（CNNs）中常用的一种数学操作。这个操作的基本步骤是，将一个小的过滤器（也叫核）在输入数据上滑动，并在每个位置计算点积。

而在KAN卷积中，提出了一种新的方法，和传统的CNN卷积不同。CNN中的卷积核是由固定的权重值组成的，但在KAN卷积中，每个卷积核元素是一个可以学习的非线性函数，这些函数通过B样条来表示。这种设计让KAN卷积比传统CNN卷积更加灵活，能够更好地适应复杂的数据结构。如下：

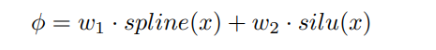
每个卷积KAN的核元素是一个用B样条表示的可学习函数ϕ，它有两个权重参数（w1和w2）和一些控制点，可以调整这些控制点来改变样条的形状。因此，每个ϕ的参数数量是“网格大小 + 2”。如果卷积核的大小是K × K，那么每个卷积KAN层的总参数数量就是K² × (网格大小 + 2)，相比之下，CNN的卷积层只需要K²个参数。

尽管卷积KANs在卷积层中有更多的参数，但由于它们使用样条函数，这让它们能够更灵活地处理空间信息，从而减少对全连接层的依赖，而全连接层通常会显著增加参数数量。这就是使用样条函数的真正优势所在：通过减少非卷积层的数量，可以减少整体的参数数量。

网络结构图

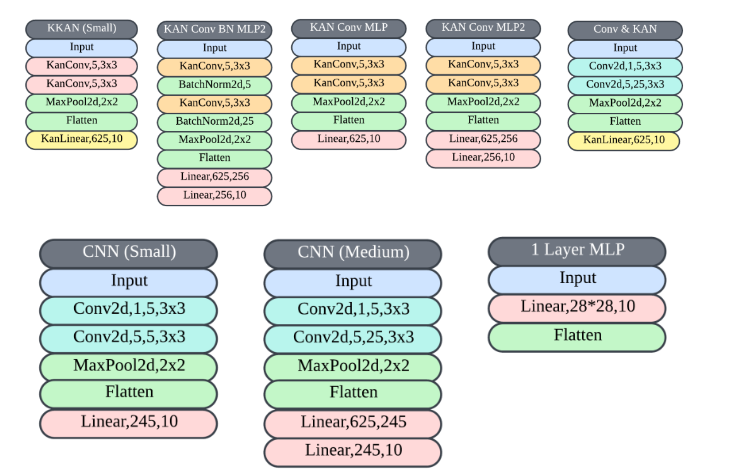
在上述结构的实验版本中，使用了torch数据集的默认划分来进行训练和测试集。此外，通过试错法选择了超参数和网络架构，但仍有空间进行深入的超参数搜索。

实验结果

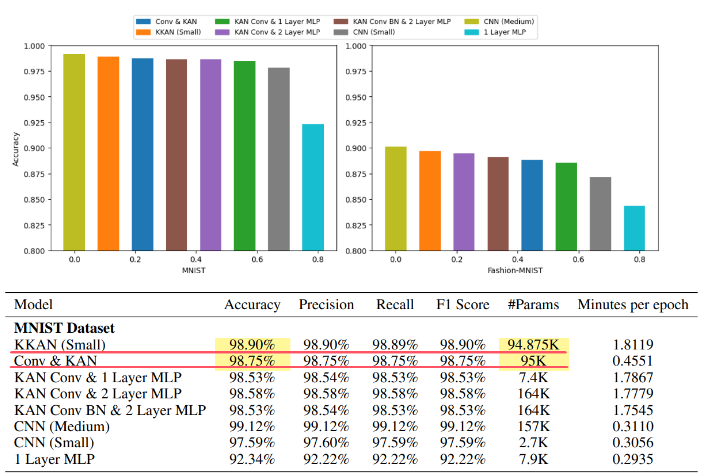
对MNIST数据集上测试的提议模型进行准确性、精确度、召回率、F1分数、参数数量和每个训练周期的训练时间的比较。与具有相同参数数量的普通卷积相比，卷积KAN的替代模型KKAN（小型）提高了0.15%的准确率。同时，具有约90k参数的KKAN的准确率比具有157k参数的CNN（中型）低0.22%。

论文复现

1.从附件下载代码

2.安装环境：

pip install -r requirements.txt
# 或者安装：
matplotlib==3.6.2
numpy==1.26.4
pandas==2.2.2
scikit-learn==1.4.2
tqdm==4.66.4
torch==2.3.0+cu118         # torch最好使用最新版。
torch==2.3.0
torchvision==0.18.0

3.按照步骤运行notebook中的每一个单元格，详见视频。

Package>>>Dataset>>>Train&Test>>>set device>>>Common Models>>>Convolutional KAN>>>Results

训练自己的数据集

1.下载数据集，数据集在附件中。脑肿瘤分类数据集。

2.构建模型：

class KANConv_MLP(nn.Module):
    def __init__(self,device: str = 'cuda'):
        super().__init__()
        self.conv1 = KAN_Convolutional_Layer(
            n_convs = 5,
            kernel_size= (3,3),
            device = device
        )

        self.conv2 = KAN_Convolutional_Layer(
            n_convs = 5,
            kernel_size = (3,3),
            device = device
        )

        self.pool1 = nn.MaxPool2d(
            kernel_size=(2, 2)
        )
        
        self.flat = nn.Flatten() 
    def forward(self, x):
        x = self.conv1(x)

        x = self.pool1(x)

        x = self.conv2(x)
        x = self.pool1(x)
        x = self.flat(x)
        x = self.linear1(x)
        x = self.linear2(x)

3.训练过程：