八、特征分析

一、特征值问题与特征方程

1.1 特征值问题

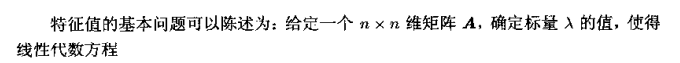
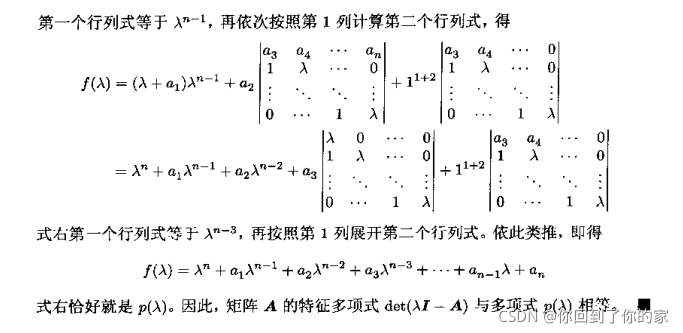
$$A\mu =\lambda \mu ,\mu \ne 0(8.1.1)$$

$$T(x)=\lambda x(8.1.2)$$

1.2 特征多项式

根据矩阵的奇异性和行列式之间的关系知，矩阵$(A-\lambda I)$是奇异矩阵，当且仅当$det(A-\lambda I)=0$，即：
$$(A-\lambda I)奇异⟺det(A-\lambda I)=0(8.1.5)$$

因此，矩阵$(A-\lambda I)$称为$A$的特征矩阵（characteristic matrix）。当$A$是$n\times n$矩阵时，展开式$(8.1.5)$的左端的行列式，即得到显式的$n$次多项式方程：

$${\alpha }_0+{\alpha }_1\lambda +\cdots +a_{n-1}{\lambda }^{n-1}+(-1{)}^n{\lambda }^n=0(8.1.6)$$

称为矩阵$A$的特征方程，多项式$det(A-\lambda I)$称为特征多项式。

为了避免矩阵$A$的特征值$\lambda$计算与特征多项式求根问题之间的混淆，常在特征多项式中用$x$代替$\lambda$。

二、特征值与特征向量

这一节重点讨论矩阵$A$的特征值与特征向量的有关计算及性质。

2.1 特征值

根据代数学基本定理知，即使矩阵$A$是实的，特征方程的根也可能是复的，而且根的多重数可以是任意的，甚至可以是n重根。这些根统称矩阵A的特征值。

关于特征值，我们需要了解如下术语：

任何一个n阶多项式p(x)都可以写成因式分解形式：

$$p(x)=a(x-x_1)(x-x_2)\dots (x-x_n)(8.2.1)$$

注意，特征多项式$p(x)$的n个根$x_1,x_2,\dots ,x_n$不一定是各不相同的，也不一定就是实的。

一般说来，矩阵$A$的特征值是各不相同的。若特征多项式存在多重根，则称矩阵$A$具有退化特征值（degenerate engenvalue）。

2.2 特征向量

若矩阵$A_{n\times n}$是一个一般的复矩阵，并且$\lambda$是其特征值，则满足：

$$(A-\lambda I)v=0或Av=\lambda v(8.2.4)$$

的向量v称为A与特征值$\lambda$对应的右特征向量，而满(足：

$${\mu }^H(A-\lambda I)=0^T或{\mu }^{H}A=\lambda {\mu }^H(8.2.5)$$

的向量$\mu$称为A与特征值$\lambda$对应的左特征向量。

这里分析下矩阵的奇异值分解与特征值分解之间的联系与区别：

2.3 与其他矩阵函数的关系

一个矩阵的特征值与矩阵的其他标量函数有着密切的关系。这里先引出特征条件数的定义。

下面讨论一个矩阵的所有特征值的集合与该矩阵的谱分析、行列式、迹之间的关系。

与矩阵的谱分析的关系

定义8.2.2 矩阵$A\in C^{m\times n}$的所有特征值$\lambda \in C$的集合称为矩阵$A$的谱，记作$\lambda (A)$。矩阵A的谱半径是非负实数，定义为：

$$\rho (A)=max|\lambda |:\lambda \in \lambda (A)(8.2.10)$$

由于$\rho (A)$是包含$A$的所有特征值在圆内或圆上的最小圆盘的半径，圆心在复平面的原点，故名谱半径。

令 λ ( A ) = { λ 1 , λ 2 , … , λ n } ， 则 \lambda(A)=\{\lambda_1,\lambda_2,\dots,\lambda_n\}，则 λ(A)={λ1​,λ2​,…,λn​}，则

$$det(A)={\lambda }_1{\lambda }_2\dots {\lambda }_n(8.2.11)$$

显然，若$A$具有零特征值，则$det(A)=0$，则矩阵$A$奇异。反之，若$A$的所有特征值都不等于零，则$det(A)\ne 0$，即矩阵$A$非奇异。

与矩阵的行列式和迹的关系

令$A$是一个$n\times n$矩阵，且$D=x{I}_n$。考虑矩阵的对角展开（diagonal expansion）$|A+D|$。以$n=3$为例，则有：

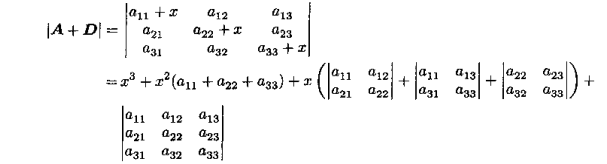
定义：

2.4 特征值和特征向量的性质

前面分析了特征值和特征向量一些典型的性质。事实上，一个$n\times n$矩阵（不一定是Hermitian矩阵）A的特征值具有广泛的性质，详见下面的汇总：

1. $n\times n$矩阵A共有n个特征值，其中，多重特征值按照其多重度计数。
2. 若A是实对称矩阵或Hermitian矩阵，则其所有特征值都是实数
3. 关于对角矩阵与三角矩阵的特征值：
   若$A=diag(a_{11},a_{22},\dots ,a_{nn})$，则其特征值为$a_{11},a_{22},\dots ,a_{nn}$
   若$A$为三角矩阵，则其对角元素是所有的特征值
4. 对一个$n\times n$矩阵$A$：
   若$\lambda$是$A$的特征值，即$\lambda$也是$A^T$的特征值
   若$\lambda$是$A$的特征值，则${\lambda }^{\ast }$是$A^H$的特征值
   若$\lambda$是$A$的特征值，则$\lambda +{\sigma }^2$是$A+{\sigma }^{2}I$的特征值
   若$\lambda$是矩阵$A$的特征值，则$\frac{1}{\lambda }$是逆矩阵$A^{-1}$的特征值
5. 幂等函数$A^2=A$的所有特征值取0或者1
6. 若A是实正交矩阵，则其所有特征值为1或者-1
7. 特征值与矩阵奇异性的关系：
   若A奇异，则它至少有一个特征值为0
   若A非奇异，则它所有的特征值为0
   
   
   
   
   
   矩阵A的奇异值问题往往转化为相应矩阵的特征值问题求解。实现这一转化有两种主要方法：

2.5 矩阵的可对角化定理