第四章 Global and Detailed Placement [VLSL Physical Design 学习笔记 ]

4.1 简介

在将电路划分为更小的模块并对布局进行布局以确定块轮廓和引脚位置之后，摆放(Placement)寻求确定每个块内的标准单元或逻辑元件的位置，同时实现优化目标，例如最小化元件之间的连接的总长度。

是的，这一章节也和模块的位置的确定有关，区别在哪里呢?我大概总结了一下:
第三章是一个比较粗的粒度，不要求具体到把一个个原件放到芯片上的单元格上，只是把大概确定长宽的模块放在全图，而第四章所描述的"Placement"粒度更细，会把电子元件与芯片上的单元格对应。

以下给出第三章和第四章的优化目标的对比:
第三章:
1,总面积 2,估计的总布线长度 3,信号延迟
第四章:
1,估计的总布线长度 2,加权的总布线长度 3,最大切割度(Maximum cut size) 4,布线拥挤程度
总的来看第三章第四章内容相似,但是第三章主要篇幅在讲模块的放置和如何优化总面积，第四章重心多在减少布线长度，与合法化(将电子元件放在芯片单元格)。

具体而言，全局放置（Global Placement第4.3节）会把可移动的单元给一个大致的位置，而详细放置（Detailed Placement ,第4.4节）则将对象位置细化为合法单元位置，并强制执行不重叠约束。详细放置会在全局放置基础上进一步优化线长，电路延迟等优化目标。

4.2 优化目标

大致是以下四个目标:
1,减短线长
2,减少格子边切割的线数
3减少布线拥挤
4减少信号延时

下面是详细一些的四个优化目标的解释:

摆放的线长(Total wirelength with net weights (weighted wirelength))

说到摆放的线长，以下给出“线长”的表示方法(Wirelength estimation for a given placement):

对于“线长”的定义，我们需要定义多引脚线和双引脚线的线长。对于双引脚线，这里不采用欧式距离，而是采用上面的公式进行定义。
而对于多引脚线，以下给出了几种定义方法:
1,半周长线长(half-perimeter wirelength,HPWL)

如图是连接四个点的网络。这种方法找到最小的容纳这些点的矩形，取一半这个矩形的周长作为网络线长。
这种方法较为准确，随着点数的增长，线长估计值大约与$\sqrt{p}$成正比
2,完全图模型(complete graph (clique) model)

这种估计方法假设点之间有两两相连的连线。不难得知连线数为:

这里算法又假设把这些点连起来，在实际操作中只需要一个生成树，这个生成树有p-1条边，那么，结合上式，冗余的计算大约是$\frac{p}{2}$倍,故估计的时候再除以这个数，作为修正。

其他等等书上还列了六种表示方法，并给出了一些分析，这里简单列举三个一笔带过，总之是各有优劣。
链式表示就是以x或y坐标排序，依次连接。会过度估计线长，拓扑结构容易随着摆放改变而改变
星式表示就是找个原点，依次连接剩余点，会过度估计线长，表示多引脚线较方便
方形最小生成树(rectilinear minimum spanning tree,RSMT)就是做一个最小生成树，然后算树的边长和

最后，把各网络线长加权平均即可得到第一个优化目标函数

以下是一个带有部分线的一个摆放的例子，要求用最小生成数法评估其线长。

最大切割量(maximum cut size)

此处与最大割区分不叫最大割，此处最大切割量意思是，若有一些能把布局一分为而的划分线，这些划分线会与导线相交并有各自与导线相交的数目，其中最大的数目就是最大切割量。
对于是否相交的定义如下例所示:对于一个网络来说，若存在两个引脚，其中一个引脚在L侧，另一个在R侧，我们就说它是与这条竖直切割线是相交的。

以下是严格定义:
定义$V_p$和$H_p$分别是$P$的全局垂直和水平剖切线的集合。
定义$\Psi (cut)$是与切割线$cut$相交的网络的集合。
定义${\psi }_P(v)=|\Psi (cut)|$，是$\Psi (cut)$这个集合中包含的网络的数目。
则$X(P)$定义为所有垂直剖切线$v\in V_p$的切割数${\psi }_P(v)$的最大值。
$Y(P)$定义为所有垂直剖切线$h\in H_p$的切割数${\psi }_P(h)$的最大值。
$X(P)$ 和$Y(P)$代表着这个芯片上横纵方向的格子边上需要的最少的布线资源。
举个例子，$X(P)=10$的时候，有些纵边会需要有10条导线穿过，所以起码这条纵边上要有10个布线轨道。水平方向的$Y(P)$同理。
所以可以得出结论：$X(P)$和$Y(P)$在资源允许的范围内，是可布线的必要不充分条件。
通过优化$X(P)$和$Y(P)$,我们能减小布线压力最大的边所切割的导线数,从而提高可布线性。

若$L(P)$看作是所有水平和竖直边界线的切割导线数之和，

那么我们也可以把它理解为所有导线跨单元的次数，通过减小这个值我们可以优化线长。

以下是一个例子,这个例子中，若使用RMST模型进行布线，总的$L(P)=8$,$X(P)=2$,$Y(P)=3$。而且把b模块往上挪一格能进一步减小局部的拥挤度，$Y(P)$会降到2，$L(P)$会降到6。

布线拥挤程度

若从密度的角度来看拥挤程度,拥挤程度可以看作是资源的占用比。
举个例子，下图是一个switchbox和一个channel,switchbox有横、纵布线轨道，而channel只有横向布线轨道。

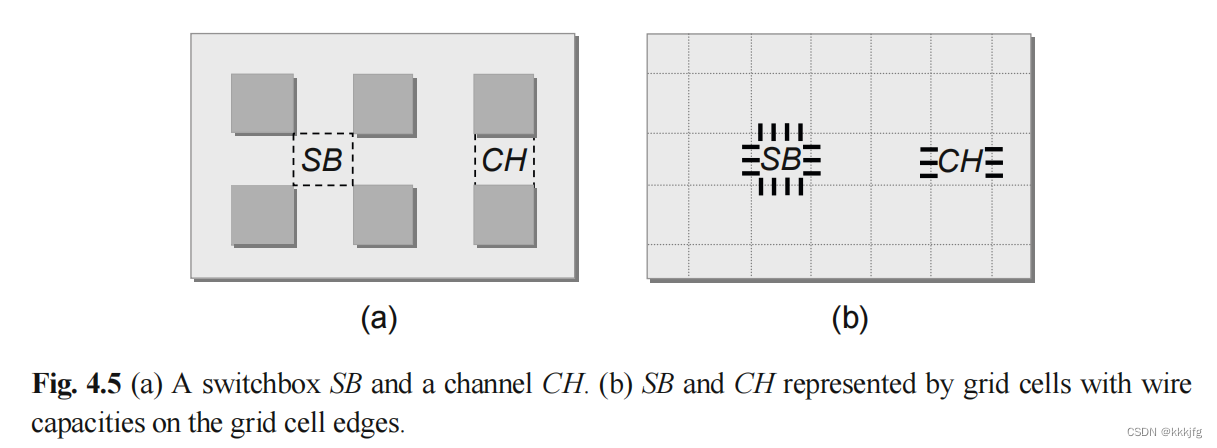
在门级别的设计里，这些模块都是固定的，布线轨道无法改变。所以为了成功布线，我们必须保证设计出来的布局经过每个switchbox或者channel的线数都在其轨道数范围之内。

设一个布局为$P$，在这个布局中两个相邻单元的交边为$e$,则这两个单元之间拥挤程度就是${\phi }_P(e)$,${\eta }_P(e)$是穿过这条边的连线数，${\sigma }_P(e)$这条边上的可布线轨道数。

对于一个布局$P$来说，它的布线拥挤程度(wiredensity)就是它里面所有边的拥挤程度的最大值。
易知，当$\Phi (P)⩽1$时，这个布局是可布线的，当$\Phi (P)>1$时，有些线需要改道绕行穿过一些不那么拥挤的边，以缓解拥挤程度。
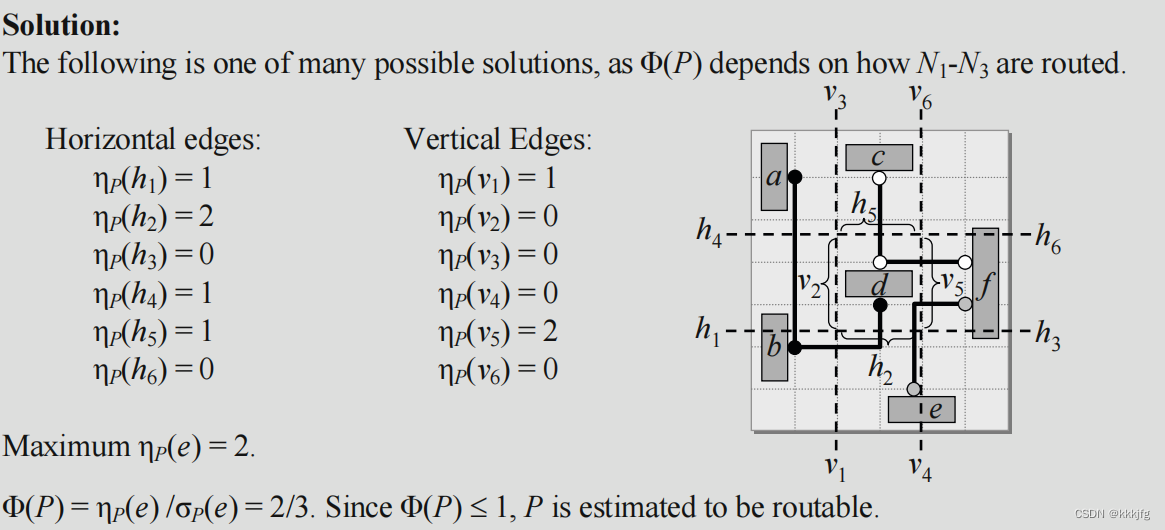
如下所示是一个例子，所有边的轨道数都是3，我们需要用RMST模型进行布线，并评估是否是可布线的。

RMST生成的布线结果如下，经计算，$\Phi (P)<1$,该布局是可布线的。

信号延迟
在现代工艺下，影响时钟频率的延时不再是门延时，而是信号在线路上传播的延时。
延时一般用静态时序分析(static timing analysis)进行优化和验证。延时一般有两个常见的术语，一个是实际到达时间(actual arrival time, AAT)，一个是必要到达时间(required arrival time, RAT)。实际到达时间是指从时钟周期开始，到信号传递至某个单元的测得的实际用时，必要到达时间指的是在一个时钟周期内，电子元件正常运作所需的时间。在各种限制之下，若芯片要正常运转，$AAT(v)\le RAT(v)$

4.3 整体放置(Global Placement)

本章包含分属于三类的四个整体布局算法。
1，基于分割的算法(partitioning-based algorithms):这类算法通过不断把图细分为子图，把总网络划分成子网络，直到这些布局小可以到我们可以直接得出其最佳布局，则停止不再细分。本节将介绍这类方法中的基于最小割的放置(min-cut placement).
2，基于解析式方法的放置(Analytic techniques):这类方法通过对目标进行建模，并构建目标函数(损失函数)，并对这些函数(可以是二次的或者非凸的)进行优化。本节将介绍这类方法中的两个算法，二次布局(quadratic placement)和力导向放置( force-directed placement)。
3，随机算法，这类算法通过随机移动模块来优化损失函数。本节将介绍这类方法中的模拟退火算法。

以上是这四种方法的示意图。

4.3.1基于最小割的放置(Min-Cut Placement)

最小割布局算法最早于1970由M. A. Breuer提出，它用分割算法不断地将现有布局和网络进行划分，直到最终每块都小的能直接得出最优方案。
切割一般基于启发式算法来减小每次的割大小，如使用2.4提到过的Kernighan-Lin(KL)算法和 Fiduccia-Mattheyses(FM)算法。
算法流程的伪码如下。

理论上算法最好同时优化$X(P)$,$Y(P)$和$L(P)$,但这在计算上行不通，且就算每一步都是最优的，组合出的最终结果也未必最优。所以以下介绍的是一种较为简单的办法，就是迭代式地一次只关注一条割线进行优化。比如可以第一次横割，第二次纵割，逐渐进行切分。

如图就是两种逐渐切割地方案，途中阿拉伯数字1234代表切的顺序。图a先是横着切一下，再纵向用2a，2b分别割开两个子块，3，4步同理，b则是另一种，先横着分到分无可分了(比如已经切到标准单元的大小了)再考虑纵向的切割。
如下图是例子，都是两个交替方向进行切割的，分割算法分别应用了KL算法和FM算法。
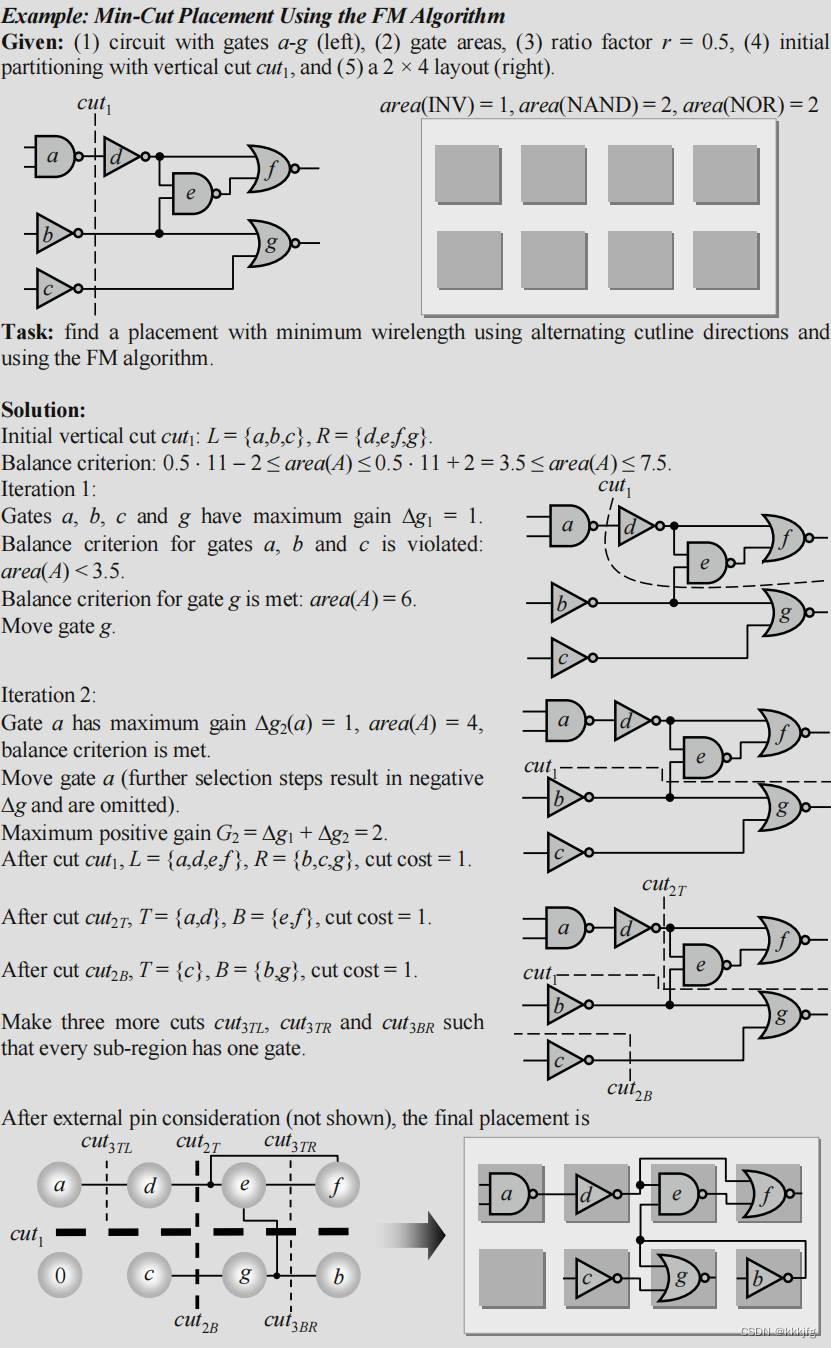
看完上面的例子，可能很多人都有了一个疑问:把一个模块分成两半之后，两个空格和两个子模块之间怎么找到对应关系呢?是可以随便填吗?
在简易版的算法中是无所谓的，但如果要考虑外部线，就要进行改进。

如图，在这个布局中a有一个外部连线，与边界交于$p^{\prime }$，这时a应该尽量与$p^{\prime }$接近，比如要是把这个模块分成两半，a放在左半，则a与$p^{\prime }$之间的连线就要长一些。
A. E. Dunlop 和 B. W. Kernighan发明了"终端传播算法(terminal propagation)"，就是在进行分割的时候若虚拟节点(类似上图中的$p^{\prime }$这种交点)与分割线比较近，则不考虑，若距离较远，则看作一个位置固定的节点加入计算。
具体来说，算法执行的时候会把一个切割块之内的所有节点都视作放在块正中间，而“近”的区域定义为整个区域的中间1/3的这块条状区域。下面是一个例子:


如上图中，第一次划分只把ab划到左边，cd划到右边，那么这时我们下一次划分ab所在模块为上下两部分时，由于ab与cd都挤成一团位于各自模块的中间，连线与应划分的横线重合，在中间三分之一的位置，所以划分a与b的时候不做考虑，直接分就行了。但a与b分完之后b，d连线就上浮到了距离顶部1/4的位置，显然不在中间1/3里，所以划分c与d的时候就把交点也看做一个虚拟点来计算割。这样d就被留在了上面。
在处理多引脚连线的时候同理，根据引脚位置判断是否忽略该节点即可。

4.3.2 基于解析式方法的放置(Analytic Placement)

这类方法通过建模整放置的目标函数或者损失函数，然后这些目标和函数使用一些数学手段，比如数值分析和线性规划，进行优化。通常来说，这类建模会把一些模块视作一些无穷小的点，然后构造一个可导的损失函数进行优化。比如在优化线长的时候，可以计算二次距离而不是直线距离来方便求导。不过这类方法有时候会让两个模块过于近而产生重叠，因而需要一些后处理操作进行分离和去除重叠。

基于二次函数优化的放置(Quadratic placement)

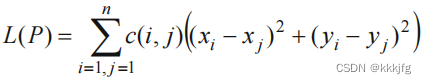
这个方法使用二次欧氏距离作为线长的损失函数。$x_i,y_i$和$x_j,y_j$表示点的中心坐标。总的损失就是各模块的中心距离平方的加权和。
使用二次距离作为损失函数会惩罚和约束过长的模块距离。
这个方法一般分两步，在整体放置步骤中有时会形成一些集群(clusters)从而会有一些重叠，这些集群在后续的详细放置步骤中会被拆开来再放，以去除重叠产生合法的摆放。

如何求解呢？由于这里举例的这个方法比较简单，就是距离平方的加权和，所以求解方式也比较简单。
首先，这个损失函数或者说目标函数，可以拆解成x方向和y方向的。

然后求导求极值点即可。

x,y方向的解求解上面两个方程即可。(以上若i不等于j，则$A[i][j]=-c(i,j)$,i=j则$A[i][j]$等于第i个单元的所有连线权重和)
以下是一个用这个方法进行放置的例子。

力导向的放置(Force-directed placement)

这个方法中，整个布局被建模成了一个"质点-弹簧(mass-spring)"系统，每个单元模块是一个质点，每条连线视作一根弹簧，对连接的两个模块有引力作用。那么，若这个布局中模块是可移动的，在若干次迭代后会达到平衡态。相比于初态，平衡态的线长是更优更短的。

在这个系统中，弹簧弹力正比于模块间的距离，弹簧势能正比于距离的平方。

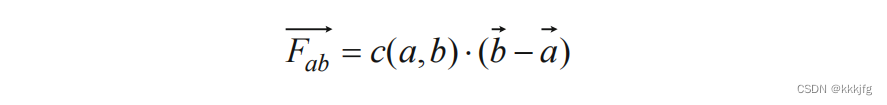
由于弹簧对一个单元i的力是势能对位置的偏导数，所以最小化欧氏距离的过程是最小化势能的过程也就是最小化线长的过程。从这个角度看，力导向的放置算是基于二次函数优化的放置的一种特例。

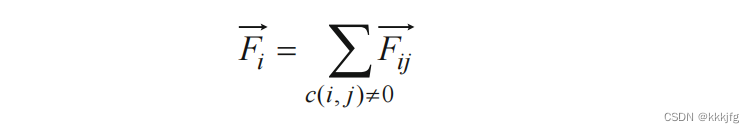
这个算法的求解方式是求解受力方程使受力等于0

一个可能的扩展是，可以不仅计算引力，也把不相连单元之间的斥力纳入考虑，以防止重叠。

求解方式可以是计算每个单元的平衡点，并放置到平衡点上，反复此过程并逐步改善。
首先列出受力方程:

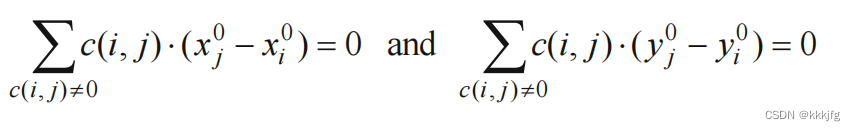
平衡点是:

这个解看上去就是待计算单元的连接单元的位置加权平均。
由于算平衡力的时候的几何关系已经变了，所以挪完之后可能依然不是平衡的，这时候就要多次迭代直到找到解。
以下是一个例子。


这个例子很简单，就a能动，直接代入公式，用$In1In3,Out$的位置加权平均即可。

对于较复杂版本的算法来说，除了要考虑平衡点，还需要考虑平衡点被其他单元占用的情况。
以上第5行是一个循环，会反复选择模块求其平衡点，在在全部单元都移动过之后结束，或者达到终止条件之后停止。感觉第五行怪怪的，是不是while(!(ALL_MOVED(V)||STOP()))比较正常?
算法每次回寻找没有移动过的点里面连接线最多的(第6行)，即优先解决线多的点的平衡问题。
然后是分类讨论，若这个点没有被占用(第8行),则直接把这个模块挪过去(第9行),若被占用，则再使用别的算法重新考虑(第11行)
以下是平衡点被占用的情况下寻找合法点的方法:
假设p是待安置模块，q是占用了p的平衡点的模块

• 如果可能，则直接放在被占用点的附近的位置
• 计算p和q交换的收益，如果交换之后线长减小，则直接交换
• 链式移动，先把p放在平衡点上，然后再把q放在下一个位置(书上原话next postion，不清楚这里next是怎么算的，不知道是不是就是放附近)上，若q的新位置被占，也是相同方式处理，即抢占平衡位置，再考虑被抢占位置的模块
• 涟漪移动(ripple move), 先把p放在平衡点上，然后再转而考虑q的新的力平衡位置。
  
  如上是一个既不考虑链式移动，也不考虑涟漪移动的，如果平衡位置被占，只考虑了交换。如上这里本来打算把$b_3$换到位置0上，发现没增益就不换了，然后考虑$b_2$，平衡点在位置2，也就是$b_3$所在位置，交换后发现有得赚，就换了。换完刚好达到了最优态。

考虑涟漪移动的力导向放置

在力导向的放置里，如果力平衡点是空的，肯定直接就放过去了(11-16,28-32,可以看到这两类放完直接就end_ripple_move=true了，直接考虑下一个点就行了)。那如果被占领了呢?
考虑涟漪移动的力导向放置实际上可以进行包含两类的分类讨论:
1,若被占领的位置的点只是随便放那的，没有经过精心计算，那么我们则大致推测，可以占领。就占了再说(34-40)，这个被抢占位置的点再去算平衡位置，当然，被抢占再考虑这可能是一个循环过程，不一定一下就能找到(第8行)。
2,如果之前那个点是先前就考虑过，由于点大致是按照连线多先考虑来排序的，我们就假定抢占不会赚，就放在平衡点附近好了(18-26)

由于怕所有点只挪一次并不能达到最优态，我们需要有一个时机去解放各点，进一步优化。解放太早呢，可能会造成能动的点太多，互相抢占的问题，太晚，则流动性不强。这里用了一个abort_limit来控制。当出现上面讨论中的第二种，平衡点撞到是已经考虑过了的点，就abort_count加一，当且仅当加到abort_count=abort_limit的时候，解放点允许他们继续移动。

这里这个算法在循环布局中各个模块，与尝试进行挪动(8-41)之间，还加了一层循环，即第4行，对每个点都试探若干遍才罢休，怕由于有的模块锁住了一次循环到不了力平衡点。

以下是对上面伪码的几个状态的进一步说明:

• VACANT:平衡点空，直接挪过去
• LOCKED:平衡点之前被挪过且被锁，尝试把待考虑点放到下一个空闲位置上，并且把abort_count加一，若加完abort_count>=aort_limit,则释放所有被锁点。
• SAME_AS_PRESENT_LOCATION:恰好平衡点就是现位置。视为这个位置空闲，占掉就行。
• OCCUPIED:这个点被占但并未被锁，那么就占领此点，转而考虑被踢出来这个点。

总结以下就是，最内层是寻找某点平衡点的过程，像是”连带反应“，但只存在于“这个位置不空，但没锁可以抢占”。其余任何情况都直接处理，退出循环。最外层循环遍历布局中各点，对每个点而言，尝试寻找iteration_limit次平衡点。

4.3.3 模拟退火(Simulated Annealing)

模拟退火算法(3.5.3节)是很多有名的放置算法的基础。

如图，算法在第2行给出一个初始解，然后做扰动(第5行),若有改善则接受扰动(7-8)，否则视变坏情况以一定概率接受扰动(9-12),在温度$T$下平衡之后，则降温，给$T$乘以一个小于1的系数，进入循环继续扰动并判断是否接受。这些步骤一直重复知道$T$下降到小于等于$T_{min}$

森林狼算法(TimberWolf)

森林狼算法由加州伯克利的C. Sechen提出，大致分三步:
1,模拟退火得出能降低线长的大致解
2,使用整体布线，进一步优化
3,以最小化通道高度为目标进一步局部地优化布局。

书上这一章只讨论了第一步，即模拟退火得出大致解的方法。
扰动。扰动是不断获得新的可能更优解的方法。森林狼算法的扰动有以下三种:

• 移动(MOVE),把某个单元挪到一个新的位置上。
• 交换(SWAP),交换两个单元的位置。
• 镜像(MIRROR),沿y轴把某一行进行翻转，仅当前两种方法都无效时才这样尝试。

这里森林狼算法对移动和交换的距离有一定限制:

某个单元只允许移动到以他为中心的宽，高为$w_T,h_T$的"窗口"范围内，交换也只允许交换满足以下关系的单元:

此处窗口大小和温度$T$挂钩，具体的来说，是与$log(T)$成正比。

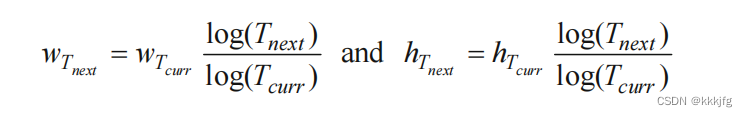
损失函数(Cost),这个算法的指标分为三部分，即线长，重叠，和行与行的长度差。
即$\Gamma ={\Gamma }_1+{\Gamma }_2+{\Gamma }_3$
${\Gamma }_1$是线长的加权和，这里使用半周长线长(half-perimeter wirelength (HPWL))来计算线长。$w_H$和$w_V$是对应网线在横向和纵向的权重。对于同一个网线，若$w_H(net1)$比$w_v(net1)$权重高,则表示更鼓励使用纵向的布线资源，要尽量节省横向布线，对于不同的网线，$w_H(net1)，w_v(net1)$比$w_H(net2)，w_v(net2)$表示给net1一个更高的优先级应该尽量减小net1的线长。

${\Gamma }_2$是重合面积。这里给了个平方，以对更大的重叠采取更大的惩罚。

${\Gamma }_3$就是每行的行长与目标行长的差距和了，之所以要约束这个，是因为参差不齐的行长会带来一些空间浪费和不均匀的线的分布，这样会提高布线拥挤程度和增加线长。

温度下降(Temperature Reduction)
大概概括一下森林狼算法的温度下降策略:先快($\alpha =0.8$),再变慢微调($\alpha =0.95$),在加快淬火($\alpha =0.8$)，T初始值在$4\cdot 10^6$,$T_{min}$取1。

内循环的次数(Number of Times Through the Inner Loop)
这里指在一个温度下执行扰动的次数，即如何判定在一个温度下达到了平衡。森林狼算法设置为每200个单元多循环100次，或者每个温度下执行$2\cdot 10^4$次。有的算法用接受扰动的比例来判断是否平衡。比如本章后面参考文献4.20中，Lam用了44%这个比例达到了不错的效果。

4.3.4 现代的摆放算法(Modern Placement Algorithms)

为适应需求变化，主流的摆放算法变过好几次。
现在的方法大多使用数值优化的方法优化目标函数，并在初始时忽略形状大小等因素，得到一个大致解，并在随后逐步把这些因素加入优化的目标进行优化。
范式主要有两种，就是前面说过的基于二次函数优化的放置和力导向的放置，以下是他俩的对比:

	基于二次函数优化的放置	力导向的放置
速度	快	慢
实现难度	能适应不同大小的系统，较简单	较困难，需要小心地微调以达到数值的稳定
条件利用程度	对形状大小等参数有所忽略，需要在运行过程中穿插“扩散”地步骤	能更好地考虑形状，大小等参数

影响二次函数优化的放置的一些关键:
1,网络建模
指前面提过的星状网、完全图等用于计算多引脚网络的模型。
完全图由于不引入新的变量，更适合小网络
星状网的线数随着规模是线性增加的更适合大网络。
2,扩散算法的选择。
3,优化二次函数和执行扩散算法的穿插策略。

二次函数优化一些细节与优化:
1,可以给每个线长平方$(x_i-x_j{)}^2$的权重加一个$1\frac{1}{x_i-x_j}$,以更贴近“缩短线长”的目标。权重在每轮之间进行更新。
2,可以穿插扩散和二次函数优化过程，并把每次扩散后的点视作“锚点”，对点给一个拉力，这样有助于把一堆模块扯得开一点，能减少重叠。

对于基于分析式的方法而言，可以在优化线长之外，加入布线拥挤程度等指标进入目标函数。

4.4 合法化和详细放置(Legalization and Detailed Placement)

由于在整体放置中，把各单元的坐标都看成是连续坐标了，而实际上电路中的逻辑门位置是离散的，所以我们需要把这些摆放合法化。合法的摆放应当是各模块在允许的行中等距摆放。全局摆放后的点坐标会被放到离它最近的合法位置上。
而且合法化不仅仅是在最后一步才做，也在物理合成(physical synthesis)的每一步增量修改后做，比如修改大小，插入新的模块之类。

不像全局摆放的时候的扩散操作，合法化的阶段是默认假设模块与模块之间的重叠很小的，所以它会直接把模块放到最近的合法位置上，然后使用详细放置进行进一步的优化(比如换位，或者把某一行的所有模块全推到一侧来减少空间浪费)。
由于把具体模块放到具体位置上了，所以可以做布线，所以有的布线器会在详细布置阶段进行可布线性分析。

这是一个图片例子，说明门电路在板子上是整整齐齐无重叠，一个萝卜一个坑地排放的。

一个较简单的合法化算法是D. Hill发明的"俄罗斯方块算法(Tetris)"，它把摆放后的各模块根据x坐标进行排序，依次放进最近的合法位置。这样做显然是比较粗糙的，比如当整个电路板比较空，而在板子两端都有输入输出端口的时候，用最简易版的俄罗斯方块算法可能会把电路单元全挤在了一侧，离另一侧的端口较远的情况。

俄罗斯方块算法有一些变种，比如先把整个电路板分成几块，然后分别实施俄罗斯方块算法，以避免挤成一堆和有些线过于长。还有的变种在寻找合法位置的时候把线长也纳入考虑，还有在模块间插入空挡而非紧密排列的做法，以求减少布线拥挤度。

有些合法化算法适合整体摆放同步进行的，例如在基于分割的摆放中，当分割块分割到足够小(如4-6个单元)的时候,可以直接穷举得到具体的摆放方案。或者在基于分析式的摆放方法中，也可以通过在迭代若干轮之后先固定最接近合法位置的一些模块，再迭代之后再固定另一批，这样边优化边找合法位置。

简单直接的合法化方法有时候会造成部分模块挪动较大距离，导致线长增加，这可以在详细摆放阶段缓解，比如可以设置一个滑动窗口，并在充分考虑外部连接的情况下对窗口内模块进行微调和排序操作，或在一行内进行重排。

还可以在划出窗口后继续划分左右半，交替进行重排和调整。

还有的手段通过对调进行优化，比如可以把导线连接的单元对进行调换，或者导线连接的三个单元进行循环调换，以尝试优化线长。也可以试着把挤在某一行一侧的单元挪到这一行的另一侧或者中间，以尝试进行优化。

合法化操作有时候和整体摆放经常在一块进行，比如ECO-System算法，也有的算法的合法化操作是相对独立的模块，比如 FastPlace-DP 算法。