第五章 Global Routing [VLSL Physical Design 学习笔记 ]

本文是对EDA教程《VLSL Physical Design》第五章的理解和笔记，对原文进行了翻译，评论和删减，若有谬误欢迎探讨和指出

5.1 简介

全局布线的过程，要把电势相同的引脚连起来。
具体而言，过程包括:
1,划分出路由区域
2,路由寻路
3,解决不同网络之间竞争资源的问题

网络(net)在这里指的是相互连接的有两个或以上有着相同电势的引脚集合。
通常来说，一个p引脚网络有一个扇入和p-1个扇出。

在有限面积内进行布线，有时某些线路需要绕行，或增加面积。

对于固定管线布线来说，由于模块位置固定，且不能加轨道数，不能保证百分百成功。
而对于可变管线布线来说，可以通过修改布局，插入管线等方式进行调整，通常能成功。

下图说明了布线的各个步骤都在干些什么。

如图，布线大致可以分为三步:
全局布线，详细布线和时序分析驱动的布线。

布线是在摆放已经大致固定的情况下把应该连的线连起来，但全局布线和详细布线是分为两阶段解决这件事。全局布线忽略具体的把线放在轨道上的活儿，只需要在每个区域的横纵轨道数限制下决定线大致从哪个区域穿到哪个区域即可。详细布线则只需要专注于一小块区域，把连线映射到具体轨道上。

对于模拟电路、多芯片模块（MCM）和印刷电路板，有时涉及网络较少，就只进行详细布线，不分成两步进行全局布线。

5.2 术语和定义

布线轨道。指的是水平/竖直的导线，信号网络往往由不同横纵导线层组成。相邻层之间的通信用通孔(vias)连接。

布线区域。指的是一个拥有布线轨道资源的区域。

均匀布线区域。指的是网格状排列的布线区域。布线区域大小形状相似，像网格一样排列在布局中。一个布线区域往往有7-40轨道宽，这个大小是平衡了芯片尺度上的全局布线的复杂度和区域尺度的详细布线的复杂度而定的。

非均匀布线区域。这通常是由于区域碰到了布局的边缘，或者具体电路板块的边缘所以不能按原大小形状走。这种区域往往需要使用交换盒(switch box)。

通道。指一个矩形布线区域，仅两个对侧(通常是长边)有引脚，另外两边没有引脚。
垂直通道指左右有引脚的通道，水平通道指上下有引脚的通道。

在传统的通道模型中，当布量大时，要扩展通道高度以容纳更多的轨道。但现在可以堆叠层数，所以这个规律有点失效了。

对于多层寻路而言，通道的容量为各层层高除以轨道间距。$h$和$d_{pitch}$如下图所示:
对于交换盒来说，它的尺寸更加固定和不灵活，通常它的入口位置固定，问题在于在这块区域内把路给找着。

下图是2D交换盒与3D交换盒，通道的示例。

如图，2D交换盒通常位于1，2，3金属层，通常是在前后左右有端口，3D交换盒通常在前后左右上下都有端口口，位于4，5金属层。
图我其实没看明白1，2，3层那些浮块都是啥，我猜是一个个的电子元件模块，然后金属线会在模块间进行走线，但由于没有高过这些元器件，所以不会出现顶或者底部对着元件的情况，故只有四侧有端口，高一些的金属层想和下面联络只能是靠上下端口。不过这样想的话下面的1，2，3金属层的交换盒其实也可以向上开口和上面交流？

T形结。指如下图所示的T形路口的交换盒:

在这种位置，竖直通道要先布线，书上给的理由如下:
1垂直通道的高度和水平通道的固定引脚的位置仅在垂直通道已经被布线之后才被确定。因此,垂直通道必须先于水平通道布线。
这里没完全get到什么意思，我猜意思是，如果横着的a,b,c在路过交换盒的时候，不能完全确定经过的纵线走的是哪个信号，所以要提前说好。不过反正最后是寻路算法算好就行了就知道通孔的位置了，所以如果我猜的意思是对的书上这里就相当于说了句废话？

5.3 优化目标

优化目标首先当然是保证线路的可布线性。在全局布线阶段，我们需要把线大致进行摆放，确保可布线性。
因为在详细布线阶段，只是在拥有有限轨道资源的布线区域内展开的，所以全局布线的时候不应该给某个布线区域太多的线以至于超过了资源量，全局布线应该在各个布线区域的横纵轨道数的限制下展开。
在此基础上，当然线长和延时是越低越好了。

以下内容不知道为什么给放到优化目标了，感觉像一些注意事项或者“顺带一提”。

全定制布局的布线

由于布局是高度定制的，所以会出现一些形状不固定的功能模块(macro cells),所以需要手动划分布线通道和定义通道的类型。
如下，布局中有A~F六个功能模块，然后可以把它如中间的布局树那样组织起来，从而定义了通道类型。比如A,B之间通过1号通道进行连线，A,D之间可以通过通道5进行连线。

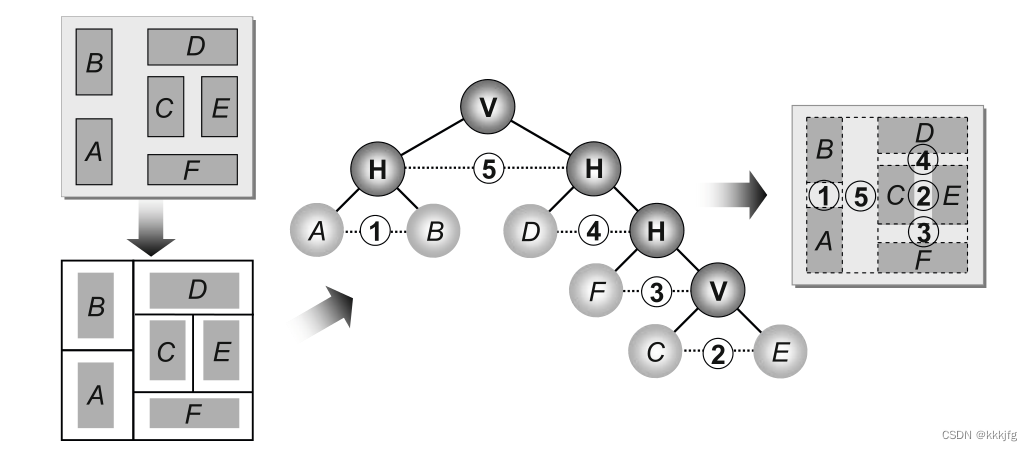
在定制化布局的布线中，定义好了布线区域之后，就可以使用Dijkstra等算法进行寻路了，且由于它是定制化的布局，可以调整通道宽度以容纳更多的布线，可以放更多的心思在减少线长和时延，不像固定版图的布局那样约束较多。

标准网格的布线

在标准网格的布线中，若金属层较少，则需要使用一些贯通单元($feedthroughcells$)来进行布线。
下图是贯通单元的示意:

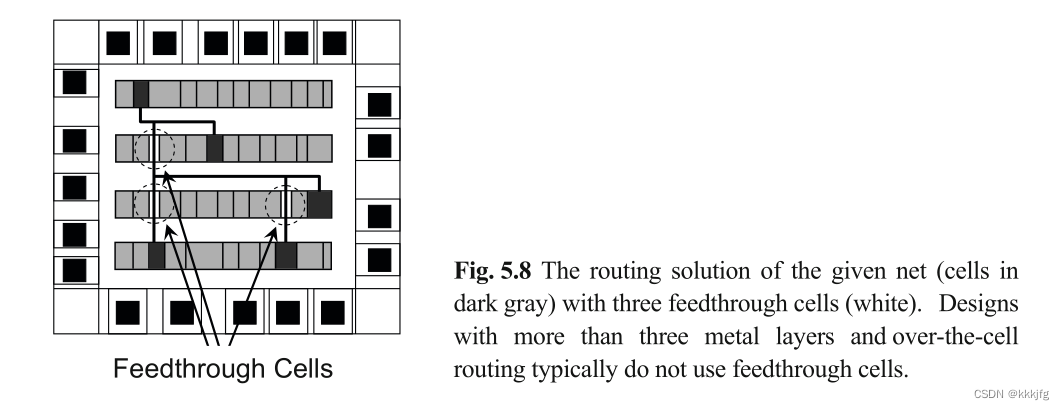
如箭头所指，有些本来可以放功能元件的单元直接被搬空贯通了，并用于布线。
存在这种设计是因为碰上金属层不够，不能换层进行布线，又要跨越单元行，而不得已需要删去一些可以做功能模块的单元用于布线。
这种情况下，由于布线资源的短缺性，布线的首要目标应该是布线成功，即可布线性，其次是减短线长。
若一个网络仅仅涉及一个路由区域，则它可以通过通道或者交换盒进行布线，但如果需要跨越布线区域，则网络需要进行切分和分配给不同的布线区域。这通常会使用斯坦纳树进行实现。

上图是两个连接5个点的斯坦纳树，左图线长最短，右图使用了最少的纵向线。

整个芯片的高度取决于功能模块的高度和加上通道的高度和，所以较短的布线往往会导致更紧凑的布局。

门阵列设计(Gate-array designs)

由于门阵列设计有着有限的布线资源，功能模块和布线区域都是固定的，轨道数也是确定的，不能插入额外轨道用于布线，所以其首要目标仍是保证可布线性和合理解，其次是缩短线长和减少延时。
下图是一个门阵列设计的例子，这个例子中，并非所有的网络都能被成功安置，网络C是布线失败的。

5.4 布线区域的表示(Representations of Routing Regions )

为了模拟布线过程，我们需要对布线区域进行建模建模，比如可以使用图的数据结构进行建模。
可以用点代表布线区域，边代表布线区域之间的连接区。不仅如此，由于每个布线区域的资源其实是有限的，比如横纵轨道数，所以建图的时候也应该把这些约束体现出来。

网格图(grid graph)

网格图可以定义为$ggrid=(V,E)$,其中$v\in V$代表一个布线网格($gcell$),一个边$e\in E$代表两个网格之间的连接。

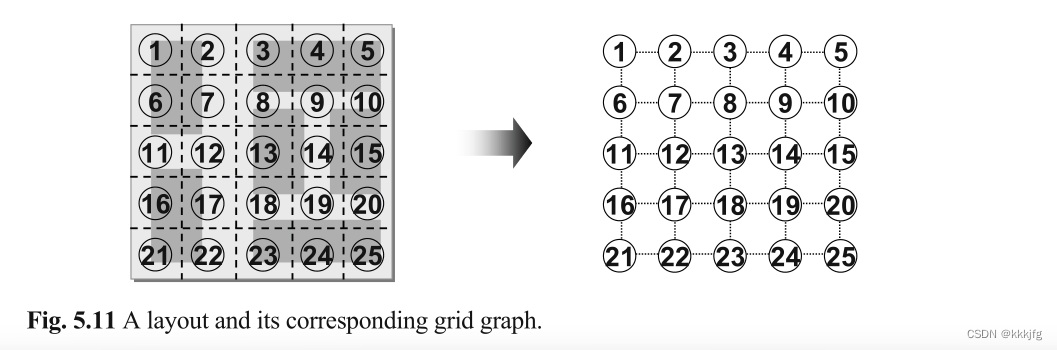
如果要表示横纵布线资源的话，可以用一个数对表示某个布线网格的资源量，比如可以用(3,1)代表有三条横向轨道和1条纵向轨道。值得注意的是，如果布线网格有多层，不同层之间的资源应该是独立的，故对于某个k层布线网格图，每个图节点应当保持k个不同的容量。

通道连通图(channel connectivity graph)

与网格图类似，不过在通道连通图中，节点$v\in V$代表的是通道

交换盒连通图(switchbox connectivity graph, or channel intersection graph)

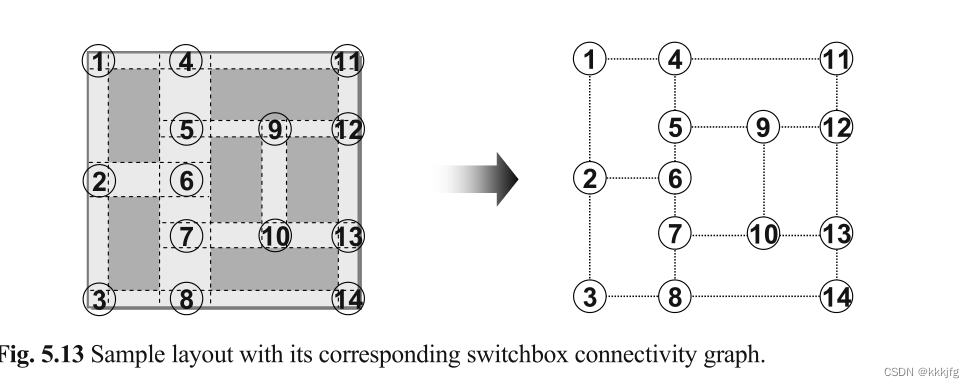
类似，$v\in V$代表交换盒，注意到这个图其实是把每个通道的两侧都放上了交换盒，比如T形连接处和十字路口，其实合理，因为这里是横纵线交汇的地方。我甚至觉得那个通道连通图没什么用，因为不知道那种横纵线交汇处怎么表示。所以自然，由于这里的交换盒都是放在通道两侧，所以图中的一个边可以代表一个通道。

5.5 全局布线的流程(The Global Routing Flow)

步骤1:定义路由区域。这一步的目的是对版图进行划分和建模，要把整个版图划分出一个个可以进行具体讨论的小的布线区域，搞清楚哪里要放通道，哪里要放交换盒，会建模成什么样的图。

步骤2:把网络映射到路由区域。这是一个有端口然后寻路并决定经过哪些区域以完成连线的问题。在寻路过程中，应该注意到每个区域的容量限制不能超了，并应当注意寻路的线长、时间延时等问题。

步骤3:交叉点分配。这个步骤是沿着布线区域把线路分配到固定点或者交叉点上(routes
are assigned to fixed locations, or crosspoints, along the edges of the routing regions.)。(我其实没完全get到这一段，猜测，意思是有的网络是跨区域的，若该网络在其中一个区域动了可能会扯到另一个区域的线，这里索性直接给它固定到区域交线上的某个点。这样每个区域最终就是独立的了不会相互影响而且可以并行计算)

需要注意有的交叉点对其他模块存在依赖关系，比如交换盒模块的交叉点需要四周的线都布好之后才能布置，有的全局布线算法并不执行交叉点分配这一步，而是让详细布线的一个叫“隐式交叉点分配”的步骤来做。

5.6 单个网络的布线(Single-Net Routing)

5.6.1 直角布线

这里主要介绍了两种给单个网络进行布线的方法，这个步骤中，输入是这个网络的各引脚，输出是走线方案。这里的两种方法都是把多引脚网络拆分，视作是多个双引脚网络，然后根据一定的顺序进行逐个击破。

直角生成树布线(Rectilinear spanning tree)。这里的Rectilinear不知道怎么翻译比较贴切，Rectilinear其实很形象，让人联想到矩形的，事实上它的意思确实是使用横纵线进行布线，在这种情况下寻找最小生成树。本方法不允许在引脚之外的额外点，什么叫“额外点”呢，就比如说，如果有两端线相交了，我们也不能把它们焊起来变成一个真正的导通的交点，只允许导线引脚这种点给电和允许导线之间的虚交。(这本书这里我估计是为了和下面的最小斯坦纳树方法区分开，所以不允许额外的交点，因为根据后面的讨论，额外的交点事实上有可能帮助进一步减少线长)。
该算法从单个点开始，贪心式地加入更多点，使用Prim算法构建的计算复杂度在$O(p^2)$,用现代的一些计算机几何技术的计算下，复杂度可以降到$plog(p)$

直角斯坦纳树布线(Rectilinear Steiner tree)。这里的“直角”含义和上面一样，斯坦纳树的意思是，允许在引脚之外，额外添加一些“斯坦纳点”作为基点纳入路径的计算(否则只是在引脚之间找连线)。斯坦纳点是什么?在这里可以理解为布好的线，或者两条线的交点上的一个可以用来寻路的起点。

如图，这是一个三引脚网络，如果不允许"斯坦纳点"，那么需要有p1-p2,p2-p3两条独立的线，p1-p2是一横一纵，p2-p3是一纵一横。但这里，额外设置了一个斯坦纳点S1，那么就需要S1-p1,S1-p2,S1-p3三条线。

斯坦纳树的一些性质:

• 一个斯坦纳树有0~p-2个斯坦纳点。
• 一个斯坦纳树的端点的度是1~4，斯坦纳点的度是3 ~ 4

根据我的搜索，这本书的“斯坦纳树”相关概念好像还不是其最原始的意思，B站上有个说斯坦纳树的教程我觉得还不错：https://www.bilibili.com/video/BV1HG411A7fM

构造最小斯坦纳树是一个NP难问题，在实践中往往采用启发式方法。由C.Chu和Y.Wong开发的一种快速技术FLUTE可以为九个引脚以内的网络找到最佳的斯坦纳树，并为较大的网络产生接近最小的斯坦纳树，通常只超出最优解1%的以内。尽管最短的斯坦纳树在线路长度方面是最优的，它们并不总是在实践中的网络布线的最佳选择。

由于某些生成斯坦纳树的启发式算法不能很好的避障，或者响应某些需求(比如优化指定路径的用时)，有时候会使用直角最小生成树来布线，且这样做的代价不会超过1.5倍的最小斯坦纳树的解。这里举一个最坏的1.5倍的情况:(0,1),(0,-1),(-1,0),(1,0)四个点，用最小生成树生成三段网线，总长为6，而斯坦纳树可以在(0,0)处放一个斯坦纳点，这样代价是4。

上图是斯坦纳树，最小生成树两者的对比，以上斯坦纳树的生成过程是，在p1~p2之间连线并尝试上下两条线路，p2 ~p3同理，然后选择重合度最高的一组线路，即可得到$S_1$。

Hanan网格 。前面提到的例子说明了最小斯坦纳树是怎样减少线长的，M.Hanan在1966提出了一个算法，可以快速构建质量还不错的斯坦纳树。他发现就斯坦纳点来说，仅仅考虑由引脚延申出的横纵线构成的网格的交点即可，这样就能构成一个还不错的解。也就是对于每个点$(x_p,y_p)$，我们都引两条线$x=x_p$和$y=y_p$，如此构成网格。只需要在这些网格的交点上进行选择即可。这样对于p个引脚的网络只有$p^2$这么大的搜索空间。
以下是一个Hanan网格的例子,这个例子中构建网格后选择了中间的两个点作为斯坦纳点构建了斯坦纳树。

定义布线区域
在斯坦纳树的全局布线中，往往把通道划分成一个粗略的布线网络。由于尚不清楚通道高度，距离由横向距离代替。引脚被假设放在网格中央。示意图如下:

启发式的斯坦纳树构造算法
以下启发式算法使用Hanan网格来生成一个接近最小化的直角Steiner树。该启发式算法贪心地建立新连接，使其与树拓扑结构兼容（回想Prim最小生成树算法），并尽可能保留边的嵌入灵活性(此处嵌入方式指的是“嵌入平面的方式”，即方向和位置，此处保留嵌入灵活性就是保留边的可选择性，希望不是寻路过程中一下子就给固定死，留一定灵活性能给往后的启发式搜索留下更多寻找更优解的空间)。对于最多有四个引脚的网络，此启发式算法总是产生最小斯坦纳树。否则，产生的直角斯坦纳树不一定是最小的。

这个算法的伪码如下:

算法从整个图中最近的两个点开始(第2-4行)，若整个图就俩点，则连线结束算法(7-8)。
否则，维护一个矩形框curr_MBB(10,20)。每次找$p^{\prime }$集里与curr_MBB最近的点，并从curr_MBB到$p^{\prime }$连一条线。
此线在curr_MBB的端点在哪一侧就保留curr_MBB哪一侧(18-19)，若不在线段上在端点上，则随便保留一侧(16-17)。
下面是一个例子。
curr_MBB可以理解为一个半连上的线，已经确定了是他俩连起来，但仍留一定空间用来调整。


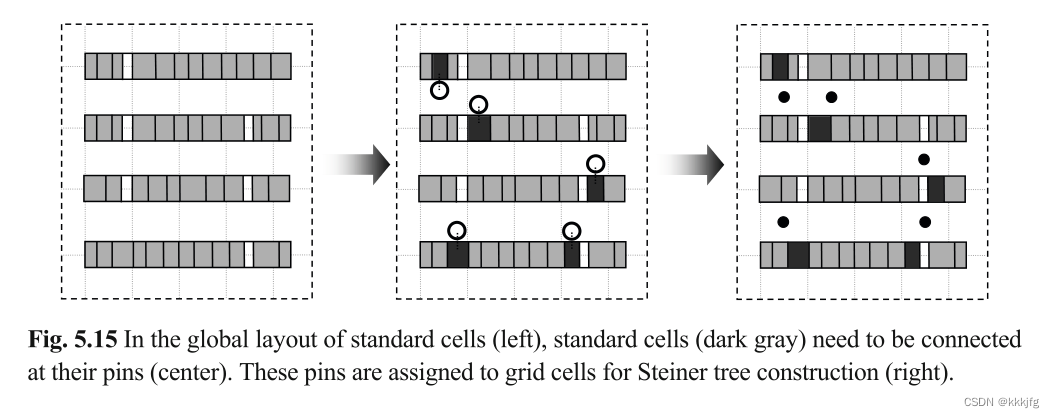
将网络映射到路由区域(Mapping nets to routing regions)。在为网络找到合适的斯坦纳树后，要将各分段映射到物理布局上。每个网段被分配给一个特定的网格单元(如下图右侧所示，每个灰色布线区域都被分配了一段网络)。在进行这些分配时，还考虑了每个网格单元的水平和垂直容量。

5.6.2 连通图中的全局路由算法

连接图上的几种全局路由算法基于Rothermel和Mlynski在1983年引入的通道模型。该模型结合了交换机和通道，并处理非矩形块形状。它适用于全定制设计和多芯片模块。连接图中的全局路由是使用以下步骤序列执行的。

1，定义布线区域。布线区域是通过在每个方向上拉伸功能单元的边界框直到边界而形成的。

2，定义连通图。连通图中，节点代表路由区域，两个节点之间的边表示这些路由区域是连接的。每个节点还维护其路由区域的水平和垂直容量。

3,确定网络顺序。可以在布线之前或之时确定处理网络的顺序。可以根据关键性、引脚数、包围框大小（较大表示优先级较高）或电学特性等对网络进行优先级排序。一些算法根据路由尝试过程中观察到的布局特征动态更新优先级。

4,为所有引脚连接分配轨道。对于每个引脚，在引脚的路由区域内保留一个水平轨道和一个垂直轨道。
这一步是为了确保引脚可以连接。
它还提供了两个主要优点。
1)首先，因为引脚连接的轨道分配是在全局布线之前执行的，如果引脚不可访问，则必须调整单元格的放置。
2)其次，轨道预留可以防止先路由的线路阻碍稍后使用的引脚连接。这为路由器提供了更准确的拥塞图，并让未来的网络能更好的的绕路。

5,全局布线所有网络。每个网络按照预先确定的顺序分别处理。对于每个网络，将应用以下步骤：

5.1网络和/或子网的排序：将多引脚网络分成双引脚子网，然后通过对每个子网的引脚进行排序（例如，按照x坐标的非递减顺序），确定一个适当的顺序。
5.2在连接图中进行轨道分配：使用迷宫型路由算法（第5.6.3节）为轨道分配，使用区域的剩余资源作为权重。区域内若拥塞则会鼓励路径绕至低拥塞的区域。
5.3在连接图中进行容量更新：在找到路径后，每个区域的容量会在相应的节点上相应减少。

值得注意的是，水平和垂直容量是分开处理的。即，垂直（水平）布线路径不会影响同一区域的水平（垂直）容量。

下图是一个在连通图内布线的例子。

5.6.3 用Dijkstra算法求最短路径(Finding Shortest Paths with Dijkstra’s Algorithm)

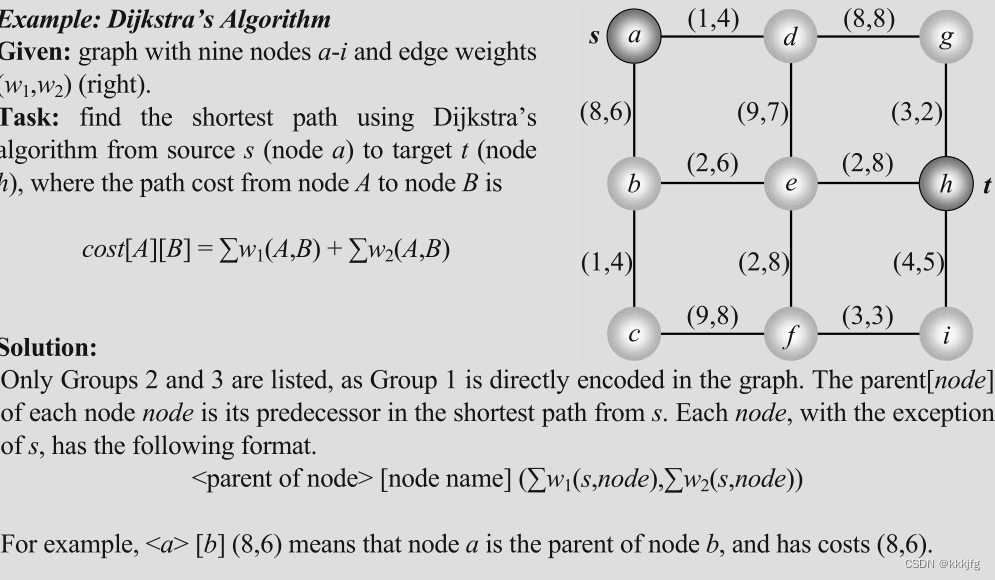
Dijkstra算法太经典了，此处略过文字解析部分，以下是一个在连通图运用Dijkstra算法寻路的例子:

5.6.3 用Dijkstra算法求最短路径(Finding Shortest Paths with A* Search)

与Dijkstra一样，A算法也是经典寻路算法，与Dijkstra相似，它也是每次让最有潜力的节点出队，不同的是Dijkstra仅根据与源节点的距离决定下一个搜谁，A算法还结合了与目标节点的距离作为出队依据。具体细节网上教程很多，这里不再赘述。
下图是BFS+Dijkstra与A*算法的对比。

5.7 所有网络共同寻路(Full-Netlist Routing)

前面说的仅仅是单网络进行寻路，所有网络一块儿的话会让这件事变得复杂一些，比如我们需要确保各网络不会打架，或者说不会过度拥挤地占用某些资源导致不能布线。且同时我们需要尽量缩减布线长度和减少延时。

如何办到让所有寻路这件事呢？前面已经提过一种方法就是用某种评价指标给各网络排序，让重要的网络先布线，后布线的网络再绕路。

后面还会介绍两种方案,一种是，同时考虑所有网络，另一种是一个个布网络，到后面遇到冲突了再看看谁不合适，挑开重布。

5.7.1 利用整数线性规划进行布线(Routing by Integer Linear Programming)

线性规划(Linear Programing, $LP$)由一组约束和一个目标函数组成。这个函数的最大化或最小化取决于这些约束条件。约束条件和目标函数都必须是线性的。这些约束形成了线性方程组和不等式。整数线性规划(Integer Linear Programming,$ILP$)是一种线性规划，其中每个变量只能假设为整数值。所有变量都是二进制的$ILP$称为0-1 ilp。线性规划可以使用各种可用的软件工具来求解，如GLPK, CPLEX和MOSEK。有几种方法可以将全局路由问题表述为ILP，下面介绍其中一种方法。

整数线性规划的输入是:
(1)布局的网格图G
(2)网格图各线的资源量
(3)待布线的网络列表
G中水平边从左到右是G(i,j) ~ G(i+1,j)，垂直边从上到下是- G(i,j) ~ G(i,j+1)。

整数线性规划中，每一个网络有两组变量，第一组有k个变量$x_{net1}$,$x_{net2}$,$x_{net3}$……$x_{netk}$，这里k的含义是有k种可选择的路线。这k个变量里有一个是1，其余是0，代表选择了某一个。第二组变量是$w_{net1}$,$w_{net2}$,$w_{net3}$……$w_{netk}$,这组变量代表权重，显然，越小权重的选择越被鼓励使用。
当整个布局有$|Netlist|$个网格的时候，就一共有约$k\cdot |Netlist|$个变量。

这个线性也两组约束,一是每个网络只能在众多选择中选择一种，所以k个选择变量只有一个是1，其余是0。第二组变量是线路的资源约束，即各网络使用图的点、边要在其布线资源允许范围之内。

上图是整数线性规划的不等式组，围绕网络的选择的约束，与各边的容量约束展开。
网络的选择的约束描述了每个选择只可能是1或者0，即选或不选，且所有选择只有一个能选所以只有一个1.
各边的容量约束就是穿过图上的某边的网络数目不能超过容量。

那么有一个问题是:怎么确定每个网络的k个选项的呢?讲道理一个点寻路到另一个点的方案应该是非常非常多，难道要全部纳入考虑吗？实践中，往往使用一些简单网络作为选项，比如不是正对着的引脚可以使用L形线，正对着的引脚可以使用直线，U形线作为选项。这样很难保证每个网络都能找到路，这样做完之后没有安置好的网络可以使用迷宫布线算法如Dijkstra和A*算法进行寻路。

基于ILP的全局路由器包括Sidewinder和BoxRouter 1.0。两者都使用FLUTE将多引脚网络分解为两个引脚网络，并且每个网络的路由从两个备选方案中选择或未选择。Sidewinder在某个网络的两个选项都不成功的时候，会执行迷宫寻路算法，替代一个选项的失败的路线。另一方面，它可以从选项中移除已成功路由且不干扰未路由的网络的网络。因此，Sidewinder会替代和反复进行整数线性规划，直到没有观察到进一步的改进。相比之下，BoxRouter 1.0使用迷宫路由技术对其ILP的结果进行后期处理。

以下是一个例子:

5.7.2 撤销并重新布线(Rip Up and Reroute, RRR)

现代整数线性规划解算器性能已经很强劲了，基于整数线性规划算法的全球路由器能在数小时内成功完成数十万条路由。
然而，商业EDA工具仍需要更大的可扩展性和更低的运行时间。这些性能要求通常使用撤销并重新布线(RRR)框架来满足，该框架针对布线失败网络。如果网络无法布线，这通常是由于物理障碍或其他路由网络阻碍。
关键思想是临时允许冲突，这样所有网络都能寻路，但随后会迭代地删除一些网络(撤销)，并以不同的方式进行寻路，以减少冲突次数。、

前面提过一种直观、贪心的算法，即按顺序对网络进行寻路，但这样后进行寻路的网络可能需要绕很大的弯路。

而RRR框架允许网络暂时超容量进行路由。这有助于决定哪些网络应该绕行，而不是绕行最晚路由的网络。在下图图a的示例中，假设网络按照基于网络的纵横比和MBB的大小的顺序进行路由(顺序为A-B-C-D)。如下图图b， 如果每个网络的路由没有违规，则网络D被迫绕行很长的距离。

如上图，中间的就是按顺序布线的结果，而上图图把ABCD都布了个遍，然后发现B重布的代价最小，就撤销B的布线进行重布。

传统的RRR策略依赖于(1)冲突下撤销和重新布线的质量，以及(2)网络布线顺序的确定。也就是说，网络的布线顺序极大地影响了最终解决方案的质量。例如，Kuh和Ohtsuki在1990年为每个违反规定的网络定义了可量化的针对每个网络RRR成功率，这样就可以只对最有希望的网络进行撤销和重新布线。然而，只要网络重新布线失败，就会再次计算网络的布线成功率，这又运行时间增加，尤其是对于大规模电路设计。

如图，算法会把所有有冲突的网络都放入队列(4-5行)，然后，每次把所有冲突重布，直到所有网络都已经可以布好(第6行)。
具体来说，怎么处理所有冲突呢？每次要根据需求把冲突的网络进行排序(第9行)，一个个取队头元素若还有冲突(第10行)就进行重布(第9行)并出队(第15行)，若还有冲突就再放进队列等待下一轮重布(第13-14行)。

请注意，在这个RRR框架中，并不是所有的网络都必须被重布。为了进一步减少运行时间，可以选择性地选择一些冲突的的网络使它们暂时不被撕毁。这通常会导致线路长度少量增加，但会大量减少运行时间。在协商拥塞路由的情况下(第5.8.2节中会提到)，网络会被撤销并重新路由，并且适当记录拥塞边的历史成本(history costs，这里大概是指布线成本或者冲突的惩罚函数成本？)。维护这些历史成本可以提高撤销和重新路由的成功率，并降低对高质量的排序的依赖。
(这段关于历史成本的内容个人不能完全理解，不知道历史成本能有什么用，也许可以作为某种数据用来预测下一步应该重布谁)

5.8 现代的全局布线技术(Modern Global Routing)

随着芯片规模的增加，芯片布线长度和通孔数量应该进行限制以提升芯片的性能，功耗。
全局布线形成无冲突的布线很重要，完成了它能够更好过渡到后续的详细布线，或者进一步面向可生产的布线进行优化。
如果实在无法布线，需要更改布局，摆放的话，可以隔离问题区域，填充一些空白区域到拥挤区以减轻拥挤。

有些著名的布线器如FGR, MaizeRouter, BoxRouter, NTHU-Route 2.0 NTUgr, FastRoute 3.0等，于2007-08年提出，各自在速度与质量之间有自己的平衡。

以下是一个标准的全局布线的流程，从一开始的初始化，分解多引脚点为多个双引脚点，然后给出初始的布线解，不冲突直接就进一步把2维的布线映射到多层的三维的网格上了，若冲突则进行撤销重布(有的布线器会在撤销重布之后进一步进行“清理”步骤优化线长)，直到没有冲突。
也有布线器直接在三维网格上进行寻路以尽量缩短最终的线长，但这样时间成本较高，且失败几率更高。

5.8.1 模式布线(Pattern Routing )

给定一组包含两个引脚的网络，全局布线器必须在遵守容量限制的前提下为每个网找到路径。为了最小化线长，大多数网都使用短路径进行布线。可以使用迷宫布线技术，如Dijkstra算法和A*搜索，来保证两点之间的最短路径。但是，这些技术可能会显得比较慢，特别最优解事实上只需要很少的转弯时，例如L形。在实践中，许多网的路线不仅是短的，而且弯曲很少。因此，很少有网络需要迷宫布线器。
为了提高运行时间，模式布线会搜索一小部分布线模式，或者说叫套路。它经常会找到很短的路径，从而使迷宫布线不必要。给定一个$m\times n$的边界框，其中$n=k\cdot m$，$k$是一个常数，模式布线需要$O(n)$的时间，而迷宫布线需要$O(n^{2}log(n))$的时间。
在模式布线中常用的拓扑包括L形、Z形和U形(如下图所示)。

5.8.2 协商拥塞布线(Negotiated Congestion Routing, NCR)

什么是协商拥塞布线？让我用一句话概括，我会说，是动态调整各边的权重以更多地惩罚跑到拥挤区域的线。
那么这样做的好处是什么呢？举个例子，由于Dikstra，A*算法之类的布线会找代价和最小的路进行布线，

若适当提高拥挤区域的布线的惩罚，就能让这些寻路算法尽量少地走这些区域，以避免出现冲突而后又进行撤销与重布线。
另外，布线的惩罚$cost(e)$并不会减小，而是在整个布线过程中单调增加或者保持不变，因为如果减小，会导致之前某些惩罚力度的路线失去惩罚，而回到原本的位置上。

上面地每条边的惩罚$cost(e)$与拥挤度$\varphi (x)=\frac{\eta (e)}{\sigma (e)}$挂钩，其中$\eta (e)$是当前状态下使用某边的网络数，$\sigma (e)$是其容量。

在NCR算法中，我们只在某线路的拥挤度大于1的时候才改变$cost(e)$,当$\varphi (x)<=1$时不作改变(感觉有点像“可以挤，但不能全挤在一起，要大致分开”的意思？)。并且每次进行布线之后，$cost(e)$会更新，这样边权发生变化，发生不同路同代价的概率会小一点，而寻路算法是按代价，重要性定优先级决定谁先布线的，同代价要进一步排序，所以这样可以一定程度上减少对排序算法的依赖。

$cost(e)$的增长速率比较有讲究，太快了容易把线从一边赶到另一边又赶回来，导致震荡。太低了又起不到效果，要更久才能达成没有冲突的布线。理想状况下，$cost(e)$应该逐渐增长，这样每次迭代都会有一部分的线重新布线。在实践中，有的网络把它建模成线性函数、动态的指数函数和sigmoid函数。经过良好调整的基于NCR的路由器可以有效地减少拥塞，同时保持较低的线路长度。

下图是一个使用了RRR技术的迭代过程中的冲突数和线长的变化图，可以看到它解冲突卓有成效，且不会增加太多线长。