关于交叉熵损失函数以及几个类似的损失函数

1. 交叉熵的定义

1.1 熵

对于概率分布，熵的定义是：

 熵度量了一个分布的均衡程度，分布越均衡，熵越大。

1.2.1 对熵的个人理解

        熵和能量是一对相对的概念。这个世界越有秩序，能量越大，熵越小；越无秩序，能量越小，熵越大。如果没有人为因素，世界是自动趋向于无序的，也就是熵会自动的越来越大，也就是自然界是熵增的。而人喜欢有秩序，人类不断发展的目的就是为了让这个世界遵循自己想要的样子变化（人类在迷茫的时候最喜欢问自己的一个问题是：你想要的到底是什么）。也就是人的本质是熵减的。所以，因为人的存在，对抗了自然界的熵增的过程。所以《道德经》有曰：“天之道，损有余以补不足；人之道，损不足以奉有余”

1.2 交叉熵

        熵的定义只针对一个分布，而交叉熵的定义是针对两个分布的。我们假设有两个分布：和。那么这两个分布的交叉熵就是：

这是离散的情况，如果是连续的情况，可以求和变成积分。变成了曲线下的面积。交叉熵度量了两个分布的差异的大小。p和q差异越大H(p,q)就越大，差异越小，H(p,q)就越小。当p=q时最小，此时交叉熵变为p的熵。有个动态图可以很直观的了解上面的意思：

链接:Cross Entropy动图

2. 关于softmax

上面我们看到，交叉熵是针对两个概率分布的，softmax最重要的作用就是把以串数字变换成一个概率分布。所以为了让神经网络最后能用上交叉熵损失函数，往往要在最后加一个softmax计算模块。

softmax的计算公式就是：

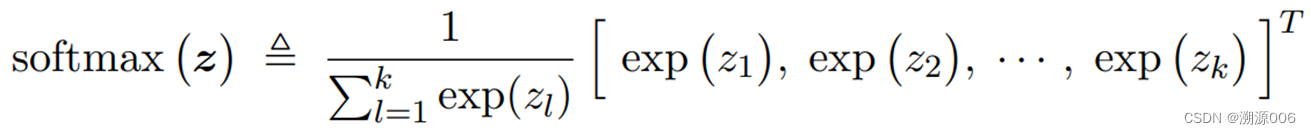
其中是一个任意的k维向量。如果用图直观的解释softmax的作用就是如下：

softmax把任意一个向量变成了一个同样维度的概率分布。

刚才说了交叉熵的计算需要两个概率分布，现在有一个是神经网络的输出，那么两一个分布是什么呢，另一个分布就是监督信号，或者叫做groundtruth，如下图所示：

所以最后对于一个样本的交叉熵损失函数的输出就是当前神经网络所预测的这个样本属于真实类别的自信息量：

如果把softmax也写出来就是

其中，是样本属于的那个类别。

这个损失函数的效果就是：经过梯度下降之后，神经网络的预测的概率分布与groundtruth更加接近，也就是这个样本被预测为真实类别的概率增加。也就是增加当观察到时，判定为类别j的概率。

3.其他几个损失函数与交叉熵损失函数的类比

3.1 InfoNCE损失函数

MOCO中用的InfoNCE损失函数：

MOCO论文地址：

这个损失函数的目的肯定就是经过梯度下降后，增加判定q与相似的概率。

3.2 基于策略的强化学习

可参考博主另一篇文章：

基于策略的深度强化学习：理论部分-CSDN博客

参考：

【1】什么是Cross Entropy (交叉熵)？ - 知乎