数学原理
假设源图像A大小为m*n,缩放后的目标图像B的大小为M*N。那么根据比例我们可以得到B(X,Y)在A上的的
对应坐标为A(x,y)=A(X*(m/M),Y*(n/N))。在双线性插值法中,我们选取A(x,y)的最近四个点。而在双立方
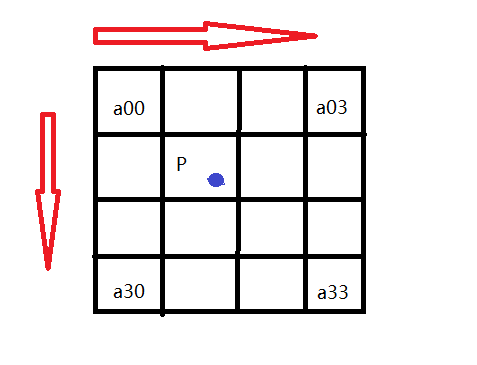
插值法中,我们选取的是最近的16个像素点作为计算目标图像B(X,Y)处像素值的参数。如图所示:
如图所示P点就是目标图像B在(X,Y)处对应于源图像中的位置,P的坐标位置会出现小数部分,所以我们假设
P的坐标为P(x+u,y+v),其中x,y分别表示整数部分,u,v分别表示小数部分。那么我们就可以得到如图所示的
最近16个像素的位置,在这里用a(i,j)(i,j=0,1,2,3)来表示。
双立方插值的目的就是通过找到一种关系,或者说系数,可以把这16个像素对于P处像素值得影响因子找出
来,从而根据这个影响因子来获得目标图像对应点的像素值,达到图像缩放的目的。
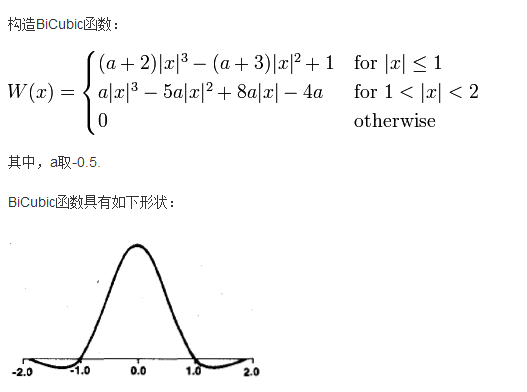
我在这次的学习中学习的是基于BiCubic基函数的双三次插值法,BiCubic基函数形式如下:
我们要做的就是求出BiCubic函数中的参数x,从而获得上面所说的16个像素所对应的系数。在学习双线性插
值法的时候,我们是把图像的行和列分开来理解的,那么在这里,我们也用这种方法描述如何求出a(i,j)对应
的系数k_ij。假设行系数为k_i,列系数为k_j。我们以a00位置为例:
首先,我们要求出当前像素与P点的位置,比如a00距离P(x+u,y+v)的距离为(1+u,1+v)。
那么我们可以得到:k_i_0=W(1+u),k_j_0=W(1+v).
同理我们可以得到所有行和列对应的系数:
k_i_0=W(1+u), k_i_1=W(u), k__i_2=W(1-u), k_i_3=W(2-u);
k_j_0=W(1+v), k_j_1=W(v), k_j_2=W(1-v), k_j_3=W(2-v);
这样我们就分别得到了行和列方向上的系数。
由k_i_j=k_i*k_j我们就可以得到每个像素a(i,j)对应的权值了。
最后通过求和公式可以得到目标图片B(X,Y)对应的像素值:
pixelB(X,Y)=pixelA(0,0)*k_0_0+pixelA(0,1)*k_0_1+…+pixelA(3,3)*k_3_3;
这里其实就是个求和公式,由于不知道怎么编辑公式,就这样表达了。
#include<opencv2\imgproc\imgproc.hpp>
#include<opencv2\highgui\highgui.hpp>
#include<opencv2\core\core.hpp>
#include<iostream>
#include<cmath>
using namespace std;
using namespace cv;
float BiCubicPloy(float x);
//BiCubic基函数
float BiCubicPloy(float x)
{
float abs_x = abs(x);//取x的绝对值
float a = -0.5;
if (abs_x <= 1.0)
{
return (a + 2)*pow(abs_x, 3) - (a + 3)*pow(abs_x, 2) + 1;
}
else if (abs_x < 2.0)
{
return a*pow(abs_x, 3) - 5 * a*pow(abs_x, 2) + 8 * a*abs_x - 4 * a;
}
else
return 0.0;
}
Mat BiCubicInter(Mat &srcImage, double kx, double ky)
{
//获取输出图像的分辨率
int nRows = cvRound(srcImage.rows*kx);
int nCols = cvRound(srcImage.cols*ky);
Mat resultImage(nRows, nCols, srcImage.type());
for (int i = 0; i < nRows; i++)
{
for (int j = 0; j < nCols; j++)
{
//获取目标图像(i,j)在原图中的坐标
int xm = i / kx;
int ym = j / ky;
//取出映射到原图的整数部分
int xi = (int)xm;
int yi = (int)ym;
//取出映射到原图中的点的四周的16个点的坐标
int x0 = xi - 1;
int y0 = yi - 1;
int x1 = xi;
int y1 = yi ;
int x2 = xi + 1;
int y2 = yi + 1;
int x3 = xi + 2;
int y3 = yi + 2;
if ((x0 >= 0) && (x3 < srcImage.rows) && (y0 >= 0) && (y3 < srcImage.cols))
{
//求出行和列所对应的系数
float dist_x0 = BiCubicPloy(xm - x0);
float dist_x1 = BiCubicPloy(xm - x1);
float dist_x2 = BiCubicPloy(xm - x2);
float dist_x3 = BiCubicPloy(xm - x3);
float dist_y0 = BiCubicPloy(ym - y0);
float dist_y1 = BiCubicPloy(ym - y1);
float dist_y2 = BiCubicPloy(ym - y2);
float dist_y3 = BiCubicPloy(ym - y3);
//k_i_j=k_i*k_j
float dist_x0y0 = dist_x0 * dist_y0;
float dist_x0y1 = dist_x0 * dist_y1;
float dist_x0y2 = dist_x0 * dist_y2;
float dist_x0y3 = dist_x0 * dist_y3;
float dist_x1y0 = dist_x1 * dist_y0;
float dist_x1y1 = dist_x1 * dist_y1;
float dist_x1y2 = dist_x1 * dist_y2;
float dist_x1y3 = dist_x1 * dist_y3;
float dist_x2y0 = dist_x2 * dist_y0;
float dist_x2y1 = dist_x2 * dist_y1;
float dist_x2y2 = dist_x2 * dist_y2;
float dist_x2y3 = dist_x2 * dist_y3;
float dist_x3y0 = dist_x3 * dist_y0;
float dist_x3y1 = dist_x3 * dist_y1;
float dist_x3y2 = dist_x3 * dist_y2;
float dist_x3y3 = dist_x3 * dist_y3;
resultImage.at<Vec3b>(i, j) = (srcImage.at<Vec3b>(x0, y0)*dist_x0y0 +
srcImage.at<Vec3b>(x0, y1)*dist_x0y1 +
srcImage.at<Vec3b>(x0, y2)*dist_x0y2 +
srcImage.at<Vec3b>(x0, y3)*dist_x0y3 +
srcImage.at<Vec3b>(x1, y0)*dist_x1y0 +
srcImage.at<Vec3b>(x1, y1)*dist_x1y1 +
srcImage.at<Vec3b>(x1, y2)*dist_x1y2 +
srcImage.at<Vec3b>(x1, y3)*dist_x1y3 +
srcImage.at<Vec3b>(x2, y0)*dist_x2y0 +
srcImage.at<Vec3b>(x2, y1)*dist_x2y1 +
srcImage.at<Vec3b>(x2, y2)*dist_x2y2 +
srcImage.at<Vec3b>(x2, y3)*dist_x2y3 +
srcImage.at<Vec3b>(x3, y0)*dist_x3y0 +
srcImage.at<Vec3b>(x3, y1)*dist_x3y1 +
srcImage.at<Vec3b>(x3, y2)*dist_x3y2 +
srcImage.at<Vec3b>(x3, y3)*dist_x3y3 );
}
}
}
return resultImage;
}
int main()
{
Mat srcImage = imread("lakeWater.jpg");
if (!srcImage.data)
{
printf("image could not load...\n");
return -1;
}
imshow("srcImage", srcImage);
Mat resultImage = BiCubicInter(srcImage, 0.5, 0.5);
imshow("resultImage", resultImage);
waitKey(0);
return 0;
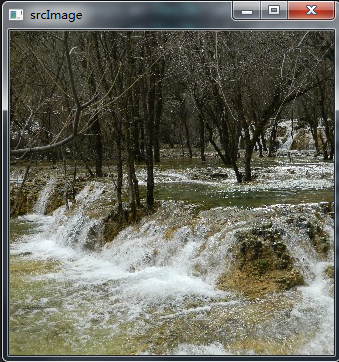
}原图:
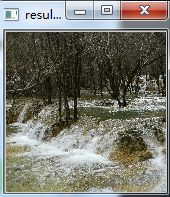
效果图:
























 2万+
2万+

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








