激活函数(重新使用Matlab画了函数图像)
1.介绍
激活函数(Activation Function)层又称非线性映射(Non-Linearity Mapping)层,作用是增加整个网络的非线性(即表达能力或抽象能力)。深度学习之所以拥有强大的表示能力 ,关键就在于激活函数的非线性
然而物极必反。由于 非线性设计 所带来的一系列 副作用(如 期望均值不为0、死区),迫使炼丹师们设计出种类繁多的激活函数来 约束 非线性 的 合理范围
由于激活函数接在BN之后,所以激活函数的输入被限制在了 ( − 1 , − 1 ) (-1,-1) (−1,−1)之间。因此,即使是ReLu这种简易的激活函数,也能很好地发挥作用
2.函数类型
Sigmoid类
1.Sigmoid
Sigmoid函数,即著名的 Logistic 函数。被用作神经网络的阈值函数,将变量映射到
(
0
,
1
)
(0,1)
(0,1)之间
S
(
x
)
=
1
1
+
e
−
x
S(x)=\frac{1}{1+e^{-x}}
S(x)=1+e−x1

缺点:
(1)输出值落在 ( 0 , 1 ) (0,1) (0,1)之间,期望均值为 0.5 ,不符合均值为 0 的理想状态(2)受现有的梯度下降算法所限(严重依赖逐层的梯度计算值),Sigmoid函数对落入 ( − ∞ , − 5 ) ⋃ ( 5 , ∞ ) (-\infty,-5)\bigcup(5,\infty) (−∞,−5)⋃(5,∞)的输入值,梯度计算为 0,发生梯度弥散,因此该函数存在一正一负两块“死区”
2.HardSigmoid
对HardSigmoid和Sigmoid的比较表明,HardSigmoid无论是以特定的硬件形式实现还是以软件形式实现都具有较小的计算代价,并且作者强调了它在基于DL的二进制分类任务中显示出的一些有前途的结果。
H
S
(
x
)
=
m
a
x
(
0
,
m
i
n
(
1
,
x
+
1
2
)
)
HS(x)=max(0,min(1,\frac{x+1}{2}))
HS(x)=max(0,min(1,2x+1))

Tanh(x)类
1.tanh(x)
tanh是双曲函数中的一种,又名双曲正切
t
a
n
h
(
x
)
=
2
S
(
2
x
)
−
1
=
e
x
−
e
−
x
e
x
+
e
−
x
tanh(x)=2S(2x)-1=\frac{e^x-e^{-x}}{e^x+e^{-x}}
tanh(x)=2S(2x)−1=ex+e−xex−e−x

改进:
将期望均值平移到了0这一理想状态
缺点:
本质上依然是Sigmoid函数,依然无法回避一左一右两块 “死区”(此时“死区”甚至还扩张了区间范围)
2.HardTanh
HardTanh函数,是深度学习应用中使用的Tanh激活函数的另一个变体。HardTanh代表了Tanh的一个更便宜、计算效率更高的版本。Hardtanh函数已经成功地应用于自然语言处理中,作者报告说,它在速度和准确率上都有所提高。
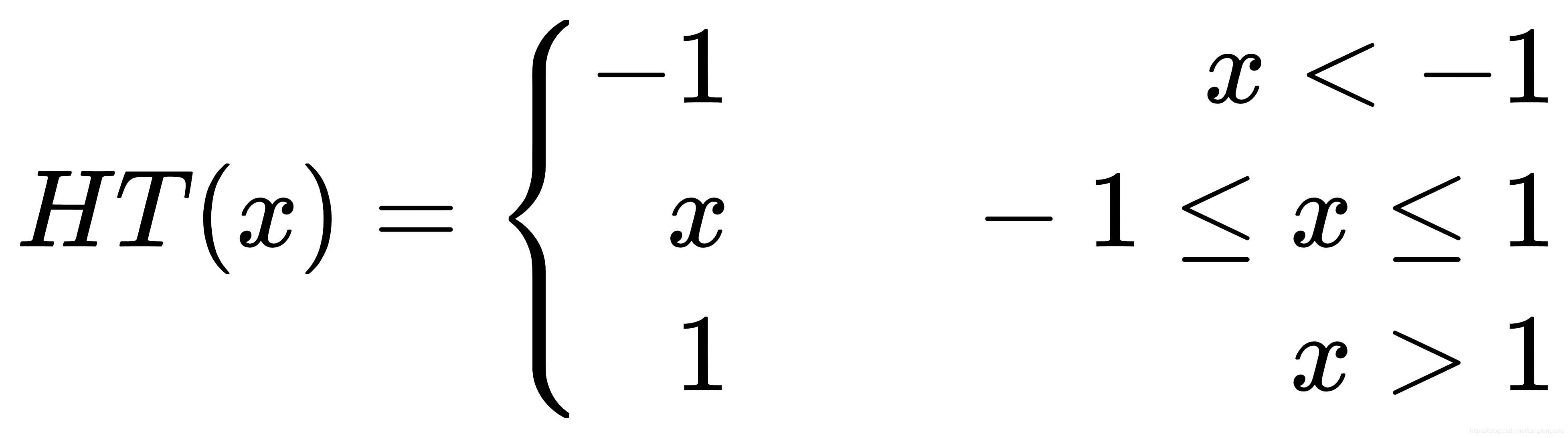

ReLu类
1.ReLU
ReLu函数,Rectified Linear Unit,又称 修正线性单元
R
e
L
u
(
x
)
=
m
a
x
(
0
,
x
)
ReLu(x)=max(0,x)
ReLu(x)=max(0,x)

ReLu设计已成为了深度网络的标配,当下深度网络的结构和relu相关的两大标配:He初始化(对ReLu网络有利)和Conv->BN->ReLu(默认采用relu)
改进:
彻底消灭了正半轴上的死区;计算超简单;正是因为Alex Net中提出了ReLu,在当时很好地缓解了梯度弥散,使得网络深度的天花板第一次被打破;该设计有助于使模型参数稀疏。
缺点
期望均值跑得离0更远了;负半轴上的死区直接蚕食到了 0点
2.ReLu6
由于Relu函数的正半轴不施加任何非线性约束,因此当输入为正大数时,易引起正半轴上的梯度爆炸。因此,Relu6 应运而生
R
e
L
u
6
(
x
)
=
m
i
n
(
m
a
x
(
0
,
x
)
,
6
)
ReLu6(x)=min(max(0,x),6)
ReLu6(x)=min(max(0,x),6)

改进:
对正半轴 施加了 非线性约束;计算超简单
缺点:
期望均值依然不为 0 ;正半轴上的“死区”死灰复燃,从ReLu的 ( − ∞ , 0 ) (-\infty,0) (−∞,0)蚕食至 ReLu6的 ( − ∞ , 0 ) ⋃ ( 6 , ∞ ) (-\infty,0)\bigcup(6,\infty) (−∞,0)⋃(6,∞),但是15年BN出来之后,输入被归一化到了 ( − 1 , 1 ) (-1,1) (−1,1)之间。因此,ReLu6的设计就显得没有必要了
3.Leaky ReLu
对ReLu函数新增一超参数
a
a
a,以解决负半轴的“死区”问题
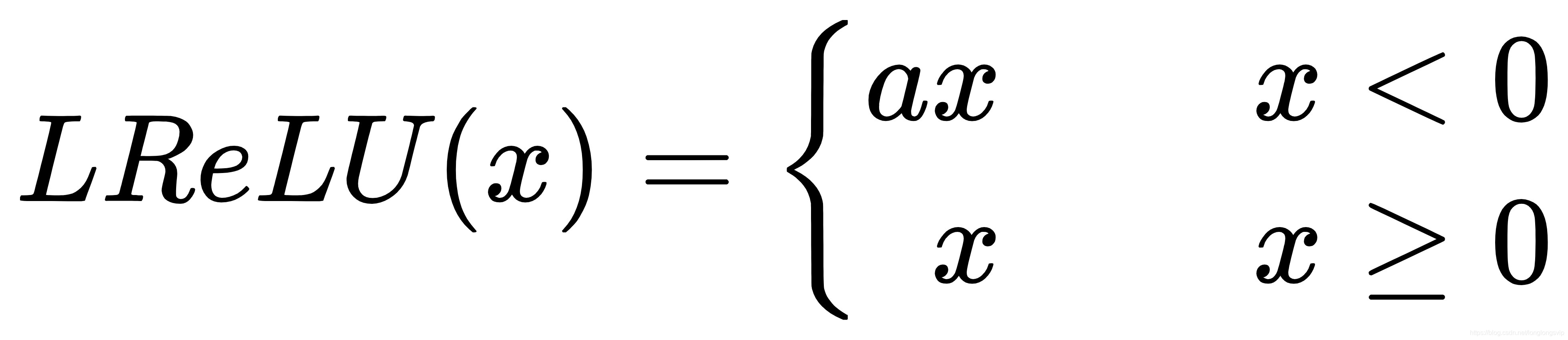
其中,超参数常
a
a
a被设定为0.01或0.001数量级的较小正数
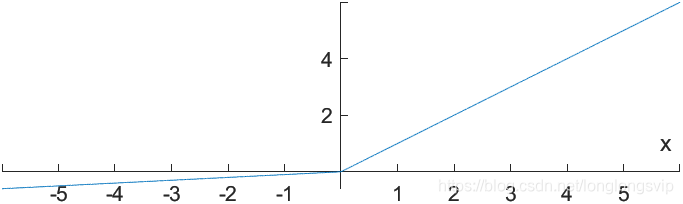
改进:
把 负半轴上的“死区”也端了,从此再无“死区”
缺点:
期望均值依然不为0;合适的 λ \lambda λ值较难设定且较为敏感,导致在实际使用中性能不稳定
4.参数化ReLu
将Leaky ReLu函数中的超参数 a a a设置为和模型一起被训练到的变量,以解决 a a a值较难设定的问题
改进:
更大自由度
缺点:
更大的过拟合风险;较为麻烦
随机化ReLu
将 Leaky ReLu函数中的超参数 a a a随机设置
5.ELU
ELU函数,Exponential Linear Unit,又称指数化线性单元 ,于2016年提出
E
L
U
(
x
)
=
{
x
,
x
≥
0
a
(
e
x
−
1
)
,
x
<
0
ELU(x)=\left\{ \begin{aligned} x,& &x\ge0\\ a(e^x-1),& &x<0 \\ \end{aligned} \right.
ELU(x)={x,a(ex−1),x≥0x<0

其中,超参数
a
a
a常备设定为1
改进:
完美解决了“死区”问题
缺点:
期望均值依然不为0;计算较为复杂
























 2632
2632

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








