机器学习实战笔记5(logistic回归)

1：简单概念描述

假设现在有一些数据点，我们用一条直线对这些点进行拟合(该线称为最佳拟合直线)，这个拟合过程就称为回归。训练分类器就是为了寻找最佳拟合参数，使用的是最优化算法。

这就是简单的线性回归问题，可以通过最小二乘法求解其参数，最小二乘法和最大似然估计见：http://blog.csdn.net/lu597203933/article/details/45032607。 但是当有一类情况如判断邮件是否为垃圾邮件或者判断患者癌细胞为恶性的还是良性的，这就属于分类问题了，是线性回归所无法解决的。这里以线性回归为基础，讲解logistic回归用于解决此类分类问题。

基于sigmoid函数分类：logistic回归想要的函数能够接受所有的输入然后预测出类别。这个函数就是sigmoid函数，它也像一个阶跃函数。其公式如下：

其中： z = w₀x₀+w₁x₁+….+w_nx_n,w为参数， x为特征

为了实现logistic回归分类器，我们可以在每个特征上乘以一个回归系数，然后把所有的结果值相加，将这个总和结果代入sigmoid函数中，进而得到一个范围在0~1之间的数值。任何大于0.5的数据被分入1类，小于0.5的数据被归入0类。所以，logistic回归也可以被看成是一种概率估计。

亦即公式表示为：

g(z)曲线为：

此时就可以对标签y进行分类了：

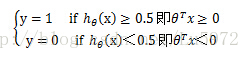
其中θ^Tx=0 即θ0+θ1*x1+θ2*x2=0 称为决策边界即boundarydecision。

Cost function:

线性回归的cost function依据最小二乘法是最小化观察值和估计值的差平方和。即：

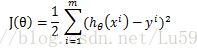
但是对于logistic回归，我们的cost fucntion不能最小化观察值和估计值的差平法和，因为这样我们会发现J(θ)为非凸函数，此时就存在很多局部极值点，就无法用梯度迭代得到最终的参数(来源于AndrewNg video)。因此我们这里重新定义一种cost function

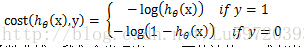
通过以上两个函数的函数曲线，我们会发现当y=1，而估计值h=1或者当y=0，而估计值h=0,即预测准确了，此时的cost就为0，，但是当预测错误了cost就会无穷大，很明显满足cost function的定义。

可以将上面的分组函数写在一起：