图像变换中的常用插值方法（含公式推导）

最新推荐文章于 2024-01-17 10:54:03 发布

3TV

最新推荐文章于 2024-01-17 10:54:03 发布

阅读量4.7k

点赞数 4

分类专栏：图像

本文链接：https://blog.csdn.net/lyx_323/article/details/88219738

版权

图像专栏收录该内容

13 篇文章 2 订阅

订阅专栏

在图像的基本仿射变换（图形变换）中，经常会碰到经过旋转、缩放后灰度值如何赋值的问题。因为变换之后，图像的坐标位置有可能是小数，而图像是以离散的方式表示的，所以就需要插值算法来确定到底将该像素赋予哪个具体的整数值位置上。

1、最邻近插值法(Nearest Interpolation)

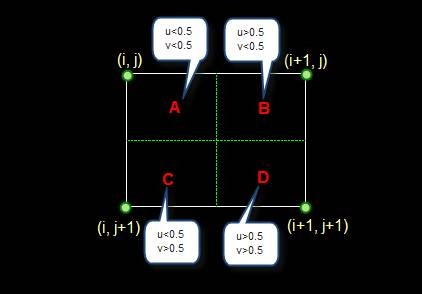
这是最简单的一种插值方法，不需要计算。在待求像素的四邻像素中，将距离待求像素最近的邻接像素灰度值赋予待求像素。设i+u, j+v(i, j为正整数， u, v为大于零小于1的小数，下同)为待求象素坐标，则待求象素灰度的值 f(i+u, j+v) 如下图所示：

如果(i+u, j+v)落在A区，即u<0.5, v<0.5，则将左上角象素的灰度值赋给待求象素，同理，落在B区则赋予右上角的象素灰度值，落在C区则赋予左下角象素的灰度值，落在D区则赋予右下角象素的灰度值。

最邻近元法计算量较小，但可能会造成插值生成的图像灰度上的不连续，在灰度变化的地方可能出现明显的锯齿状。

2、双线性内插法(Bilinear Interpolation)

双线性插值，又称为双线性内插。在数学上，双线性插值是有两个变量的插值函数的线性插值扩展，其核心思想是在两个方向分别进行一次线性插值。

假如我们想得到未知函数 f 在点 P=(x,y) 的值，假设我们已知函数 f 在 $Q_{11} = \left( x_1, y_1 \right)$ , $Q_{12} = \left( x_1, y_2 \right)$ , $Q_{21} = \left( x_2, y_1 \right)$ 及 $Q_{22} = \left( x_2, y_2 \right)$ 四个点的值。

首先在 x 方向进行线性插值，得到

$f(R_1) \approx \frac{x_2-x}{x_2-x_1} f(Q_{11}) + \frac{x-x_1}{x_2-x_1} f(Q_{21}) \quad\mbox{Where}\quad R_1 = (x,y_1),$

$f(R_2) \approx \frac{x_2-x}{x_2-x_1} f(Q_{12}) + \frac{x-x_1}{x_2-x_1} f(Q_{22}) \quad\mbox{Where}\quad R_2 = (x,y_2).$

然后在 y 方向进行线性插值，得到

这样就得到所要的结果 $f \left( x, y \right)$

$f(x,y) \approx \frac{f(Q_{11})}{(x_2-x_1)(y_2-y_1)} (x_2-x)(y_2-y) + \frac{f(Q_{21})}{(x_2-x_1)(y_2-y_1)} (x-x_1)(y_2-y)$

$+ \frac{f(Q_{12})}{(x_2-x_1)(y_2-y_1)} (x_2-x)(y-y_1) + \frac{f(Q_{22})}{(x_2-x_1)(y_2-y_1)} (x-x_1)(y-y_1).$

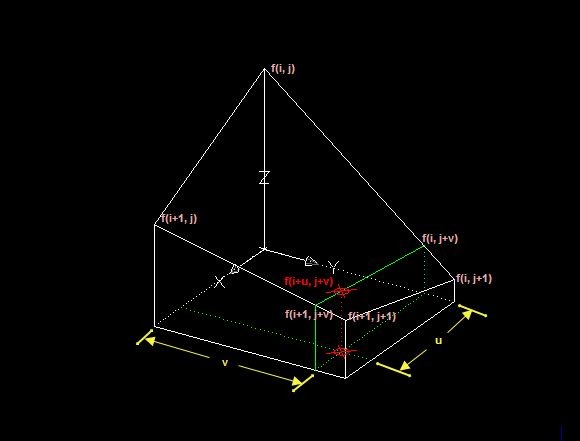
双线性内插法是利用待求像素四个邻像素的灰度在两个方向上作线性内插，如下图所示：u和v位于（0，1）之间

我们先在y上面插值，求f(i, j+v)，(i+1, j+v)，再在x上插值，求像素 f(i+u, j+v)。

现在已知像素是 f(i, j)，f(i, j+1)，f(i+1, j)，f(i+1, j+1)。

y上插值：

对于中间待求 f(i, j+v)，f(i, j) 到 f(i, j+1) 的灰度变化为线性关系，则有：

x： i不变，y：j -> j+v -> j+1： f(i, j+v) = [f(i, j+1) - f(i, j)] * v + f(i, j)

$f\left ( i, j+v \right )= \frac{\left ( j+1 \right )-\left ( j+v \right )}{ j+1 - j }f\left ( i, j \right )+\frac{ j+v - j }{j+1 - j }f\left ( i, j+1 \right )$

$= \left ( 1-v \right )f\left ( i, j \right )+vf\left ( i,j+1 \right )$

$=\left [ f\left ( i, j+1 \right ) - f\left ( i, j \right )\right ] * v + f\left ( i, j \right )$

同理对于 f(i+1, j+v) 则有：

x： i+1不变，y：j -> j+v -> j+1： f(i+1, j+v) = [f(i+1, j+1) - f(i+1, j)] * v + f(i+1, j)

$f\left ( i+1, j+v \right )= \frac{\left ( j+1 \right )-\left ( j+v \right )}{ j+1 - j }f\left ( i+1, j \right )+\frac{ j+v - j }{j+1 - j }f\left ( i+1, j+1 \right )$

$= \left ( 1-v \right )f\left ( i+1, j \right )+vf\left ( i+1, j+1 \right )$

$=\left [ f\left ( i+1, j+1 \right ) - f\left ( i+1, j \right )\right ] * v + f\left ( i+1, j \right )$

x上插值：

从f(i, j+v) 到 f(i+1, j+v) 的灰度变化也为线性关系，由此可推导出待求象素灰度的计算式如下：

y： j+v不变，x：i -> i+u -> i+1： f(i+u, j+v) = [f(i+1, j+v) - f(i, j+v)] * u + f(i, j+v)

= (1-u) * (1-v) * f(i, j) + (1-u) * v * f(i, j+1) + u * (1-v) * f(i+1, j) + u * v * f(i+1, j+1)

$f\left ( i+u, j+v \right )= \frac{\left ( i+1 \right )-\left ( i+u \right )}{ i+1 - i }f\left ( i, j+v \right )+\frac{ i+u - i }{i+1 - i }f\left ( i+1, j+v \right )$

$= \left ( 1-u \right )f\left ( i, j+v \right )+uf\left ( i+1, j+v \right )$

这里，f(i, j+v)以及f(i+1, j+v)已经在前面求解出来，直接带入化解就好。

双线性内插法的计算比最邻近点法复杂，计算量较大，但没有灰度不连续的缺点。它具有低通滤波性质，使高频分量受损，图像轮廓可能会有一点模糊，图像看起来更光滑。

opencv和Matlab中的双线性插值

这部分的前提是，你已经明白什么是双线性插值并且在给定源图像和目标图像尺寸的情况下，可以用笔计算出目标图像某个像素点的值。当然，最好的情况是你已经用某种语言实现了网上一大堆博客上原创或转载的双线性插值算法，然后发现计算出来的结果和matlab、openCV对应的resize（）函数得到的结果完全不一样。

那这个究竟是怎么回事呢？

其实答案很简单，就是坐标系的选择问题，或者说源图像和目标图像之间的对应问题。

假设源图像大小为mxn，目标图像为axb。那么两幅图像的边长比分别为：m/a和n/b。注意，通常这个比例不是整数，编程存储的时候要用浮点型。目标图像的第（i,j）个像素点（i行j列）可以通过边长比对应回源图像。其对应坐标为（i*m/a,j*n/b。按照网上一些博客上写的，源图像和目标图像的原点（0，0）均选择左上角，然后根据插值公式计算目标图像每点像素，假设你需要将一幅5x5的图像缩小成3x3，那么源图像和目标图像各个像素之间的对应关系如下：

只画了一行，用做示意，从图中可以很明显的看到，如果选择左上角为原点（0，0），那么最右边和最下边的像素实际上并没有参与计算，而且目标图像的每个像素点计算出的灰度值也相对于源图像偏左偏上。

那么，让坐标加1或者选择右下角为原点怎么样呢？很不幸，还是一样的效果，不过这次得到的图像将偏右偏下。

最好的方法就是，两个图像的几何中心重合，并且目标图像的每个像素之间都是等间隔的，并且都和两边有一定的边距，这也是matlab和openCV的做法。如下图：

在计算对应坐标的时候改为以下公式即可，

int x=(i+0.5)*m/a-0.5

int y=(j+0.5)*n/b-0.5

代替

int x=i*m/a

int y=j*n/b

利用上述公式，将得到正确的双线性插值结果

文中的内容参考了一些前辈们的博文，现列之如下：

https://blog.csdn.net/xjz18298268521/article/details/51220576

http://www.cnblogs.com/funny-world/p/3162003.html

https://blog.csdn.net/zyttae/article/details/42710303

3TV

关注

4
点赞
踩
15

收藏

觉得还不错? 一键收藏
0
评论
图像变换中的常用插值方法（含公式推导）

在图像的基本仿射变换（图形变换）中，经常会碰到经过旋转、缩放后灰度值如何赋值的问题。因为变换之后，图像的坐标位置有可能是小数，而图像是以离散的方式表示的，所以就需要插值算法来确定到底将该像素赋予哪个具体的整数值位置上。1、最邻近插值法(Nearest Interpolation)这是最简单的一种插值方法，不需要计算。在待求像素的四邻像素中，将距离待求像素最近的邻接像素灰度值赋予待求像素。设...
复制链接

扫一扫