科研论文 | 影响关系研究44种回归模型汇总，SPSSAU软件全部轻松完成

spssau

于 2025-02-28 08:30:00 发布

阅读量2k

点赞数 43

文章标签：回归 SPSSAU 统计学机器学习数据分析论文

本文链接：https://blog.csdn.net/m0_37228052/article/details/145873967

版权

本文介绍了实证分析44种回归模型及其适用场景，重点总结了应该如何选择常用的回归模型，包括多元线性回归、逐步回归、岭回归、logistic回归等，以及介绍如何利用SPSSAU这一软件轻松完成回归分析。

一、40+回归模型汇总

通过回归模型，我们可以深入分析自变量X与因变量Y之间的关系，回归分析可以揭示自变量X对Y的整体影响，还能细致地评估每个自变量X对Y的具体影响程度，从而为决策提供更准确的依据。

目前在SPSSAU系统中，回归模型包含以下40多种，一句话描述及说明如下：

那么面对如此多的回归模型，第一次进行实证分析研究影响关系的同学们应该如何选择呢？

二、回归模型选择

实证分析影响关系研究时，回归模型的选择通常需要结合自变量X和因变量Y的数据类型以及个数进行确定，虽然上文列出了40多种回归模型，但其实日常研究中最常用的回归模型其实就那么几个，接下来以常用回归模型选择为例进行说明。
科研论文常用回归模型初步选择方法如下：

1、Y为定量数据（仅1个）

多元线性回归

当因变量Y为定量数据且只有1个时，一般多元线性回归比较常用。多元线性回归是当前使用最为成熟，研究最多的回归分析方法之一。

线性回归模型有很多需要满足的前提条件（如线性、独立性、正态性、方差齐、无多重共线性），如果不满足这些假定或者条件可能会导致模型使用出错，那么此时就有对应的其它回归模型出来解决这些问题，因而跟着线性回归后面又出来很多其他回归分析方法。

关于多元线性回归模型可查看下方文章：

深度解析 | 多元线性回归模型（超详细适用条件检验、软件操作及结果解读）

逐步回归

分析X对Y的影响关系时，X可以为多个，但并非所有X均会对Y产生影响；当X个数很多时,可以让系统自动识别出有影响的X，这一自动识别分析方法则称为逐步回归分析，具体可分为逐步法、向前法、向后法。

岭回归

岭回归是一种正则化的线性回归方法，特别适用于处理多重共线性问题。它通过在损失函数中添加一个L2惩罚项（即回归系数的平方和乘以一个常数）来减少共线性对参数估计的影响，从而提高模型的稳定性，但可能会牺牲一些模型的解释力。

lasso回归

岭回归是使用L2正则化，Lasso回归是使用L1正则化。相对来讲，岭回归用于解决共线性问题的时候较多，Lasso回归除了有解决共线性问题的功能外，其还可用于进行‘特征筛选’，即找出有意义的自变量X，一般在机器学习领域使用此功能较多。

Robust回归

是一种对异常值和模型误设定不那么敏感的回归方法。它使用不同的损失函数来减少异常值对回归系数估计的影响，使得模型更加健壮，适用于数据中存在较多异常值的情况。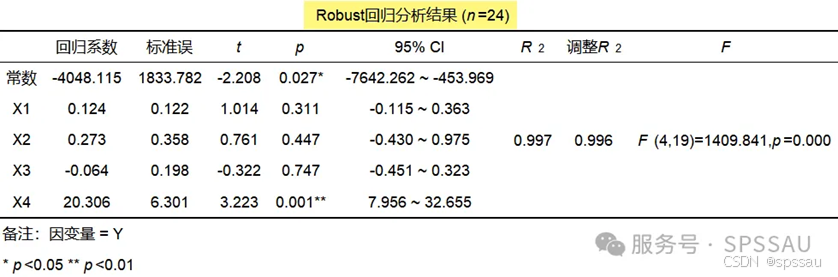

分层回归/分组回归

分层回归用于处理数据存在层次结构的情况，考虑不同层次的效应。分组回归则是根据某些特征将数据分组，并在每组中进行回归分析。

曲线回归/非线性回归

曲线回归或非线性回归用于建模因变量和自变量之间的非线性关系。这种方法通过使用多项式函数、指数函数、对数函数等非线性函数来更好地拟合数据，从而提供更准确的预测和解释。

面板模型

用于分析时间序列数据和横截面数据的组合，考虑时间和个体效应。适用于研究变量随时间变化的影响。

2、Y为定量数据（多个）

一般回归模型只包括一个因变量Y，如果研究存在多个因变量Y，可以根据研究选择PLS回归、路径分析或者结构方程模型。

PLS回归

PLS回归（偏最小二乘回归），是一种可以解决共线性问题、多个因变量Y同时分析、以及处理小样本时影响关系研究的一种多元统计方法。从原理上，PLS回归集合三种研究方法，分别是多元线性回归、典型相关分析和主成分分析，PLS回归是此三种方法的集合运用，多元线性回归用于研究影响关系，典型相关分析用于研究多个X和多个Y之间的关系，主成分分析用于对多个X或者多个Y进行信息浓缩。

路径分析

路径分析在于研究模型影响关系，用于对模型假设进行验证。

结构方程模型（SEM）

可用于研究多个潜变量之间的影响关系情况。结构方程模型共包括两部分结构，分别是测量关系和影响关系。

3、Y为定类数据

当因变量Y为定类数据时，logistic回归模型比较常用。

二元logistic回归

因变量为二分类变量时，比如“买&不买”、“阳性&阴性”，选择二元logistic回归分析。还有两种方法，二元probit回归、条件logistic回归，也可针对二分类变量进行回归分析。

多分类logistic回归

因变量为多分类变量时，比如村长候选人“甲、乙、丙”，选择多分类logistic回归分析。

有序logistic回归

因变量为多分类变量且有序时，比如“不满意、一般、满意”，选择有序logistic回归分析。
上面提到的这些方法都是在实际科学研究、论文实证分析中使用频率非常高的回归模型，可以满足绝大多数分析使用。

三、其他应用场景分类

上文已经对Y为定量数据、Y为定类数据时一些常用的模型进行了说明。下面对其余的三类应用场景——问卷研究、医学研究、空间计量研究常用回归模型进行介绍。

1、问卷研究

通过量表问卷收集的数据，常用的回归模型有调节作用、中介作用、调节中介、路径分析、结构方程模型，它们不是严格意义上的回归模型，但是本质也是研究影响关系的模型。

调节作用

调节作用是研究X对Y的影响时，是否会受到调节变量Z的干扰；比如开车速度（X）会对车祸可能性（Y）产生影响，这种影响关系受到是否喝酒（Z）的干扰，即喝酒时的影响幅度，与不喝酒时的影响幅度是否有着明显的不一样。

中介作用

中介作用是研究X对Y的影响时，是否会先通过中介变量M，再去影响Y；即是否有X->M->Y这样的关系；比如工作满意度（X）会影响到创新氛围（M）,再影响最终工作绩效（Y）。

调节中介

调节中介作用同时考虑中介变量和调节作用，其核心是中介作用，基于中介作用基础上再进一步讨论调节作用。比如X->M->Y这条中介路径存在，即说明具有中介作用。接着在进一步分析条件中介作用，即在另外一个调节变量Z取不同水平时（通常分为3个水平，低水平，平均水平，高水平），中介作用的幅度（也称条件间接效应）情况如何。