学习笔记,仅供参考,有错必纠
时间序列
DF统计量和t统计量的分布特征
情形1

- t ( β ^ ) t(\hat{\beta}) t(β^)的极限分布和有限样本分布特征



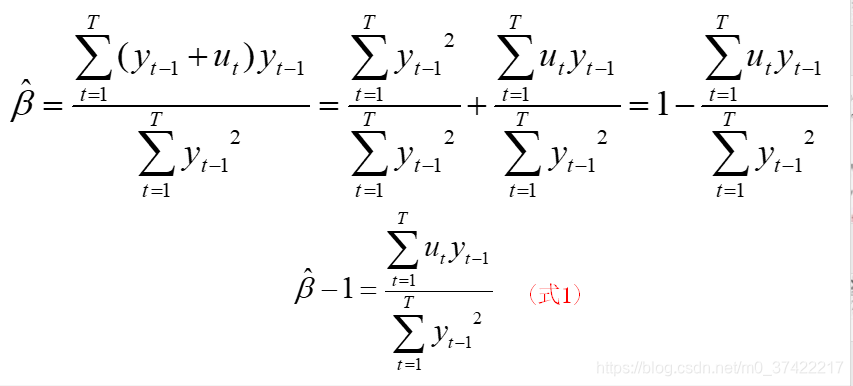

由式(1)、式(2)、式(3)可知,当 T → ∞ T \to \infty T→∞时:

T ( β ^ − 1 ) T(\hat{\beta}-1) T(β^−1)是检验单位根的一个常用统计量。有三个结论如下:

检验单位根的另一个统计量是 t ( β ^ ) t_{(\hat{\beta})} t(β^)统计量。 t ( β ^ ) t_{(\hat{\beta})} t(β^)统计量在这里称 DF 统计量。当 T → ∞ T \to \infty T→∞时:

有限样本条件下的 DF 统计量的分布特征(蒙特卡罗模拟结果):

T=100,模拟1万次的DF统计量的分布结果:

情形2
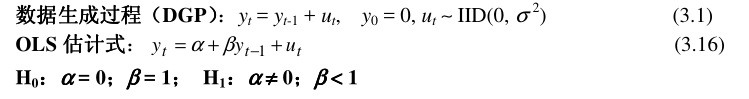
- t ( β ^ ) , t ( α ^ ) t(\hat{\beta}), t(\hat{\alpha}) t(β^),t(α^)的极限分布和有限样本分布特征


有限样本条件下的 DF 统计量的分布特征(蒙特卡罗模拟结果):
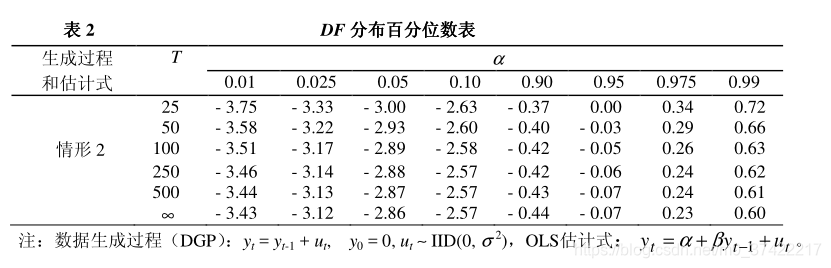
T=100,模拟1万次的DF统计量的分布结果:

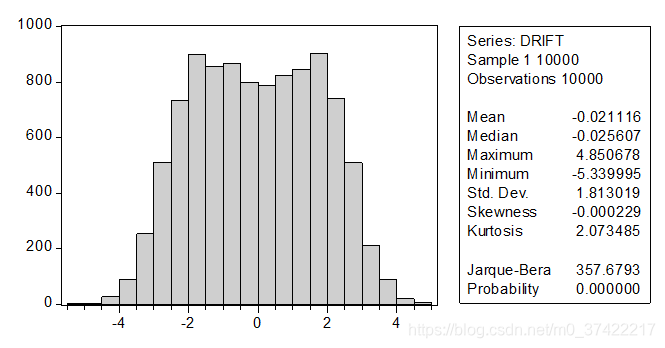
有限样本条件下的 t ( α ^ ) t(\hat{\alpha}) t(α^)统计量的分布特征(蒙特卡罗模拟结果):

T = 100 条件下, t ( α ^ ) t(\hat{\alpha}) t(α^) 的分布见图:

情形3

- D F = t ( β ^ ) , t ( α ^ ) , t ( γ ^ ) DF=t(\hat{\beta}), t(\hat{\alpha}), t(\hat{\gamma}) DF=t(β^),t(α^),t(γ^)的极限分布和有限样本分布特征


有限样本条件下的DF统计量的分布特征(蒙特卡罗模拟结果):

T=100,模拟1万次的DF统计量的分布结果:

有限样本条件下的 t ( α ^ ) t(\hat{\alpha}) t(α^)统计量的分布特征(蒙特卡罗模拟结果):

T = 100 条件下, t ( α ^ ) t(\hat{\alpha}) t(α^) 的分布见图:
有限样本条件下的 t ( γ ^ ) t(\hat{\gamma}) t(γ^)统计量的分布特征(蒙特卡罗模拟结果):

T = 100 条件下, t ( γ ^ ) t(\hat{\gamma}) t(γ^) 的分布见图:

D F = t ( β ^ ) DF=t(\hat{\beta}) DF=t(β^), t ( α ^ ) t(\hat{\alpha}) t(α^)与 t ( γ ^ ) t(\hat{\gamma}) t(γ^)的比较:


























 1399
1399

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?










