模糊PID算法及其MATLAB仿真（2）

天狭鬼

已于 2022-03-04 21:02:18 修改

阅读量8.9w

收藏 1.5k

点赞数 194

分类专栏： learn 文章标签： Matlab PID Fuzzy

于 2019-04-16 18:05:07 首次发布

本文链接：https://blog.csdn.net/m0_37763336/article/details/89325795

版权

learn 专栏收录该内容

20 篇文章

订阅专栏

上一篇写了模糊自整定PID的理论，这篇来做MATLAB仿真。

补充内容：如何计算临界稳定下的开环增益 Ku 和震荡周期 Tu

MATLAB进行模糊PID仿真

1、准备工作

2、模糊控制器的设计

前置说明：由于本人长期在外地出差，还没有时间来做本文中模型的Debug, 也未对每一步深入研究。请各位先参考评论区自行检查，我后续会更新本文。十分抱歉。

补充内容：如何计算临界稳定下的开环增益 Ku 和震荡周期 Tu

学过控制工程或者相关理论的同学应该比较了解，判断系统稳定性的条件一般用到劳斯表（劳斯判据）。而PID控制和模糊PID控制极大地依赖系统传递函数的建立，因此如果对于系统复杂，难以建立模型的，还是需要考虑一下。

（1）通过自己对所需要控制的系统进行建模，拉普拉斯变换得到传递函数Gc(s)，然后求得其特征方程（形式如下）：

其闭环系统特征方程可以表示为：

特征方程的计算就是要求闭环系统传递函数的分母为0，如果是开环系统，就将传递函数的分子和分母加起来作为特征方程。

（2）将系统特征方程中的s用（-jw）代替，然后令实部和虚部分别等于0，解出特征根。特征根 w 就是震荡频率,K 为开环增益。

则，周期 Td = 2PI/w 。这样就可以用来求取PID参数的论域了。

以上下划线理论有问题，验证后发现并不是这样计算。

修改内容：

修改PID三个参数的模糊论域为

P = [0 0.1];

I = [0.0.05];

D = [0.0.1];

MATLAB进行模糊PID仿真

1、准备工作

首先需要选取传递函数，设系统传递函数方程如下：

纯属为了计算方便。解得 K=8，w^2=3。

先看使用 Simulink 自带的仿真结果，其PID参数整定的情况：

接下来设计模糊自整定PID。

2、模糊控制器的设计

步骤：

（1）打开 MATLAB ，选择一个工作目录，这里一般选择一个可写的磁盘即可。为什么要可写的呢，因为C盘有些目录下你的用户权限是不可写的，所以就算你设计的没有问题也没法运行。

（2）命令行输入fuzzy，打开模糊规则编辑器。

（3）Edit -> Add variables -> Input；Edit -> Add variables -> Output；Edit -> Add variables -> Output。单击选中，分别对 input1 、input2、output1、output2、output3 进行隶属度编辑。对于输入进行命名，分别为误差 E 和误差变化率 EC。输出分别命名为P、I、D，其他不变。

（4）双击 Input1 进入隶属度编辑器，Edit -> Add MFS 。添加隶属度函数，这里采用三角形隶属度函数，添加4个，实际应该对每一个都添加4个，并进行编辑。

（5）其中 E 和 EC 的论域（Range）取 [-6 6]，然后对每个隶属度曲线进行编辑。这里有两个小问题（或者说是小技巧）。

a. 论域的划分，抛开模糊PID理论来说，其实论域的划分很大程度上取决于个人的方法，灵活性很大。你可以认为身高180的人很高、也可以认为较高，甚至可以认为较矮，只是隶属度不同。这些都取决于你的系统，但是常规是均匀划分的，例如这篇博客。然后我自己想了一种方法（适用于7隶属度）：半区间宽度=（论域总长度/12）*2，也就是说一个大三角由两个半区间组成。

b. 还有就是隶属度函数命名的时候，最好是有顺序的，单击隶属度函数曲线，设计顺序：mf1->NL;mf2->NM;mf3->NS;mf4->ZE;mf5->PS;mf6->PM;mf7->PL。这样设置的好处是后面添加模糊规则的时候很方便。

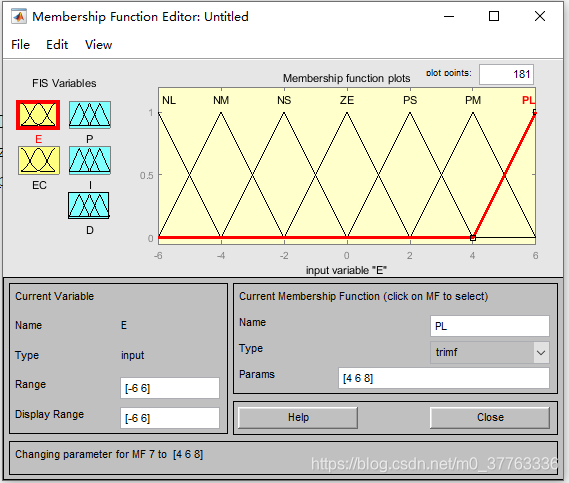
（6）设计PID三个参数的输出隶属度

按照上一篇的介绍，三个参数的隶属度选择范围如下，近似的话建议扩大论域区间：

Kp = [0.32Ku 0.6Ku] = [2.56 4.80] $\approx$ [2,5]

Ki = [0.32Tu 0.47Tu] = [1.1608 1.7050] $\approx$ [1 2] // 这里用[1 2]可能存在结果1的情况，结果2用的[1 3]

Kd = [2Tu 5Tu] = [7.2552 18.1380] $\approx$ [7 19]

按照之前的方法进行划分，获得隶属度函数分布区间：

Kp 的论域划分

隶属度	NL	NM	NS	ZE	PS	PM	PL
区间	[1.5 2 2.5]	[2 2.5 3]	[2.5 3 3.5]	[3 3.5 4]	[3.5 4 4.5]	[4 4.5 5]	[4.5 5 5.5]

Ki 的论域划分

隶属度	NL	NM	NS	ZE	PS	PM	PL
区间	[0.833 1 1.167]	[1 1.167 1.333]	[1.167 1.333 1.5]	[1.333 1.5 1.667]	[1.5 1.667 1.833]	[1.667 1.833 2]	[1.833 2 2.167]

Kd 的论域划分

隶属度	NL	NM	NS	ZE	PS	PM	PL
区间	[5 7 9]	[7 9 11]	[9 11 13]	[11 13 15]	[13 15 17]	[15 17 19]	[17 19 21]

直接复制上去吧！！！！

其实这里还有很多不严谨的地方，比如隶属度论域的计算方法。

（7）设计模糊规则，这里的设计规则选取的是一篇文献中的规则表，我主要是考虑方便，实际上，这种模糊规则表是决定模糊PID效果的关键之一（还有就是隶属度函数的确定）。如果这里设计的不好，最后出来的PID阶跃响应可能还不如手工调整PID，虽然这种方式对于在线调整是不太可能实现的。调整规则如下，参考文献 [2]。

双击下图圈中方框：

调整规则：

第一个隶属度图中的圈内换成PL，第二个图换成ZE（其实这里不确定，我换的ZE）。

根据隶属度规则表挨个添加进 Rule Editor 即可

（8）导入工作空间

关闭规则编辑器。单击 file-> export -> To file... 命名为Fuzzy_PID.fis -> 保存。

单击 File -> Export -> To workspace -> OK。

我们会发现在MATLLAB的工作区（Workspace）有来了一个1*1 struct的值。

（9）Simulink中进行仿真。

在命令行里输入simulink，或者在MATLAB主页点击Simulink，打开Simulink工具箱。新建一个空白Blank。

在库里面找到Fuzzy Logic Controlller模块，拖到Blank里面。相关的还需要step（阶跃信号），sum（输入输出反馈），PID（一个完整的控制算法块，也可以自己写），mux（用于整合图形），scope（显示结果）。

（10）然后一步一步设置：

双击sum，将sum的配置改为下图：

双击PID Controller，使source为external，也就是PID接收外部参数。

PID改完之后是这样的：

双击传递函数(Transfer Fun)，修改如下：

如果显示 num(s)/den(s) 的形式，可以把它放大，和你放大窗口是一样的。

设置Fuzzy controller，同样双击。

这个名字要和你工作空间的一样才行，有些同学虽然改了，但是还是不成功，可能就是你没能导入到工作空间里面。自寻解决办法（readfis()函数）。

以下为错误

结果1：

结果2：Ki 的区间从[1,2] 修改为[1,3].

目前结果是这样，我再调一调看看。

不妥之处恳请广大朋友指出。

增加：评论区有位指出积分时间常数和PID系数Ki的问题，这里贴个PID的方程：

典型PID控制器的传递函数为：

$G_{c}(s)=K_{p}(1+\frac{1}{T_{i}s}+T_{d}s)$

而离散PID控制方程可以表示为：

$U(n)=K_{p}[e(n)+\frac{T}{T_{i}}\sum e(i)+\frac{T_{d}}{T}(e(n)-e(n-1)))]$

源程序！源程序！GitHub - NidhoghostX/Fuzzy-PID-on-Matlab

CSDN 要收费下载，资源转到Github了。

——————————————————————————————————————————————

更新：

二维模糊PID的matlab仿真（官网教程）：Fuzzy PID Control with Type-2 FIS- MATLAB & Simulink

现在在忙，没有时间研究，今后可能会做一下。

参考文献

[1] https://sci-hub.tw/10.1115/1.2899060 （最早经典的PID参数整定文章，大部分文献都会用到）

[2] S. krishna, S. Vasu,Fuzzy PID based adaptive control on industrial robot system,Materials Today: Proceedings,Volume 5, Issue 5, Part 2,2018,Pages 13055-13060.