摄像机几何成像模型

dotJunz

已于 2022-07-13 20:46:08 修改

阅读量1.7k

点赞数

分类专栏： # 毕设文章标签：计算机视觉

于 2022-03-18 20:09:16 首次发布

原文链接：https://kns.cnki.net/kcms/detail/detail.aspx?dbcode=CMFD&dbname=CMFD202201&filename=1021807951.nh&uniplatform=NZKPT&v=yyhow6HXxWvsWwXGH6X54doXW1t0MLPFpSBpPcd1yqvT0ZOQKXm3nBgeMGHa3D6H

版权

毕设专栏收录该内容

10 篇文章

订阅专栏

本文详细介绍了摄像机几何成像模型，包括世界坐标系、相机坐标系、图像物理坐标系和像素坐标系之间的转换关系。通过刚体变换、透视投影和物理尺寸转换，阐述了如何将三维空间中的点从世界坐标系映射到像素坐标系，涉及到旋转矩阵、平移矩阵以及焦距和像素尺寸等关键参数。

摘要生成于 C知道，由 DeepSeek-R1 满血版支持，前往体验 >

摄像机几何成像模型

摄像机几何成像模型利用数学公式描述了三维空间中一点与二维图像中一点之间的联系。摄像机几何成像模型主要涉及到了四个坐标系，下面将介绍四个坐标系及其之间的转换关系。

四大坐标系

四大坐标系包括世界坐标系、相机坐标系、图像坐标系和像素坐标系，通过建立它们之间的位置关系可以实现二维平面一点与三维空间一点的坐标转换，它们之间的位置关系如图所示。
在这里插入图片描述

四大坐标系的位置关系
世界坐标系 $O_w-X_wY_wZ_w)$ : 世界坐标系是建立在真实世界中的坐标系，它的单位为米(m)，它可以用来描述相机的位置，也可以用来描述三维空间中的所有点。

摄像机坐标系 $O_c-X_cY_cZ_c)$ : 以相机设备的光心 $O_c$ 来建立摄像机坐标的原点位置，其单位为米(m)，横、纵坐标分别与图像坐标系的横、纵坐标轴平行，但是 $Z$ 轴为摄像机的光轴。

图像物理坐标系 $O_l-xy)$ : 图像物理坐标系的原点为图像中心，以毫米(mm)
为单位，横坐标与纵坐标分别平行于摄像机坐标系的横坐标与纵坐标，描述了像素的实际位置。

图像像素坐标系 $O_o-uv)$ : 图像像素坐标系将图像左上角的像素点 $O_c$ 作为原点，它的单位为像素(pixel)，其横纵坐标与图像物理坐标系的横纵坐标分别平行。

坐标系的转换

若已知摄像机的相关参数信息，想将空间内任意一点P从世界坐标系变换到像素坐标系，一共需要经过三次坐标变换，坐标系间的转换关系如图所示。
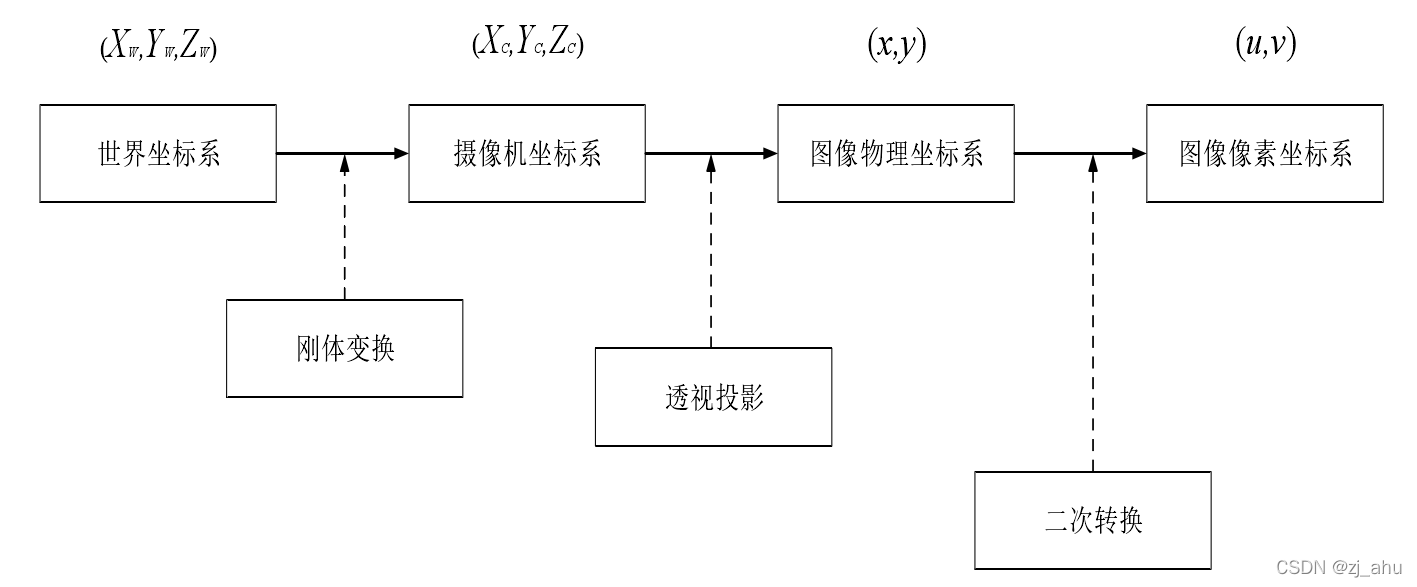
在这里插入图片描述

四大坐标系转换关系示意图

(1)世界坐标系到摄像机坐标系的转换

从世界坐标系转换到摄像机坐标系的过程称为刚体变换，在此变换过程中物体不会出现形变，只需要进行旋转变换和平移变换。为了得到与其相对应的旋转矩阵，可以围绕不同的坐标轴进行不同角度的旋转，则可以得到坐标转换关系如式(1)所示：
$\left[ \begin{matrix} X_c \\ Y_c \\ Z_c \end{matrix} \right] = R\left[ \begin{matrix} X_w \\ Y_w \\ Z_w \end{matrix} \right] + T = \left[ \begin{matrix} r_{11} & r_{12} & r_{13} \\ r_{21} & r_{22} & r_{23} \\ r_{31} & r_{32} & r_{33} \end{matrix} \right]\left[ \begin{matrix} X_w \\ Y_w \\ Z_w \end{matrix} \right] + \left[ \begin{matrix} T_x \\ T_y \\ T_z \end{matrix} \right]\tag{1}$
式中， $X_w,Y_w,Z_w)$ 为在世界坐标系中点P的坐标， $X_c,Y_c,Z_c)$ 为在摄像机坐标系中点P的坐标，R为一共 $3 * 3$ 的矩阵，将它称为旋转矩阵，T为一个 $3 * 1$ 的矩阵，将它称为平移矩阵。将式(1)转换成矩阵形式，如式(2)所示。
$\left[ \begin{matrix} X_c \\ Y_c \\ Z_c \\ 1 \end{matrix} \right] = \left[ \begin{matrix} R & T \\ 0^T & 1 \end{matrix} \right]\left[ \begin{matrix} X_w \\ Y_w \\ Z_w \\ 1 \end{matrix} \right]\tag{2}$

(2)摄像机坐标系到图像物理坐标系的转换

透视投影可以形象地描述摄像机坐标系与图像坐标系之间的转换关系。图像坐标系的原点则是成像平面与摄像机光轴之间的交点，其 $x$ , $y$ 轴与 $X_c$ , $Y_c$ 轴平行。由理想的针孔成像原理可以得到坐标转换关系如式(3)所示。
$\left\{ \begin{aligned} x & = & f \frac {X_c}{Z_c} \\ y & = & f \frac {Y_c}{Z_c} \end{aligned} \right. \tag{3}$

式中， $f$ 为摄像机的焦距，它是一个固定的参数，由摄像机自身决定。将式(3)转换成矩阵形式，如式(4)所示。
$Z_c\left[ \begin{matrix} x \\ y \\ 1 \end{matrix} \right] = \left[ \begin{matrix} f & 0 & 0 & 0 \\ 0 & f & 0 & 0 \\ 0 & 0 & 1 & 0 \end{matrix} \right]\left[ \begin{matrix} X_c \\ Y_c \\ Z_c \\ 1 \end{matrix} \right]\tag{4}$

(3)图像物理坐标系到图像像素坐标系的转换

把投影点 $P$ 进行物理坐标系与像素坐标系间转换的原因是由于二者的单位不同，前者是毫米(mm)，后者是像素(pixel)。假设在像素坐标系下有一个点p，其在x轴和y轴方向上的尺寸为d,和d,，则两个不同的坐标系之间的转换关系如式(5)所示。
$\left\{ \begin{aligned} u & = & \frac {x}{d_x} + u_0 \\ v & = & \frac {y}{d_y} + v_0 \end{aligned} \right. \tag{5}$
式中， $d_x$ , $d_y$ 分别表示在 $x$ 轴和 $y$ 轴方向上的物理尺寸，即每一行和每一列分别表示多少毫米。将式(5)转换成矩阵形式，如式(6)所示。
$\left[ \begin{matrix} u \\ v \\ 1 \end{matrix} \right] = \left[ \begin{matrix} \frac 1{d_x} & 0 & u_0 \\ 0 & \frac 1{d_y} & v_0 \\ 0 & 0 & 1 \end{matrix} \right]\left[ \begin{matrix} x \\ y \\ 1 \end{matrix} \right]\tag{6}$

联立式(6)、式(4)、式(2)，可以将任意一点P从世界坐标系转换到像素坐标系，转换关系如式(7)所示：
$Z_c\left[ \begin{matrix} u \\ v \\ 1 \end{matrix} \right] = \left[ \begin{matrix} \frac 1{d_x} & 0 & u_0 \\ 0 & \frac 1{d_y} & v_0 \\ 0 & 0 & 1 \end{matrix} \right] \left[ \begin{matrix} f & 0 & 0 & 0 \\ 0 & f & 0 & 0 \\ 0 & 0 & 1 & 0 \end{matrix} \right] \left[ \begin{matrix} R & T \\ 0^T & 1 \end{matrix} \right] \left[ \begin{matrix} X_w \\ Y_w \\ Z_w \\ 1 \end{matrix} \right]$
$\left[ \begin{matrix} \frac f{d_x} & 0 & u_0 & 0 \\ 0 & \frac f{d_y} & v_0 & 0 \\ 0 & 0 & 1 & 0 \end{matrix} \right] \left[ \begin{matrix} R & T \\ 0^T & 1 \end{matrix} \right] \left[ \begin{matrix} X_w \\ Y_w \\ Z_w \\ 1 \end{matrix} \right]= M_1M_2\left[ \begin{matrix} X_w \\ Y_w \\ Z_w \\ 1 \end{matrix} \right] \tag{6}$
式中， $f_x=\frac{f}{d_x}$ , $f_y=\frac{f}{d_y}$ 分别为 $u$ 轴和 $v$ 轴方向归一化焦距， $M_1$ 为由摄像机内部结构决定的内部参数矩阵， $M_2$ 为外部参数矩阵，由旋转矩阵 $R$ 和平移矩阵 $T$ 组成。