商汤LoFTR局部特征关键点匹配模型解读（附源码+论文）

LoFTR

论文链接：LoFTR: Detector-Free Local Feature Matching with Transformers

官方链接：LoFTR: Detector-Free Local Feature Matching with Transformers

老规矩，先看一下效果

总体流程

我们先简单过一遍流程，然后在代码里详细说。

首先第一步啊，还是老规矩，用backbone特征提取。不过这里有一点注意，输入的是两张图片A和B，两张图片会拼接在一起然后进行backbone。最后输出一个原图大小1/8的特征图A和B，一个原图大小1/2的特征图A和B。为了方便后续了理解，这里假设1/8的特征图的(h，w)为(60，80)，1/2的特征图的(h，w)为(240，320)。

做完backbone提取的特征图如下。

可以看到，A点和B点的特征非常相似，无论是周边环境还是自己本身的形状都很相似，很容易将A点匹配上B点，所以我们还需要进一步的特征提取。

第二模块就是大名鼎鼎的Transformer，这里分了两块，self-Attention和Cross-Attention。

将刚刚提取的1/8的特征图拿过来，现在我们想对特征图A和特征图B做一个特征点匹配，怎么做呢？挨个询问呗，A里的每个点去问B里的每个点，我跟你匹配得上不？这是不是相当于A里的每个点提供query，B里的每个点提供key和value，这里就是做了一个Cross-Attention。但是有个问题啊，要是A里的好几个点都看上了B的同一个点怎么办？所以咱得先内部商量一下，A内部的每个点都先看看别的点是怎么个事，咱们分个工别选重了，这里就是做了一个self-Attention。这里要注意的点呢，不是做完self再去做cross的，而是先做一个self，再做cross，然在再走self->cross，重复几遍的走。最后得到重构后的特征图A和B。因为Transformer会将二维特征图转为一个序列，所以这时输出的特征图A和B为（B， 4800，dim）。B为批量大小，4800=60×80，dim为特征图维度，比如256。

做完Transformer提取的特征图如下。

这时候我们再看A点和B点，明显就不可能匹配上了。

第三步就要开始做匹配了，不过匹配分两步走，先进行粗粒度匹配，然后再细粒度匹配。

粗粒度匹配会先计算特征图A上的每个点与特征图B上的每个点的一个关系，那就会得到一个[4800,4800]的一个关系矩阵。既然有了关系矩阵，那就可以剔除那些关系不行的匹配点。咱们进行一定的阈值过滤，比如匹配度小于0.2的就扔掉。而且两个点的匹配必须是两两最最好（互近邻），不能是一厢情愿的结果。将这些塑料关系剔除后，将剩余的点进行位置匹配，即找到特征图A上i点对应的特征图B上j点。

咱们为什么说这是一个粗力度匹配呢，你想啊，我们拿来做匹配的特征图都是1/8大小的，这看似是4800个点，其实每个点都包含了原图一块区域的特征，所以我们要再细化一下。

细粒度匹配会将开始backbone提取的1/2的特征图拿过来和粗粒度匹配的结果进行对应。不过这1/2的特征图不是拿点来跟你进行匹配了，而是拿区域跟你进行匹配。通过滑动窗口，可以将图像细分为许多小区域，每个区域由窗口内的特征向量表示。这过程有点像卷积，但跟卷积不同的是它不做任何计算。比如kernel_size=(5,5)，它将这个5×5的区域拿出来展平作为一条数据，然后滑到下一个窗口，拿出这个窗口的数据展平作为一条数据，然后滑到下一个窗口…它也不是一步一步的滑下去，也会进行stride和padding的操作，最后拿到4800条数据，维度为(4800,25,dim)。

巧了这不，你经过粗粒度匹配有4800条数据，我也有，那咱们对应对应呗。假设我们经过粗粒度后有100个区域匹配上了，那么现在咱们手里还剩(100,25,dim)。但是匹配的结果不一定是区域a的中心点与区域b的中心点进行了匹配，可能匹配的是区域a的左上角与区域b的右下角，就是可能会有一些偏移。接下来我们怎么做呢？其实和粗粒度是一样的。粗粒度是4800个点与4800个点做匹配，那细粒度也一以贯之呗，用25个点与25个点进行匹配。但是经过Transform，输入多少dim，输出还是多少dim， 并没有输出一个结果。它只是将特征向量进行了一个重构，但是并不像全连接层输出一个结果啊，所以我们还需要进行一些微调

我们计算5×5区域中，每个点与中心点的一个联系，用softmax计算它们的概率关系，得到一个100×5×5的概率图。 最后我们计算每个区域概率的期望，得到(100,2)的实际位置，这样咱们就匹配上了100个位置。最终完成下图的匹配。

代码

这里直接讲demo怎么跑的，咱们运行demo_loftr.py。

s = VideoStreamer(opt.input, opt.resize, opt.skip, opt.image_glob, opt.max_length)
frame, ret = vs.next_frame()
frame_tensor = frame2tensor(frame, device)
last_data = {'image0': frame_tensor}
...
while True:
    frame, ret = vs.next_frame()
    frame_tensor = frame2tensor(frame, device)
    last_data = {**last_data, 'image1': frame_tensor}
    matcher(last_data)

这里看一下图片导入模型的一个过程。可以看到在初始阶段我们就把第一张图片拿出来了，其作为image0放入last_data中。在下面的while True过程中，每一次会将下一张图片拿出来，作为image1放入last_data中。

直接在loftr.py的forward里打个断点，我们进去看看怎么个事

1、backbone特征提取

loftr.py的forward里分了五步走，我们一一讲解。

首先第一步，提取特征。

# 1. Local Feature CNN
data.update({  # 先提取两张图片
    'bs': data['image0'].size(0),
    'hw0_i': data['image0'].shape[2:], 'hw1_i': data['image1'].shape[2:]
})

if data['hw0_i'] == data['hw1_i']:  # faster & better BN convergence  将两张图片拼接在一起然后传入backbone做特征提取
    feats_c, feats_f = self.backbone(torch.cat([data['image0'], data['image1']], dim=0))  # 输出一个1/8的和一个1/2的特征图
    (feat_c0, feat_c1), (feat_f0, feat_f1) = feats_c.split(data['bs']), feats_f.split(data['bs'])  # 将两张特征图分开
else:  # handle different input shapes
    (feat_c0, feat_f0), (feat_c1, feat_f1) = self.backbone(data['image0']), self.backbone(data['image1'])

data.update({
    'hw0_c': feat_c0.shape[2:], 'hw1_c': feat_c1.shape[2:],
    'hw0_f': feat_f0.shape[2:], 'hw1_f': feat_f1.shape[2:]
})

对应下面的这张图我们来讲解。首先我们拿出这个两张图片，然后将它们拼接在一起放入backbone中。backbone内容我就不说了，就是一些卷积，然后上采样然后再卷积这些操作，得到1/8的特征图feats_c和1/2的特征图feats_f。因为刚刚咱们传进去的时候是拼接在一起的，所以咱再给它分开来，最后得到1/8的特征图(feat_c0, feat_c1)和1/2的特征图(feat_f0, feat_f1)。我们这里假设feat_c0和feat_c1的(b,c,h,w)为(1,256,60,80)。

2、注意力机制

# 2. coarse-level loftr module
# add featmap with positional encoding, then flatten it to sequence [N, HW, C]
feat_c0 = rearrange(self.pos_encoding(feat_c0), 'n c h w -> n (h w) c')  # 给特征图加上位置编码
feat_c1 = rearrange(self.pos_encoding(feat_c1), 'n c h w -> n (h w) c')

mask_c0 = mask_c1 = None  # mask is useful in training
if 'mask0' in data:
    mask_c0, mask_c1 = data['mask0'].flatten(-2), data['mask1'].flatten(-2)
feat_c0, feat_c1 = self.loftr_coarse(feat_c0, feat_c1, mask_c0, mask_c1)

我们把刚刚1/8的特征图拿过来进行Transform。首先加上位置编码，位置编码我就不详说了，是Transform的基础内容了，用正余弦往里加就完事了。rearrange(x,'n c h w -> n (h w) c')会将原本的 h和 w 两个维度合并为一个维度 (h×w)，那么我们原来的feat_c0和feat_c1由(1,256,60,80)转为(1,4800,256)。mask是在训练过程有的东西，咱们不看，直接进入self.loftr_coarse()。

def forward(self, feat0, feat1, mask0=None, mask1=None):
    assert self.d_model == feat0.size(2), "the feature number of src and transformer must be equal"

    for layer, name in zip(self.layers, self.layer_names):
        if name == 'self':
            feat0 = layer(feat0, feat0, mask0, mask0)
            feat1 = layer(feat1, feat1, mask1, mask1)
        elif name == 'cross':
            feat0 = layer(feat0, feat1, mask0, mask1)
            feat1 = layer(feat1, feat0, mask1, mask0)
        else:
            raise KeyError

    return feat0, feat1

这里的self.layer_names值为['self', 'cross', 'self', 'cross', 'self', 'cross', 'self', 'cross']，这不就是我刚刚说的，重复做self->cross，这里重复了四次。self是自己跟自己做Transform，cross是两张图互相的Transform。我们进入layer看看这么个事。

def forward(self, x, source, x_mask=None, source_mask=None):
    bs = x.size(0)
    query, key, value = x, source, source

    # multi-head attention
    query = self.q_proj(query).view(bs, -1, self.nhead, self.dim)  # [N, L, (H, D)]
    key = self.k_proj(key).view(bs, -1, self.nhead, self.dim)  # [N, S, (H, D)]
    value = self.v_proj(value).view(bs, -1, self.nhead, self.dim)
    message = self.attention(query, key, value, q_mask=x_mask, kv_mask=source_mask)  # [N, L, (H, D)]
    message = self.merge(message.view(bs, -1, self.nhead * self.dim))  # [N, L, C]
    message = self.norm1(message)

    # feed-forward network
    message = self.mlp(torch.cat([x, message], dim=2))
    message = self.norm2(message)

    return x + message

在做self时，x和source是一样的。这里的q_proj、k_proj 和 v_proj是线性投影层，用于将输入映射到 query、key 和 value 的空间。

self.q_proj = nn.Linear(d_model, d_model, bias=False)
self.k_proj = nn.Linear(d_model, d_model, bias=False)
self.v_proj = nn.Linear(d_model, d_model, bias=False)

然后我们view一下，将原来256个dim分配到每个注意力头上。比如我们有8个注意力头，每个头分配256/8=32个dim，那么query、key 和 value的维度为(1,4800,8,32)。

是时候调用多头注意力模块attention，计算一下query、key 和 value之间的关系了，这里用的不是传统的注意力机制，而是线性注意力机制。传统的注意力机制通过Q和K 内积计算每个查询对键的相关性，并通过归一化（比如 softmax）得到权重，然后将权重应用于 V，生成输出。公式如下图。

而线性注意力机制，我们进去看看怎么个事。

def forward(self, queries, keys, values, q_mask=None, kv_mask=None):
    """ Multi-Head linear attention proposed in "Transformers are RNNs"
    Args:
        queries: [N, L, H, D]  n:样本数  l:序列长度  h:头数  d:维度
        keys: [N, S, H, D]  s:序列长度
        values: [N, S, H, D]
        q_mask: [N, L]
        kv_mask: [N, S]
    Returns:
        queried_values: (N, L, H, D)
    """
    Q = self.feature_map(queries)
    K = self.feature_map(keys)

    # set padded position to zero
    if q_mask is not None:
        Q = Q * q_mask[:, :, None, None]
    if kv_mask is not None:
        K = K * kv_mask[:, :, None, None]
        values = values * kv_mask[:, :, None, None]

    v_length = values.size(1)
    values = values / v_length  # prevent fp16 overflow
    # K(n, s, h, d)和values(n, s, h, v)按位加权合并 -> (n, h, d, v) 计算每个位置K和values的加权积，按头h和维度d结合，得到 KV
    KV = torch.einsum("nshd,nshv->nhdv", K, values)  # (S,D)' @ S,V
    # K沿序列长度s进行求和 -> (n, h, d) 然后计算Q和K的点积，得到一个加权值(n, l, h) -> 反映了 Q 和 K 之间的相似度
    Z = 1 / (torch.einsum("nlhd,nhd->nlh", Q, K.sum(dim=1)) + self.eps)
    # 根据Z对KV进行加权，并得到最终的查询结果
    queried_values = torch.einsum("nlhd,nhdv,nlh->nlhv", Q, KV, Z) * v_length

    return queried_values.contiguous()

主要是最后三行代码。

KV的计算：对于每个头 h，对键 K 和值 V 的每个位置 s 逐元素相乘（点积），然后沿序列长度 S 累加，得到形状为 [H,D,V] 的全局上下文矩阵。比如，K的维度[4800, 32]，D的维度[4800, 32]，K与D点积之后得到[32,32]，不过这里有8个头，所以最后得到的结果是[8,32,32]。

Z的计算：首先对键 K 在序列长度 S 上累加，得到形状为 [H,D] 的向量表示（每个头的全局表示）。然后，计算查询 Q 与键 K 的点积（沿维度 D），结果形状为 [L,H]。最后，取倒数并加上一个小值 ϵ 防止数值溢出。比如，K的维度[4800, 32]，在序列长度 S 上累加得到[1，32]，Q的维度[4800, 32]，Q 与 K 点积得到[4800，1]，不过这里有8个头，所以最后得到的结果是[4800,8]。

查询结果的计算：Q 与全局上下文 KV 按维度 D 相乘，结果形状为 [L,H,V]。使用归一化因子 Z 对结果加权，得到归一化后的查询值。比如，Q的维度[4800, 32]，KV的维度是[32,32]，Q和KV的点积为[4800,32]，再乘上权重Z得到[4800,32]，不过这里有8个头，所以最后得到的结果是[4800,8,32]。

根据我的了解，传统注意力机制的复杂度是 O(L^2)（因为要计算每个 Q 和 K 的点积）,而线性注意力机制的方法通过提前计算 KV，把复杂度降到了 O(L)。详细可以看这篇论文Transformers are RNNs: Fast Autoregressive Transformers with Linear Attention。

注意力机制给我的感觉就是两矩阵做内积，就可以算出这两矩阵的关系了，但是你要问我为什么做内积能得到它两的关系，我也说不上来（学艺不精，就来献丑）。我只能大致给个感觉，比如两向量如果垂直，那相乘就是0，表示这两向量没啥关系。如果这两向量的夹角非常小，那相乘就越大，表示这两向量脱不了干系。如果直接重合了（夹角为0），那咱俩简直就是一个东西啊。

最终我们完成了第二部分的任务，如下图。

3、粗粒度匹配

# 3. match coarse-level
self.coarse_matching(feat_c0, feat_c1, data, mask_c0=mask_c0, mask_c1=mask_c1)

我们进去看看怎么个事。

def forward(self, feat_c0, feat_c1, data, mask_c0=None, mask_c1=None):
    N, L, S, C = feat_c0.size(0), feat_c0.size(1), feat_c1.size(1), feat_c0.size(2)

    # normalize
    feat_c0, feat_c1 = map(lambda feat: feat / feat.shape[-1] ** .5,
                           [feat_c0, feat_c1])

    if self.match_type == 'dual_softmax':
        sim_matrix = torch.einsum("nlc,nsc->nls", feat_c0,  # 计算特征图1与特征图2上每个点的关系
                                  feat_c1) / self.temperature
        if mask_c0 is not None:
            sim_matrix.masked_fill_(
                ~(mask_c0[..., None] * mask_c1[:, None]).bool(),
                -INF)
        conf_matrix = F.softmax(sim_matrix, 1) * F.softmax(sim_matrix, 2)  # 转为概率

    elif self.match_type == 'sinkhorn':
        # sinkhorn, dustbin included
        sim_matrix = torch.einsum("nlc,nsc->nls", feat_c0, feat_c1)
        if mask_c0 is not None:
            sim_matrix[:, :L, :S].masked_fill_(
                ~(mask_c0[..., None] * mask_c1[:, None]).bool(),
                -INF)

        # build uniform prior & use sinkhorn
        log_assign_matrix = self.log_optimal_transport(
            sim_matrix, self.bin_score, self.skh_iters)
        assign_matrix = log_assign_matrix.exp()
        conf_matrix = assign_matrix[:, :-1, :-1]

        # filter prediction with dustbin score (only in evaluation mode)
        if not self.training and self.skh_prefilter:
            filter0 = (assign_matrix.max(dim=2)[1] == S)[:, :-1]  # [N, L]
            filter1 = (assign_matrix.max(dim=1)[1] == L)[:, :-1]  # [N, S]
            conf_matrix[filter0[..., None].repeat(1, 1, S)] = 0
            conf_matrix[filter1[:, None].repeat(1, L, 1)] = 0

        if self.config['sparse_spvs']:
            data.update({'conf_matrix_with_bin': assign_matrix.clone()})

    data.update({'conf_matrix': conf_matrix})

    # predict coarse matches from conf_matrix
    data.update(**self.get_coarse_match(conf_matrix, data))

sim_matrix就是特征图A上每个点与特征图B上每个点的乘积，所以得到[4800,4800]的矩阵，即特征图A与特征图B上每个点与每个点之间的关系。公式如下。

然后经过两个softmax，第一层 Softmax 是对行进行归一化，得到每个查询（Q）相对于所有键（K）的分布。第二层 Softmax 是对列进行归一化，得到每个键（K）相对于所有值（V）的分布。最后按元素相乘，是想得到一个同时考虑行和列信息的加权相似度矩阵conf_matrix，即软相互最近邻匹配的概率。公示如下。

得到了两个特征图之间的匹配概率，我们要开始粗粒度的挑选了。跳入到self.get_coarse_match()看看。

# 1. confidence thresholding
mask = conf_matrix > self.thr  # 大于0.2的才会被保存下来
mask = rearrange(mask, 'b (h0c w0c) (h1c w1c) -> b h0c w0c h1c w1c',
                 **axes_lengths)
if 'mask0' not in data:  # 对边界数据做个处理
    mask_border(mask, self.border_rm, False)
else:
    mask_border_with_padding(mask, self.border_rm, False,
                             data['mask0'], data['mask1'])
mask = rearrange(mask, 'b h0c w0c h1c w1c -> b (h0c w0c) (h1c w1c)',
                 **axes_lengths)

首先设置个门槛，匹配概率小于self.thr的塑料关系被踢掉。下面是对边界数据做个处理，不管。

# 2. mutual nearest  咱们两得都最最好才能被留下
mask = mask \
       * (conf_matrix == conf_matrix.max(dim=2, keepdim=True)[0]) \
       * (conf_matrix == conf_matrix.max(dim=1, keepdim=True)[0])

保留每一行的最大值，保留每一列的最大值，通过这两个条件结合，最终的mask只会保留那些同时是所在行和所在列的最大值的位置，即特征图AB看看你跟我最好的是不是我跟你最好的，只有咱们两得都最最好才能被留下。

# 3. find all valid coarse matches
# this only works when at most one `True` in each row
mask_v, all_j_ids = mask.max(dim=2)  # 找到相互匹配的位置
b_ids, i_ids = torch.where(mask_v)  # B图j的位置与A图i的位置匹配
j_ids = all_j_ids[b_ids, i_ids]  
mconf = conf_matrix[b_ids, i_ids, j_ids]  # 它们匹配的概率值

寻找剩下有效的的粗匹配，找到特征图A与特征图B匹配的索引位置。

最终我们完成了第三部分的任务，如下图。

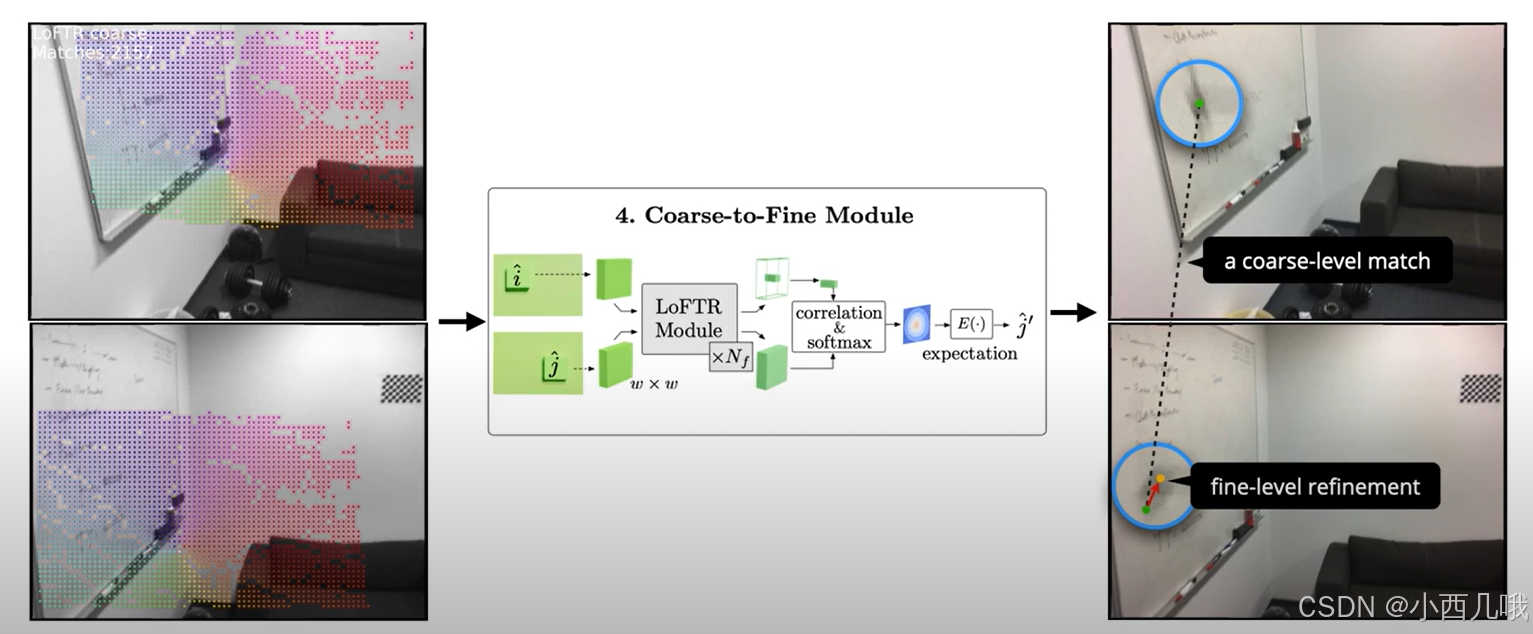
4、细粒度匹配

# 4. fine-level refinement
feat_f0_unfold, feat_f1_unfold = self.fine_preprocess(feat_f0, feat_f1, feat_c0, feat_c1, data)
if feat_f0_unfold.size(0) != 0:  # at least one coarse level predicted
    feat_f0_unfold, feat_f1_unfold = self.loftr_fine(feat_f0_unfold, feat_f1_unfold)

首先对特征图进行一个预处理操作，self.fine_preprocess()传入的是一开始backbone提取的1/2的特征图和，跳进去看看怎么个事。

def forward(self, feat_f0, feat_f1, feat_c0, feat_c1, data):
    W = self.W
    stride = data['hw0_f'][0] // data['hw0_c'][0]

    data.update({'W': W})
    if data['b_ids'].shape[0] == 0:
        feat0 = torch.empty(0, self.W ** 2, self.d_model_f, device=feat_f0.device)
        feat1 = torch.empty(0, self.W ** 2, self.d_model_f, device=feat_f0.device)
        return feat0, feat1

    # 1. unfold(crop) all local windows
    feat_f0_unfold = F.unfold(feat_f0, kernel_size=(W, W), stride=stride, padding=W // 2)  # 3200 = 5*5*128
    feat_f0_unfold = rearrange(feat_f0_unfold, 'n (c ww) l -> n l ww c', ww=W ** 2)
    feat_f1_unfold = F.unfold(feat_f1, kernel_size=(W, W), stride=stride, padding=W // 2)
    feat_f1_unfold = rearrange(feat_f1_unfold, 'n (c ww) l -> n l ww c', ww=W ** 2)

    # 2. select only the predicted matches
    feat_f0_unfold = feat_f0_unfold[data['b_ids'], data['i_ids']]  # [n, ww, cf]
    feat_f1_unfold = feat_f1_unfold[data['b_ids'], data['j_ids']]

    # option: use coarse-level loftr feature as context: concat and linear
    if self.cat_c_feat:
        feat_c_win = self.down_proj(torch.cat([feat_c0[data['b_ids'], data['i_ids']],
                                               feat_c1[data['b_ids'], data['j_ids']]], 0))  # [2n, c]
        feat_cf_win = self.merge_feat(torch.cat([
            torch.cat([feat_f0_unfold, feat_f1_unfold], 0),  # [2n, ww, cf]
            repeat(feat_c_win, 'n c -> n ww c', ww=W ** 2),  # [2n, ww, cf]
        ], -1))
        feat_f0_unfold, feat_f1_unfold = torch.chunk(feat_cf_win, 2, dim=0)

    return feat_f0_unfold, feat_f1_unfold

F.unfold()就是我开头说的对1/2的特征图做区域匹配，而不是点匹配。比如我们输入的feat_f0维度是(1,128,240,320)，经过F.unfold()，假设kernel_size=(5, 5)，stride=4，padding=2，那么输出feat_f0_unfold维度是(1,3200,4800)。这个3200不重要，反正后面还要进行rearrange给它展回去，展成(4800,25,128)。这边就直观多了5×5×128=3200，4800跟卷积那个计算是一样的，这个很基础应该不用我多说了吧。

F.unfold()有点像卷积，但又不是卷积，毕竟形式上感觉是一样的，都有kernel_size、stride和padding这些东西。不过F.unfold()是不做计算的，只负责提取滑动窗口的内容然后展开，而卷积会对每个窗口内的值和卷积核进行点积计算，输出新的值。为了帮助大家理解，我画了一张图如下。

处理完1/2的特征图后，巧了，我也有4800条数据你也有4800条数据，我们可以做个匹配啦。之前粗粒度最后得到了匹配的特征图A的索引位置i与特征图B的索引位置j，所以将有效的索引传入，最终得到有效匹配区域feat_f0_unfold和feat_f1_unfold。

最后对feat_f0_unfold和feat_f1_unfold做注意力机制，self.loftr_fine(feat_f0_unfold, feat_f1_unfold)，和之前的一样的我就不多说了。

最终我们完成了第四部分的任务，如下图。

5、通过期望计算得到最终输出

终于到第五步了，写累死我了k。

def forward(self, feat_f0, feat_f1, data):
    M, WW, C = feat_f0.shape
    W = int(math.sqrt(WW))
    scale = data['hw0_i'][0] / data['hw0_f'][0]
    self.M, self.W, self.WW, self.C, self.scale = M, W, WW, C, scale

    # corner case: if no coarse matches found
    if M == 0:
        assert self.training == False, "M is always >0, when training, see coarse_matching.py"
        # logger.warning('No matches found in coarse-level.')
        data.update({
            'expec_f': torch.empty(0, 3, device=feat_f0.device),
            'mkpts0_f': data['mkpts0_c'],
            'mkpts1_f': data['mkpts1_c'],
        })
        return

    feat_f0_picked = feat_f0[:, WW // 2, :]
    sim_matrix = torch.einsum('mc,mrc->mr', feat_f0_picked, feat_f1)
    softmax_temp = 1. / C ** .5
    heatmap = torch.softmax(softmax_temp * sim_matrix, dim=1).view(-1, W, W)

    # compute coordinates from heatmap
    coords_normalized = dsnt.spatial_expectation2d(heatmap[None], True)[0]  # [M, 2]
    grid_normalized = create_meshgrid(W, W, True, heatmap.device).reshape(1, -1, 2)  # [1, WW, 2]

    # compute std over <x, y>
    var = torch.sum(grid_normalized ** 2 * heatmap.view(-1, WW, 1), dim=1) - coords_normalized ** 2  # [M, 2]
    std = torch.sum(torch.sqrt(torch.clamp(var, min=1e-10)), -1)  # [M]  clamp needed for numerical stability

    # for fine-level supervision
    data.update({'expec_f': torch.cat([coords_normalized, std.unsqueeze(1)], -1)})

    # compute absolute kpt coords
    self.get_fine_match(coords_normalized, data)

就像我开头说的那样，匹配上了区域，但具体是区域的哪个点呢？我们再细化一下。

首先找到区域的中心点feat_f0_picked，然后我们计算中心点与区域其它点的一个关系。关系怎么算来着，就是矩阵内积，算出sim_matrix。比如feat_f0_picked的维度是(100,128)，feat_f1的维度是(100,25,128)，其中100是匹配上的区域，25是5×5的区域，128是dim，做完内积得到sim_matrix(100,25)。给它softmax一下，计算它的概率heatmap(100,5,5)。得到了这个区域的热力图，我怎么知道具体往哪偏呢？计算它的期望，得到它的实际位置coords_normalized(100,2)，2就是它xy的实际坐标了。后面就是将coords_normalized还原到原始的位置当中，根据特征图大小的一个比例还原回去。

最终我们完成了第五部分的任务，如下图。