Lane Detection车道线检测模型（附源码+论文）

Lane Detection车道线检测模型

代码链接：Lane_Detection-study（关键部分注释详细）

论文链接：Ultra Fast Structure-aware Deep Lane Detection

官方链接：Lane-Detection

数据集	链接
CULane	GoogleDrive/BaiduDrive(code:w9tw)
Tusimple	GoogleDrive/BaiduDrive(code:bghd)

看看效果

总体流程

这个模型的话，网络方面特别简单，毕竟论文题目有个Fast，那网络肯定得简单，越简单越快嘛。不过数据处理那块有点复杂，然后再自定义点适合这个任务的损失函数。我们先简单过一遍流程，然后在代码里详细说。

还是老规矩，先输入一个图像然后放到backbone里提取特征（现在模型基本都是这个起步，雷打不动），这里又是我们的老朋友ResNet。接两条支路，上面的是辅助分割，下面的是分类。有没有觉得很奇怪，车道检测怎么都感觉应该用回归做，直接预测车道的位置坐标，但是作者用的是分类而且给出了解释。

上图可以看出，回归的准确率七十左右，而分类的准确率有九十几，这差距有点大的。你要问为什么，实验得真理。

上面那条支路我为什么说辅助分割而不是分割呢？还是那个词Fast！这个分割任务只在训练阶段做，而测试阶段会被移除。辅助分割在训练阶段给分类提供了更多监督信息，让模型更精确地识别车道线。训练结束，分类器已经是个训练有素的牛马了，因此在测试阶段可以一脚给辅助分割蹬掉（教会徒弟，饿死师傅），少了师傅这个慢工出细活的拖油瓶，推理过程直接提速。

论文题目中的Fast不仅展现在网络上，对数据的处理上也有点手段的。我们先来看看标签图是怎么个事。

上图就是原图和它的标签图。标签图看上去一片漆黑，我当时打开标签图文件夹的时候，里面所有的图片都是黑的，一脸懵逼，我以为下载出错了呢。里面还是有值的，只是看不见，到时候会读取它，一会代码里详说。

这个乌黑的图片里是有车道的标识的，视情况而定有几条，最多是4条车道线。我们先要对这个车道线做个预处理。

从上图可以看见哈，作者对车道线做了一个增强，将车道线扩展到了图片的边界处，而不是局限于中间那部分。

上面说的，检测车道用的是分类的方法，那对每个像素点问它：“你是车道线不？概率多大啊？”，这计算量，不言而喻了。作者灵机一动，这车道线的位置其实还蛮固定的（因为摄像头的位置是固定的），有些地方明显就不可能有车道线，我给它整个先验信息吧。

预测一条线，太费事了，给改为预测18个点。这18个点的纵坐标吧，不是很固定，要视情况而定，比如一个拐弯就飘没了。但是它的横坐标，基本不会变化，所以我们先给它定死18个横坐标。好，横坐标确定了我们再来分析它的纵坐标。这18个点吧，它也不是定死的一个像素点位置，那个像素点的一定范围内其实都是车道线。所以我们放宽松，将当前的宽给划分为200个格子。这时候问题就从判断每个像素点是不是车道线，转变为这18行里的200个格子是车道线的概率。（这里的18、200不是固定的，你可以自己调整）

代码

数据处理

先进入dataset.py的LaneClsDataset中。

def __getitem__(self, index):
    l = self.list[index]  # 数据路径和标签路径
    l_info = l.split()
    img_name, label_name = l_info[0], l_info[1]
    if img_name[0] == '/':
        img_name = img_name[1:]
        label_name = label_name[1:]

    label_path = os.path.join(self.path, label_name)
    label = loader_func(label_path)

    img_path = os.path.join(self.path, img_name)
    img = loader_func(img_path)

    if self.simu_transform is not None:
        img, label = self.simu_transform(img, label)  # 数据增强
    lane_pts = self._get_index(label)
    # get the coordinates of lanes at row anchors

    w, h = img.size
    cls_label = self._grid_pts(lane_pts, self.griding_num, w)  # 相当于将lane_pts映射到griding_num个格子里
    # make the coordinates to classification label
    if self.use_aux:
        assert self.segment_transform is not None
        seg_label = self.segment_transform(label)

    if self.img_transform is not None:
        img = self.img_transform(img)

    if self.use_aux:
        return img, cls_label, seg_label
    if self.load_name:
        return img, cls_label, img_name
    return img, cls_labelme
        return img, cls_label

前面没什么好说的，就是读取路径，然后做一个简单是数据增强，比如旋转、垂直或水平移动什么的。主要是self._get_index(label)和self._grid_pts(lane_pts, self.griding_num, w)， 我们来看看怎么个事。

_get_index

我们先来看一下self._get_index(label)干了啥。

def _get_index(self, label):
    w, h = label.size

    if h != 288:  # 因为后续会给数据resize为288 先验值是按288做的
        scale_f = lambda x: int((x * 1.0 / 288) * h)
        sample_tmp = list(map(scale_f, self.row_anchor))  # 相当于一个先验值 18个车道点

    all_idx = np.zeros((self.num_lanes, len(sample_tmp), 2))  # (4, 18, 2) 4条车道线 18个车道点 2个行列位置 列为-1表示不存在
    for i, r in enumerate(sample_tmp):  # 遍历每个点 18
        label_r = np.asarray(label)[int(round(r))]  # 读取标签在这一行的所有信息
        for lane_idx in range(1, self.num_lanes + 1):  # 遍历每条车道线 4
            pos = np.where(label_r == lane_idx)[0]
            if len(pos) == 0:
                all_idx[lane_idx - 1, i, 0] = r  # 第几行
                all_idx[lane_idx - 1, i, 1] = -1  # -1为没有信息
                continue
            pos = np.mean(pos)  # 车道线是有宽度的 所以取个平均
            all_idx[lane_idx - 1, i, 0] = r  # 第几行
            all_idx[lane_idx - 1, i, 1] = pos  # 当前车道线列位置

    # data augmentation: extend the lane to the boundary of image

    all_idx_cp = all_idx.copy()
    for i in range(self.num_lanes):
        if np.all(all_idx_cp[i, :, 1] == -1):  # 判断车道存不存在
            continue
        # if there is no lane
        # 对4条车道进行一个延伸，如果不存在这条车道就不
        valid = all_idx_cp[i, :, 1] != -1  # 第i个车道线的18个车道点是否存在
        # get all valid lane points' index
        valid_idx = all_idx_cp[i, valid, :]  # 存在的点坐标
        # get all valid lane points
        if valid_idx[-1, 0] == all_idx_cp[0, -1, 0]:
            # 如果最后一个有效车道点的y坐标已经是所有行的最后一个y坐标
            # 这意味着这条线已经达到了图像的底部边界
            # 所以我们跳过
            continue
        if len(valid_idx) < 6:
            continue
        # 如果车道太短，无法延伸

        valid_idx_half = valid_idx[len(valid_idx) // 2:, :]  # 取后半段的车道点
        p = np.polyfit(valid_idx_half[:, 0], valid_idx_half[:, 1], deg=1)  # 线性拟合 延长这条线到边界
        start_line = valid_idx_half[-1, 0]  # 取后半段车道点中最后一个点的 x 坐标作为起点，用于后续查找和拟合
        pos = find_start_pos(all_idx_cp[i, :, 0], start_line) + 1  # 找到 start_line 的索引位置

        fitted = np.polyval(p, all_idx_cp[i, pos:, 0])  # 得到拟合值
        fitted = np.array([-1 if y < 0 or y > w - 1 else y for y in fitted])  # 判断拟合值能否放进图中 -1表示无效

        assert np.all(all_idx_cp[i, pos:, 1] == -1)
        all_idx_cp[i, pos:, 1] = fitted  # 放进下一个位置
    if -1 in all_idx[:, :, 0]:
        pdb.set_trace()
    return all_idx_cp

因为后面会将原图给Resize成288×800，所以标签也是按这个格式做的。self.row_anchor就是一个定死的先验值，在constant.py里，如果用的是culane的数据集那就是18个点的横坐标。为了方便理解，我后面都假设车道线的行坐标有18条。

tusimple_row_anchor = [ 64,  68,  72,  76,  80,  84,  88,  92,  96, 100, 104, 108, 112,
            116, 120, 124, 128, 132, 136, 140, 144, 148, 152, 156, 160, 164,
            168, 172, 176, 180, 184, 188, 192, 196, 200, 204, 208, 212, 216,
            220, 224, 228, 232, 236, 240, 244, 248, 252, 256, 260, 264, 268,
            272, 276, 280, 284]
culane_row_anchor = [121, 131, 141, 150, 160, 170, 180, 189, 199, 209, 219, 228, 238, 248, 258, 267, 277, 287]

比如你原图高度是590，会将这先验值映射到到0-590里（因为原先的先验值是按0-288定的），得到实际的位置sample_tmp。

然后我们遍历标签图里的这18行，标签图里最多会有5种值（0-无车道，1-第一条车道，2-第二条车道，3-第三条车道，4-第四条车道）。寻找这18行里有没有车道线，如果没有的话赋值-1，如果有的话记录它的列坐标。因为车道是有一定宽度的，所以会取平均值作为列坐标。最终得到all_idx，维度为(4, 18, 2)，分别表示4条车道线，18个车道点，2个行列位置。

比如下图就表示图中第一条车道的信息。第一列表示18个车道点的行坐标，第二列表示纵坐标，-1表示这一行没找到车道线。

然后我们根据all_idx对车道线进行延伸，延伸至图边界。当然要做一些判断，比如有没有这条车道，或者这车道点少于6个也太短了不延伸。如果最后一个有效车道点的y坐标已经是所有行的最后一个y坐标，这意味着这条线已经达到了图像的底部边界，直接跳过。

对于剩下需要做延伸的车道，我们对车道点进行线性拟合（因为有些车道是弯的，不能直接画过去），拟合后得到的值再判断一下能不能放到图中，如果不合规就扔掉（赋值-1）。

最终得到all_idx_cp，包含了延伸后的车道点信息，维度为(4,18,2)。

_grid_pts

我们再来看一下self._grid_pts(lane_pts, self.griding_num, w)干了啥。

def _grid_pts(self, pts, num_cols, w):
    # pts : numlane,n,2
    num_lane, n, n2 = pts.shape
    col_sample = np.linspace(0, w - 1, num_cols)  # 将宽分为num_cols个格子

    assert n2 == 2
    to_pts = np.zeros((n, num_lane))
    for i in range(num_lane):  # 遍历每个车道线
        pti = pts[i, :, 1]
        to_pts[:, i] = np.asarray(
            [int(pt // (col_sample[1] - col_sample[0])) if pt != -1 else num_cols for pt in pti])
    return to_pts.astype(int)

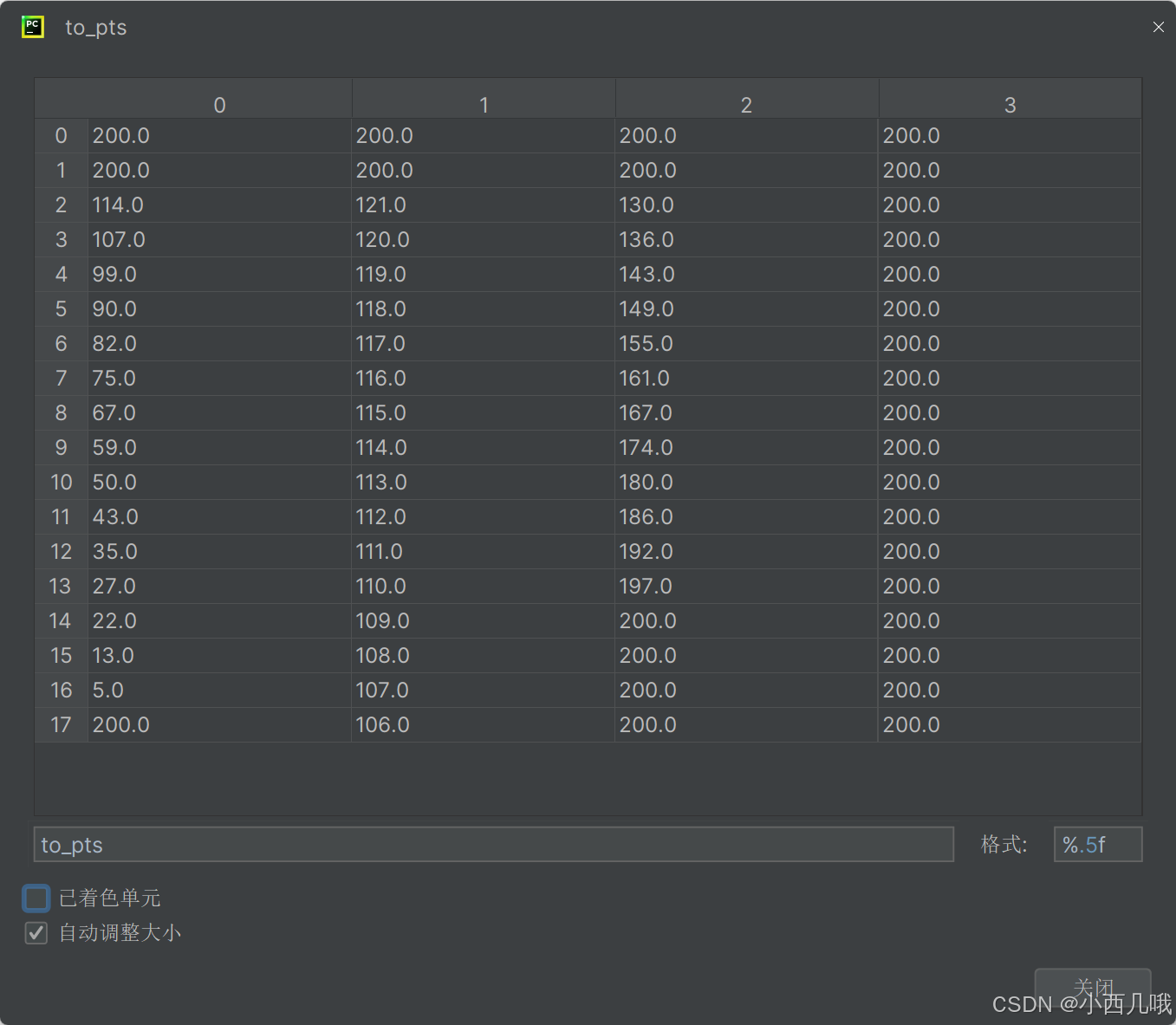
先获得图片的宽，然后给分割成200块。接着遍历每条车道线，判断一下它属于哪个格子。这里一共有201个值（0-200），200表示这行没有车道，其余值表示这行的车道点在哪个格子，如下图所示。最终得到to_pts，维度为（18,4）。

model

我们再看看看网络部分怎么搞的，在model.py的parsingNet的forward。

def forward(self, x):  # (B, 3, 288, 800)
    # n c h w - > n 2048 sh sw
    # -> n 2048
    x2, x3, fea = self.model(x)  # x2(B, 128, 36, 100) x3(B, 256, 18, 50) fea(B, 512, 9, 25)  # backbone提取特征
    if self.use_aux:  # 这里做的是辅助分割
        x2 = self.aux_header2(x2)  # (B, 128, 36, 100)
        x3 = self.aux_header3(x3)  # (B, 128, 18, 50)
        x3 = torch.nn.functional.interpolate(x3, scale_factor=2, mode='bilinear')  # (B, 128, 36, 100)
        x4 = self.aux_header4(fea)  # (B, 128, 9, 25)
        x4 = torch.nn.functional.interpolate(x4, scale_factor=4, mode='bilinear')  # (B, 128, 36, 100)
        aux_seg = torch.cat([x2, x3, x4], dim=1)  # (B, 384, 9, 25)
        aux_seg = self.aux_combine(aux_seg)  # (B, 5, 36, 100)
    else:
        aux_seg = None

    fea = self.pool(fea).view(-1, 1800)  # (B, 8, 9, 25) -> (B, 1800)

    group_cls = self.cls(fea).view(-1, *self.cls_dim)  # (B, 201, 18, 4) 201个分类 18个车道点 4个车道线

    if self.use_aux:
        return group_cls, aux_seg

    return group_cls

第一块self.model(x)不用说了吧，就是backbone提取的三层特征图。

在辅助分割里，self.aux_header都是基本的卷积（conv->bn->relu)，做好几个卷积然后上采样一下再做好几个卷积，最后给拼接在一起做几个卷积得到最后的aux_seg。

分类就更简单了，self.pool就是个基本的conv，self.cls就是两个全连接层（Linear->relu->Linear）。最后全连接层输出14472个值，在view为(B,201,18,4)，分别表示201个分类，18个车道点和 4条车道线。

loss

最后就是我们的损失函数了，进入loss.py看看。

SoftmaxFocalLoss

def forward(self, logits, labels):
    scores = F.softmax(logits, dim=1)
    factor = torch.pow(1. - scores, self.gamma)  # 权重 样本预测误差越小权重越小 误差越大权重越大
    log_score = F.log_softmax(logits, dim=1)  # 交叉熵
    log_score = factor * log_score
    loss = self.nll(log_score, labels)
    return loss

这个就是分类损失，稍微做了一点改进。我们看到这里计算了一个factor，这有什么影响呢。比如你预测这个车道点有0.95的可能是的，这块训练的非常不错，不需要重点关注了，给你一个小点的权重吧，((1-0.95)×2)^2=0.01。预测的另一个车道点有0.65的可能是，这个就有点没把握了啊，你这块训练的不行啊，得多关注关注啊，也给你一个大点的权重吧，((1-0.65)×2)^2=0.49。这样模型会更多关注训练不好的地方，其实就是焦点损失（Focal Loss） 的思想

ParsingRelationLoss

def forward(self, logits):
    n, c, h, w = logits.shape  # (B, 201, 18, 4)
    loss_all = []
    for i in range(0, h - 1):
        loss_all.append(logits[:, :, i, :] - logits[:, :, i + 1, :])  # 两个相邻的车道点概率接近
    # loss0 : n,c,w
    loss = torch.cat(loss_all)
    return torch.nn.functional.smooth_l1_loss(loss, torch.zeros_like(loss))

由于车道是连续的，即相邻行的车道点应该彼此接近。因此，通过约束分类向量在邻行上的分布来实现连续性，公式如下。

ParsingRelationDis

def forward(self, x):
    n, dim, num_rows, num_cols = x.shape  # (B, 201, 18, 4) 200个位置的概率+最后一个判断有没有车道线
    x = torch.nn.functional.softmax(x[:, :dim - 1, :, :], dim=1)  # (B, 200, 18, 4)  最后一个去掉了
    embedding = torch.Tensor(np.arange(dim - 1)).float().to(x.device).view(1, -1, 1, 1)
    pos = torch.sum(x * embedding, dim=1)  # 求期望(直接取最大值没办法反向传播)

    diff_list1 = []
    for i in range(0, num_rows // 2):
        diff_list1.append(pos[:, i, :] - pos[:, i + 1, :])  # 两个相邻的车道点位置接近

    loss = 0
    for i in range(len(diff_list1) - 1):
        loss += self.l1(diff_list1[i], diff_list1[i + 1])
    loss /= len(diff_list1) - 1
    return loss

车道线通常是直线，或在曲线部分也会由于透视效应表现为直线，因此可以使用二阶差分方程来约束车道线的形状。直线车道线的二阶差分结果为零。车道线位置的计算是找到这行里分类预测的最大值。公式如下。

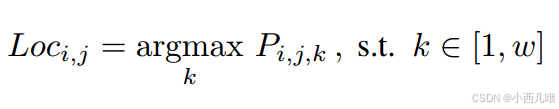
但是有个问题，就是argmax函数是不可微的，没法反向传播。所以作者用预测的期望作为位置的近似值。公示如下。

diff_list1存储的是相邻车道点之间的位置差异。得到了相邻位置差异就可以计算它们的二阶差分了。self.l1(diff_list1[i], diff_list1[i + 1]) 计算相邻两个差异之间的 L1 损失。这里计算的是 二阶差分，即通过计算相邻车道点之间的差异，再对这些差异的差异进行惩罚，迫使车道线更加平滑。公式如下。

通过约束相邻车道点的位置接近，促进车道线的平滑性，进而引导模型预测连续、平滑的车道线。

demo

最后在demo里配置自己的.pth文件和测试数据就行。

if cfg.dataset == 'CULane':
    # splits = ['test0_normal.txt', 'test1_crowd.txt', 'test2_hlight.txt', 'test3_shadow.txt', 'test4_noline.txt', 'test5_arrow.txt', 'test6_curve.txt', 'test7_cross.txt', 'test8_night.txt']
    splits = ['mytest.txt']
    datasets = [LaneTestDataset(cfg.data_root, os.path.join(cfg.data_root, 'list/test_split/' + split),
                                img_transform=img_transforms) for split in splits]
    img_w, img_h = 1640, 590
    row_anchor = culane_row_anchor

例如我就是用的CULane，然后将splits改为我自己的mytest.txt。给你们看一下我的mytest.txt。

我自己的mytest.txt和代码里注释的都在CULane\list\test_split路径下，大家可以自己改。

=======================================================================================================

最近买了个新玩具Jetson Nano，就是一个开发板，可以部署人工智能的模型的。开发板是基于ubuntu的，我正好也想玩玩linux系统，因为好多模型都是基于linux不支持windows。开发板前天刚到手，这两天算是给我逼疯了，疯狂踩坑，安装系统，部署docker简直各种bug。如果是我哪里的配置出错了我都认，最顶不住的就是我找了半天的问题最后发现是版本不对，两眼一黑…

万事开头难吧，慢慢度过这个困难期