Geometric camera calibration
相机模型
本节描述常见的相机模型。主要关注中心相机,也就是具有单一有效视点的相机。单视点意味着到达图像的所有光线都穿过空间中的单个点,即焦点。
透视相机
针孔相机模型是最常见的相机模型,对于大多数服从透视模型的传统相机来说,这是一个相当合理的近似模型。通常,这些相机具有小于60°的小视场。本质上,针孔相机模型只是一个透视投影,然后是图像平面中的仿射变换。

相机坐标系(3D)到像平面坐标系(2D)的齐次变换可用3x4投影矩阵表示
Z
c
(
x
y
1
)
=
[
f
0
0
0
0
f
0
0
0
0
1
0
]
(
X
c
Y
c
Z
c
1
)
Z_c\begin{pmatrix} x\\ y\\ 1 \end{pmatrix} = \begin{bmatrix} f& 0& 0 & 0\\ 0& f& 0 & 0\\ 0& 0& 1 & 0 \end{bmatrix}\begin{pmatrix} X_c\\ Y_c\\ Z_c \\ 1 \end{pmatrix}
Zc⎝⎛xy1⎠⎞=⎣⎡f000f0001000⎦⎤⎝⎜⎜⎛XcYcZc1⎠⎟⎟⎞
像平面坐标系到像素坐标系变换:
(
u
v
)
=
[
m
u
−
m
u
cot
α
0
m
v
sin
α
]
(
x
y
)
+
(
u
0
v
0
)
\begin{pmatrix} u\\ v \end{pmatrix} = \begin{bmatrix} m_u& -m_u\cot \alpha\\ 0& \frac{m_v}{\sin \alpha} \end{bmatrix}\begin{pmatrix} x\\ y \end{pmatrix}+\begin{pmatrix} u_0\\ v_0 \end{pmatrix}
(uv)=[mu0−mucotαsinαmv](xy)+(u0v0)
α \alpha α是轴u和v的夹角,传统相机一般是90°。 m u m_u mu和 m v m_v mv是轴u和v方向上每单位距离内的像素数量。
联立起来,得到世界坐标系到像素坐标系的变换公式:

m
u
f
m_u f
muf是一起变化的,优化时直接合在一起。
s
=
−
cot
α
s=-\cot \alpha
s=−cotα;
γ
=
m
v
m
u
sin
α
\gamma=\frac{m_v}{m_u\sin \alpha}
γ=musinαmv。简化为:
1
Z
c
(
u
v
1
)
=
[
f
s
f
u
0
0
γ
f
v
0
0
0
1
]
[
R
t
]
(
X
c
Y
c
Z
c
)
\frac{1}{Z_c}\begin{pmatrix} u\\ v \\ 1 \end{pmatrix} =\begin{bmatrix} f& sf& u_0\\ 0& \gamma f& v_0\\ 0& 0& 1 \end{bmatrix} [\mathbf{R} \quad \mathbf{t}] \begin{pmatrix} X_c\\ Y_c\\ Z_c \end{pmatrix}
Zc1⎝⎛uv1⎠⎞=⎣⎡f00sfγf0u0v01⎦⎤[Rt]⎝⎛XcYcZc⎠⎞
由于一般
α
\alpha
α是90°,当轴u和v上的像素数相同时,s=0,
γ
=
1
\gamma=1
γ=1。不相同时保留
γ
\gamma
γ,进行优化。
简化写为内参和外参矩阵形式:
λ
(
u
v
1
)
=
K
[
R
t
]
(
X
c
Y
c
Z
c
)
\lambda \begin{pmatrix} u\\ v \\ 1 \end{pmatrix} = \mathbf{K} [\mathbf{R} \quad \mathbf{t}] \begin{pmatrix} X_c\\ Y_c\\ Z_c \end{pmatrix}
λ⎝⎛uv1⎠⎞=K[Rt]⎝⎛XcYcZc⎠⎞
其中3x4矩阵称为相机投影矩阵
P
=
K
[
R
t
]
\mathbf{P}=\mathbf{K} [\mathbf{R} \quad \mathbf{t}]
P=K[Rt]
正交相机??
透镜畸变
最重要的几何失真类型是径向失真,它导致给定图像点从其理想位置向内或向外位移。透镜元件的偏心导致附加的失真,该失真也具有切向分量。
透镜畸变的常用模型考虑了径向和偏心畸变。

这个模型在实际中无法使用,因此需要做调整。在文献1中,对畸变模型做了相应的调整: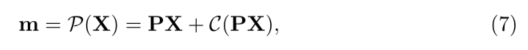
可以理解为理想投影+畸变影响,得到检测的像素坐标。它用了
κ
1
,
κ
2
,
ρ
1
,
ρ
2
\kappa_1, \kappa_2, \rho_1, \rho_2
κ1,κ2,ρ1,ρ2四个畸变参数。畸变中心假设与主点相同。
全向相机
针孔模型不适用于超过180°视场的全向相机的原因:入射光线与光轴接近90°时,透视投影将光线无限远地映射到图像中,并且不可能用上述失真模型去除这种奇异性。
折反射相机
在折反射全向相机中,通过在相机镜头前放置一面镜子来获得宽视场。在中心反折射照相机中,反射镜的形状和配置使得整个反折射系统具有单一有效视点。已经表明,产生单一视点的镜面是旋转曲面,其二维轮廓是圆锥截面。在真实的中心折反射相机中使用的实际有用的镜面是平面的、双曲线的、椭圆的和抛物线的。然而,平面镜不会改变摄像机的视场。

图2,中心折反射相机,分别具有双曲、椭圆和抛物面镜。Z轴是相机的光轴,也是镜面的旋转轴。场景点P成像在p点。在任何情况下,反折射系统的视点都是由焦距F表示的反射镜的焦点。在双曲和椭圆镜的情况下,透视相机的有效针孔必须放置在另一个焦点上,这里用
F
′
F^{'}
F′表示。
图2是折反射相机的几种配置。为了满足单视点约束,抛物面镜与正交摄像机相结合(图2-3),而其他的镜子与透视照相机结合在一起(图2-1,2-2)。
单视点反折射成像得到了很好的研究[9,10],并且已经表明,包括图2所示情况在内的中心反折射投影相当于通过单位球面的两步映射[10,11]。模型是一个组合函数:

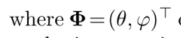 是入射光线的方向。这个过程是首先投影到单位球上,然后再投影到像平面上。图3显示了模型的原理。O是相机的有效视点。
l
l
l是内参数。
是入射光线的方向。这个过程是首先投影到单位球上,然后再投影到像平面上。图3显示了模型的原理。O是相机的有效视点。
l
l
l是内参数。

F
\mathcal{F}
F的形式为:
x
=
F
=
r
(
θ
)
(
cos
φ
sin
φ
)
\mathbf{x}=\mathcal{F}=r(\theta)\begin{pmatrix} \cos \varphi \\ \sin \varphi \end{pmatrix}
x=F=r(θ)(cosφsinφ)理解为投影点到光心的距离,在x、y轴上的分量。
r
r
r由
l
l
l决定,即
r
=
(
l
+
1
)
sin
θ
l
+
cos
θ
r=\frac{(l+1)\sin\theta}{l+\cos\theta}
r=l+cosθ(l+1)sinθ。这里还有一个隐含的相似三角形。
在具有双曲或椭圆反射镜的中心反折射系统中,相机轴不必与反射镜对称轴对齐。相机和镜子的轴通常接近共线, H \mathcal{H} H近似为放射变换,也就是 ( u v 1 ) ≅ K ( x 1 ) \begin{pmatrix}u\\v\\1\end{pmatrix}\cong\mathbf{K}\begin{pmatrix}\mathbf{x}\\1\end{pmatrix} ⎝⎛uv1⎠⎞≅K(x1)。 K \mathbf{K} K是透视相机的内参矩阵。
鱼眼透镜
由于不可能通过透视投影将半球形视场投影到有限的像平面上,鱼眼透镜被设计成服从一些其他的投影模型。
透视投影的表达式
r
=
tan
θ
r=\tan \theta
r=tanθ。r是像点到主点的距离,这里假设焦距
f
=
1
f=1
f=1。鱼眼镜通常设计为服从下面中的一个:

第三个是常用的模型。
虽然中心反折射相机和鱼眼相机有不同的物理结构,但从数学建模的角度来看,它们没有太大的不同。对径向对称中心摄像机建模的问题实质上被简化为对径向投影函数建模
中心相机的通用模型
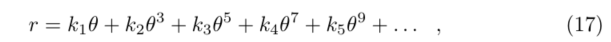
公式10和公式13、14、15、16的一个泰勒展开式,偶次项怎么没了?9次幂能够提供足够的自由度,近似不同的投影曲线。因此,通用模型的径向投影函数r具有5个参数。
然而,真实的透镜可能偏离精确的径向对称,因此,上面的径向对称模型在[2]中补充了一个不对称部分。用下式代替公式10,

这里径向和切向失真项都包含七个参数。
公式19中的不对称部分模拟了光学系统中的缺陷。然而,这里的目的不是对光学失真进行严格的建模,而是提供一个灵活的数学失真模型,该模型恰好与观察结果相一致。这种方法通常是实用的,因为光学系统中可能有几个可能的缺陷源,并且很难对所有这些缺陷进行详细建模。
有时,为了避免过度装配,省略不对称部分可能是有用的。
畸变模型
透视相机

鱼眼镜

非中心相机
大多数真相机严格来说是非中心的。例如,在图2中抛物面镜的情况下,很难精确地对准镜轴和照相机的轴。同样,在双曲和椭圆配置中,透视相机的光学中心在反射镜焦点中的精确定位实际上是不可行的。此外,如果镜子的形状不是圆锥曲线,或者真实的相机不是真正的正射或透视的,则配置是非中心的。然而,在实践中,与观察区域相比,摄像机通常小得可以忽略不计,因此它实际上是点状的。因此,中央摄像机模型被广泛使用,并且在大多数情况下都是站得住脚的,所以在本文中,我们也集中讨论中央摄像机。
尽管如此,仍有一些作品放松了单视点约束,使用了非中心相机模型。例如,在[18]和[19]中讨论了完全通用的摄像机校准方法,其中使用了非参数摄像机模型。在这个模型中,相机的每个像素与3D中的一条光线相关联,并且校准的任务是确定这些光线在某个局部坐标系中的坐标。此外,已经开展了为符合预定要求的非中心反折射系统设计镜子的工作[20]。
最后,作为中心相机的推广,我们想提到轴相机,其中所有的投影光线都穿过空间中的一条线[19]。例如,由一面镜子和一个中心照相机组成的反折射照相机,如果镜子是任何旋转表面,并且照相机中心位于镜子旋转轴线上,则是轴向照相机。中心摄像机是轴向摄像机的特例。等角[21,22]和等面[23]反折射相机是另一类轴向相机。在等面积相机中,投影是面积保持的,而等角镜被设计成从图像的对称中心测量的径向距离与入射光线和光轴之间的角度成线性比例。
标定方法
合适的校准算法的选择取决于摄像机模型,下面我们描述校准透视和全向中央摄像机的方法。尽管校准程序的细节可能因相机而异,但该程序的最后一步通常是通过非线性优化来细化相机参数,而不需考虑相机模型。在最小化中通常使用的成本函数是测量的和模拟的控制点投影之间的平方距离之和,


最小化公式24的理由,当图像测量误差服从零均值各向同性高斯分布时,给出了摄像机参数的最大似然解。
透视相机
主要是如何计算P。非共面对象时,一个视角的数据就可以计算P,通过直接线性变换(DLT)方法计算(4.1.1节)。有了P,就可以分解K和R,再计算t。
另一种情况,共面特征时,需要多个视角的数据。首先K可以先确定,之后计算 R j \mathbf{R}_j Rj和 t j \mathbf{t}_j tj来初始化非线性优化。如果伴随畸变,畸变参数初始化为0。4.1.2详细描述,这个应该张正友的方法。
不共面的标定对象
通过叉乘消除未知尺度

上述方程对P的元素来说是线性的,可以变换为如下形式:

每个点对应提供了三个方程,但其中只有两个是线性独立的。那么,最少需要6个点,来解
A
v
=
0
\mathbf{A}\mathbf{v}=\mathbf{0}
Av=0方程。
A
\mathbf{A}
A是
A
i
\mathbf{A}^{i}
Ai堆叠得到的。由于测量误差不会得到精确的解。但是最小化
∥
A
v
∥
\left \| \mathbf{A}\mathbf{v} \right \|
∥Av∥,可以用
A
\mathbf{A}
A的奇异值分解。但是,如果点
X
i
\mathbf{X}^i
Xi是共面的,那么存在模糊解。因此DLT不适合用在共面特征的情况下。
DLT计算前,要对数据进行归一化操作,即零均值和单位方差。这样可以有效避免噪声对结果的影响。这种思想用在很多算法中,如kasch算法。
平面标定对象
这个在张正友的文献中有详细叙述。主要是解单应性矩阵

全向相机
这个过程分为三步:
-
内部参数初始化。根据一些先验知识初始化,

内参和畸变参数。 -
反投影和单应矩阵的计算。两步:投影到单位球;投影到像平面。
-
初始化外部参数,R和t
-
最小化重投影误差,LM算法求解
圆形控制点
为了实现精确的校准,我们使用了带有圆形控制点的校准平面,因为投影圆的质心可以以亚像素级的精度来检测[28]。然而,在这种情况下,问题是投影圆的质心不是原始圆中心的图像。当然,如果控制点真的是点状的,比如棋盘图案的角,这不是问题。
在透视相机的情况下,给定相机参数和校准平面上的圆,可以解析地求解投影圆的质心[1]。然而,在第3.2.3节的普通摄像机模型的情况下,投影更加复杂,投影圆的质心必须用数值方法求解[2]。
实验
镜头失真不严重的传统相机
实验表明 M 23 \mathcal{M}_{23} M23在所有情况下都表现不错,不管是传统相机还是鱼眼相机。但是对于窄角和宽角镜头,各模型间的差异不大。 M p M_p Mp模型对窄角镜头效果不错,但好像其他模型对广角模型更好。过拟合是通过增加图像数量解决。
鱼眼相机
然而,对于双曲线相机,M23中的附加自由度明显提高了校准精度。这可能表明摄像机的光轴没有与镜轴精确对准。然而,非对称中心相机模型M23也为这种反折射相机提供了良好的近似。同样,这里的中心模型似乎也适用于严格意义上的非中心等角折反射相机。请注意,鱼眼相机的分辨率不同于折反射相机。
M 23 \mathcal{M}_{23} M23是假设s=0时, M 24 \mathcal{M}_{24} M24的简化版本,见3.2.3节。
Geometric camera calibration using circular control points ↩︎






















 522
522











 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








