Path Integral Based Convolution and Pooling for Graph Neural Networks(PANConv)

Path Integral Based Convolution and Pooling for Graph Neural Networks(PANConv)

摘要

图神经网络将传统神经网络的功能扩展到图结构数据。与CNNs类似，图卷积和池化的优化设计是成功的关键。我们借鉴物理学的思想，提出了一种基于路径积分的图神经网络(PAN)，用于图上的分类和回归任务。具体来说，我们考虑了一个卷积操作，它涉及到每个连接消息发送者和接收者的路径，其权重取决于路径长度，这对应于最大熵随机游走。它将图拉普拉斯变换推广到一个新的转移矩阵，我们称之为最大熵转移(MET)矩阵，它是由路径积分形式导出的。重要的是，MET矩阵的对角线条目与子图的中心性直接相关，从而导致一种自然和自适应的池化机制。PAN提供了一个通用的框架，可以针对不同大小和结构的图形数据进行定制。我们可以将大多数现有的GNN架构视为PAN的特殊情况。实验结果表明，PAN在各种图分类/回归任务中都取得了一流的性能，包括一个来自统计力学的新基准数据集，我们建议促进GNN在物理科学中的应用。

1.引言

卷积神经网络(CNNs)的成功促使研究人员为图结构数据开发类似的架构。由于没有规则的网格，这项任务很有挑战性。一个值得注意的建议是在傅里叶空间中定义卷积[12,11]。该方法依赖于找到图拉普拉斯$I-D^{-1}A或I-D^{-1/2}A{D}^{-1/2}$的频谱，然后对输入信号X在相应基下的分量进行滤波器处理，其中A是图的邻接矩阵，D是对应的度矩阵。由于图拉普拉斯对角化的计算复杂度高，人们提出了许多简化方法[17,34]。

基于图拉普拉斯的方法本质上依赖于消息在直接连接的节点之间传递[27]，所有边共享相同的权值，这在本质上是在图上定义的通用随机游走(GRW)。这在GCN模型[34]中表现得最为明显，其归一化邻接矩阵直接应用于输入的左手边。在统计物理中，$D^{-1}A$被称为在图上做随机行走的粒子的转移矩阵，其中粒子以等概率跳到所有直接连接的节点。许多直接的基于空间的方法[28,40,54,63]可以被看作是GRW的一般化，但相邻方法的权重有偏差。

在本文中，我们超越了当路径分支时信息必然稀释的GRW图，而是将连接消息发送者和接收者的每一条路径视为消息传递中的基本单位。受Feynman提出的路径积分公式的启发[24,23]，我们提出了一种图卷积，根据每个路径的长度为其分配可训练的权重。该公式得到了一个极大熵跃迁(MET)矩阵，它与GRW中的图拉普拉斯变换相对应。通过引入一个虚构的温度，我们可以不断地调整我们的模型，从一个完全本地化的模型(MLP)到一个基于频谱的模型。重要的是，MET矩阵的对角线与子图的中心性密切相关，因此提供了一种不需要额外计算的自然池化方法。我们将这种基于完整路径积分的图神经网络框架称为PAN。

2. Path Integral Based Graph Convolution

Path integral and MET matrix

费曼路径积分公式[24,69]将概率振幅$\phi (x,t)$解释为位形空间中的加权平均值，其中${\phi }_0(x)$的贡献是通过对连接自身和$\phi (x,t)$的所有路径的影响求和(记为$e^{iS[x,\dot{x}]}$)来计算的。该公式后来被广泛应用于统计力学和随机过程[35]。我们注意到，这个公式本质上是通过考虑连续空间中所有可能路径的贡献来构建一个卷积。利用这个想法，但是修改离散图结构，我们可以启发式地提出一个统计力学模型，关于信息如何在给定图上的不同节点之间共享。在最一般的形式中，我们将具有$N$个节点的图的第$i$个节点的可观察对象${\phi }_i$写成

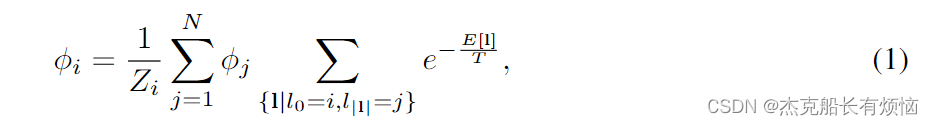
其中$Z_i$是标准化因子，即第$i$个节点的配分函数。这里路径$l$是连接节点的序列$(l_0{l}_1\dots l_{|l|})$，其中$A_{l_i{l}_{i+1}}=1$，路径长度用$|l|$表示。在图1中，我们在离散版本和原始公式之间进行了类比。很明显，积分现在应该被求和所取代，而${\phi }_0(x)$只存在于节点上。由于统计力学的观点在我们的情况下更合适，我们直接将指数项，它最初是拉格朗日的积分，改为一个虚构的能量$E[l]$和温度$T$的玻尔兹曼因子(我们选择玻尔兹曼常数$k_B=1$)。尽管如此，我们仍然利用了能量是路径的函数这一事实，这为我们提供了一种通过某一路径衡量其他节点影响的方法。虚构的温度控制着系统的激励水平，它反映了信息在多大程度上是局域的或扩展的。在实际操作中，不需要单独学习虚拟的温度或能量，神经网络可以直接学习整体权重，这在后面会更清楚地说明。

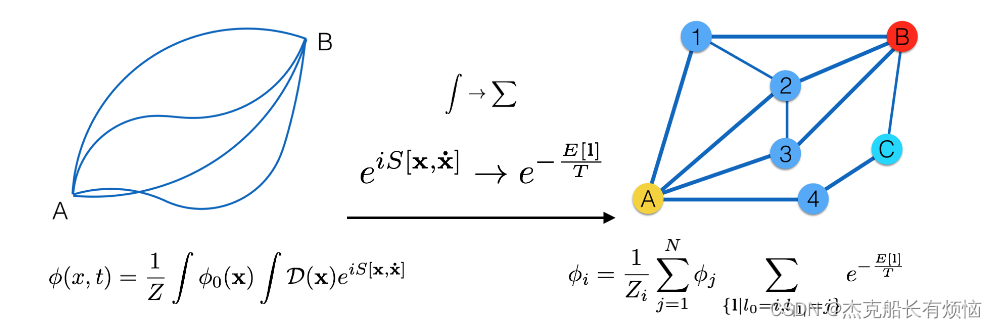
在连续空间中的原始路径积分公式(左)和图形的离散版本(右)之间的示意性类比。符号在文本中定义。

为了得到我们的模型的显式形式，我们现在引入一些温和的假设和简化。直观上，我们知道信息质量通常随着信息发送者和接收者之间的路径变长而衰减，因此我们可以合理地假设能量不仅是路径的函数，而且可以进一步简化为完全依赖于路径长度的函数。显然，在原则上，我们可以合并单个边的信息，比如用一个以路径上的节点为输入的神经网络来替代能量。因此，这里使用的常量形式应该只被理解为一般框架的最简单实现。在随机漫步图中，这种简化意味着在所有相同长度的路径中跳跃是等可能的，从而使路径的概率分布的Shannon熵在全局上最大化，因此将随机漫步命名为最大熵随机漫步[13]。2首先通过对路径长度的限制，我们可以引入第n层的总体权值$k(n;i)$为节点$i$如下

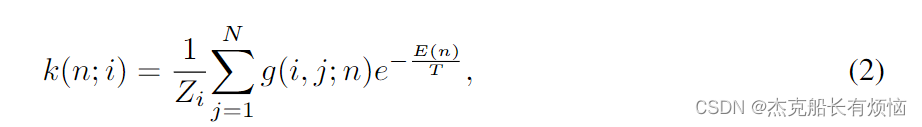
在$g(i,j;n)$表示长度为$n$的节点$i和j$之间的路径数，或$E(n)$能级关于节点$i和j$的状态密度，并对图中的所有节点求和。直观地说，节点$j的g(i,j;n)$表示与节点$i$通信的通道更多，因此可能与我们的公式一样对节点$i$的影响更大。例如，在图1中，节点B和C与A的距离都是两步，但是B连接A的路径更多，因此会被赋予更大的权重。可以推测，能量$E(n)$是$n$的递增函数，随着$n$的增加，会导致权重的衰减通过应用最大路径长度$L$的截断，我们交换(1)中的求和顺序，得到

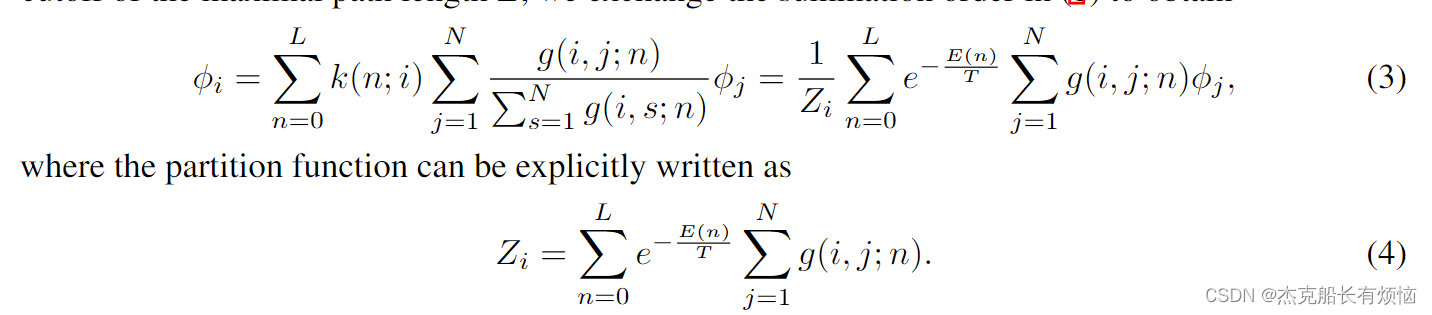
这种形式的一个很好的性质是我们可以很容易地计算$g(i,j;n)$将邻接矩阵A的幂提高到n，这是图论中邻接矩阵的一个众所周知的性质，即$g(i,j;n)=A_{ij}^n$。代入(3)，我们现在有一组由转移矩阵M(量子力学中传播子的对应项)控制的自洽方程，它可以写成以下紧致形式

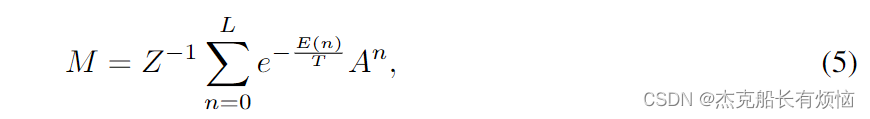
式中$diag(Z{)}_i=Z_i$。我们称该矩阵为$M$最大熵跃迁矩阵，因为它在微正则系综下实现了最大熵。在我们的框架下，这个转移矩阵取代了拉普拉斯变换的作用。

更一般地，我们可以将考虑到的路径约束为最短路径或自避免路径。必然地$g(i,j;n)$将采取更复杂的形式，矩阵$A^n$需要相应修改。在本文中，我们专注于最简单的场景，并且不应用任何约束来简化讨论。

PAN convolutionPAN

本征态，或者说系统$\psi i$满足$M{\psi }_i=\lambda {\psi }_i$。类似于由图拉普拉斯算子形成的基，我们可以根据MET矩阵的谱来定义图卷积，现在它有了明确的物理意义。然而，当M更新时，在每次迭代中对角化M在计算上是不切实际的。为了减少计算复杂度，我们应用类似于GCN[34]的技巧，直接将M乘到输入的左侧，并在右侧伴随另一个权值矩阵W。然后将卷积层简化为简单形式

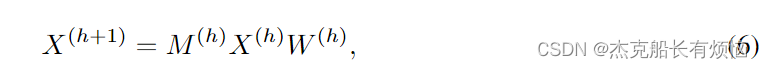
其中$h$为层数。将$M$应用于输入$X$实质上是给定节点的邻居之间的加权平均值，这导致了一个问题，即在数据驱动的环境中，是否与路径积分公式相一致的归一化最有效。实验一致表明，对称归一化通常会给出更好的结果[34,41,43]。这个观察结果可能有一个直观的解释。通常，可以考虑$Z^{-{\theta }_1}\cdot Z^{-{\theta }_2}$的归一化，其中${\theta }_1+{\theta }_2=1$。有两种极端的情况。当${\theta }_1=1和{\theta }_2=0$时，它被称为随机游走归一化，该模型可以理解为“接收器控制”，在这种意义上，感兴趣的节点在所有相邻节点之间按连接它们的信道数加权进行平均。相反，当${\theta }_1=0和{\theta }_2=1$时，模型变为“发送方控制”，因为权重是由从发送方流出的流向接收方的流量的比例决定的。因为对于无向图，连接节点之间的确切交互是未知的，作为一种折衷，对称归一化可以优于两个极端，即使它可能不是最优的。这一考虑导致我们最终的完善步骤，将$M$中的归一化$Z^{-1}$变为对称的归一化版本。卷积层就变成了

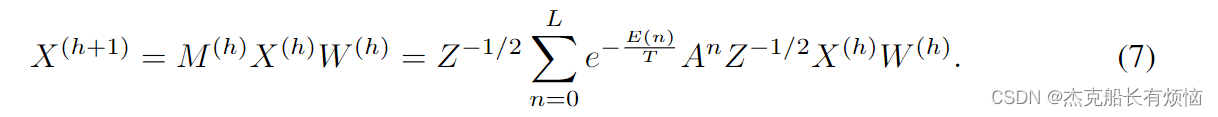
我们称这个图为PANConv。

级数的最佳截止点$L$取决于图的固有性质，它由温度$T$表示。包含更多的项就类似于在更高的温度下使更多的粒子被激发到更高的能级。例如，在低温极限L = 0时，将模型简化为MLP模型。在高温极限下，$exp(-E(n)/T)$各因子均为1，且幂次最大的项占主导。$A^n={\sum }_{i=1}^N{\lambda }_i^n{\psi }_i{\psi }_i^T$，其中${\lambda }_1，\dots ,{\lambda }_N$按降序排序。由Perron-Frobenius定理可知，当$n\to \infty$时，导阶项仅具有唯一的最大特征值${\lambda }_1$。然后，我们得到了高温模型$X^{(h+1)}=(I+{\psi }_1{\psi }_1^T)X^{(h)}{W}^{(h)}$的原型。截止点$L$的最合适选择反映了图的本征动力学。

3. Path Integral Based Graph Pooling

对于图分类和回归任务，另一个关键组件是池化机制，它使我们能够处理具有可变大小和结构的图输入。在这里，我们展示了PAN框架提供了一个基于MET矩阵的节点重要性的自然排序，它与子图的中心性密切相关。这种池化方案称为PANPool，它除了卷积之外不需要进一步的工作，可以自适应地发现潜在的局部母题。

MET matrix and subgraph centrality

在复杂网络社区中，人们提出了许多不同的方法来为图中节点的“重要性”排序。最直接的是程度中心性(DC)，它计算邻居的数量，其他更复杂的度量包括，例如，中间中心性(BC)和特征向量中心性(EC)[45]。尽管这些方法确实给出了节点全局重要性的具体度量，但它们通常无法选取局部模式。然而，从CNNs对图像分类的工作方式来看，我们知道，重要的是局部代表性像素。

Estrada和Rodriguez-Velazquez[21]的研究表明，子图中心性在检测局部图形基序方面优于上述方法，这对于许多社会和生物网络的分析至关重要。子图中心性计算不同长度的自环数的加权和。在数学上，对于节点$i$它简单地写为${\sum }_{k=0}^{\infty }(A^k{)}_{ii}/k!$有趣的是，人们马上就能看到这个表达式和MET矩阵的对角线元素的相似之处。这种差异很容易解释。MET矩阵中的和在最大长度$L$处被截断，不同路径长度$e^{\frac{E(n)}{T}}$的权值是可学习的。相比之下，预定的权重为$1/k!$为保证求和的收敛性，给出了结果的解析形式:${\sum }_{j=1}^N{v}_j^2(i)e^{{\lambda }_j}$，其中$v_j(i)$为与特征值${\lambda }_j$相关的标准正交基的第$i$个元素。

现在我们可以清楚地看到，MET矩阵不仅扮演了基于路径积分的卷积的角色，它的对角线元素Mii也自动提供了节点i重要性的度量，从而通过对Mii进行排序实现了池化机制。重要的是，与子图中心性相比，这种池化方法有三个主要优点。首先，我们可以利用易于计算的MET矩阵，从而避免额外的计算，特别是在子图中心性的情况下，邻接矩阵的直接对角化。其次，权重是数据驱动的，而不是预先确定的，可以有效地适应不同的输入。此外，MET矩阵被规范化(注意，与卷积的情况不同，这里的规范化是否对称并不重要。对于池化，我们只关心对角线项，不同的归一化方法会给出相同的结果。)，这增加了节点的局部重要性的权重，并可能避免在现实世界的“无标度”网络中常见的围绕“枢纽”聚类[8]

PAN池策略与PAN卷积有相似的物理解释。以低温极限为例，当截断值设为L = 2时，${\sum }_{n=0}^L{e}^{\frac{E(n)}{T}}{A}_{ii}^n$的阶数与阶数相同，从而恢复了阶数的中心性。在高温极限下，当$n\to \infty$时，和由与A的最大特征值相关的标准正交基第$i$个元素的大小决定，因此相应的排序简化为特征向量中心性排序。通过调优$L$, PANPool提供了一种灵活的策略，可以适应输入的“甜点”。

为了更好地理解提出的方法的效果，在图2中，我们通过对称为RSA的连接点模式的节点重要性的不同度量来可视化前20%的节点，我们在第5.2节中详细介绍。值得注意的是，直流电选点相对均匀，而EC选点结果高度集中。这一现象类似于经典图中相当均匀的扩散与无序系统[13]中量子力学中的安德森定域[5]之间的对比。在这个意义上，它试图找到最适合输入数据结构的“介观”描述。重要的是，我们注意到，非标准化的MET矩阵往往集中在密集连接的区域或中心。相比之下，标准化的节点倾向于选择局部代表性节点，而忽略中心节点中同样良好连接的节点。根据这一观察结果，我们提出了一种改进的池策略，该策略可以平衡全部和局部级别的影响。

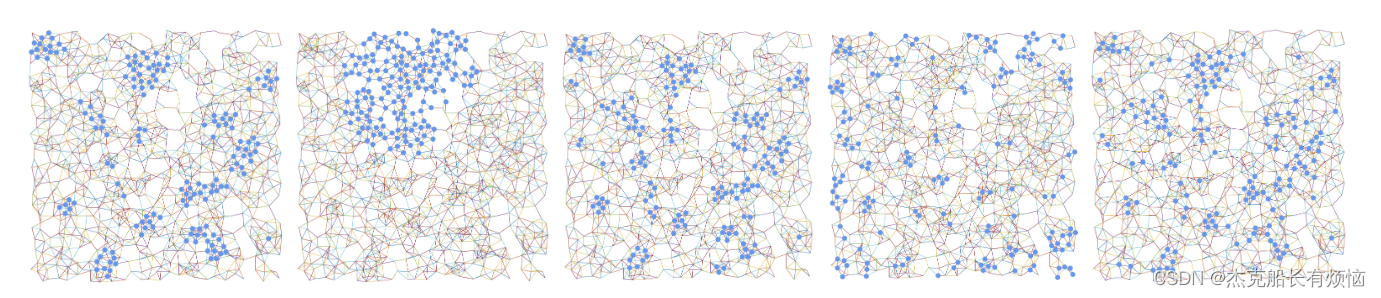
根据PointPattern数据集中RSA模式节点重要性的不同度量，前20%的节点(用蓝色表示)。从左到右分别是:度中心性、特征向量中心性、未归一化的MET矩阵、MET矩阵和混合PANPool。

Hybrid PANPool

为了结合局部主题的贡献和全局的重要性，我们建议使用一个简单的线性模型混合PAN池(仍然被称为PANPool)。全局重要性可以用输入信号X本身的强度来表示，但不限于此。更精确地说，我们用一个可训练的参数向量$p\in R^d$投影特征$X\in R^{N\times d}$，并将其与MET矩阵的对角线对角线(M)结合，得到一个分数向量。

在这里$\beta$是一个真正的可学习参数，控制这两个潜在竞争因素的重点。然后PANPool选择由该分数排序的节点中的一部分(由K表示)，输出池中的特征数$\tilde{X}\in R^{K\times d}$和对应的邻接矩$\tilde{A}\in R^{K\times K}$。这个新的节点评分(8)联合考虑了节点特征(全局层面)和图结构(局部层面)。在图2中，PANPool倾向于选择在本地和全局都很重要的节点。在同样的考虑下，我们也测试了其他的设计方案，详见补充资料。

4. 相关工作

图神经网络最近受到了广泛关注[9,40,51,60,67,68]。对于图的卷积，许多工作都考虑了空间域的一阶邻接矩阵或谱域的图拉普拉斯变换。Bruna等人[12]首先提出了使用傅里叶方法的图卷积，然而，这是计算昂贵的。人们提出了许多不同的方法来克服这个困难[6,15,16,17,27,29,34,44,52,61,62]。另一个关键流考虑[54]注意机制，该机制无需使用扩散图就可以推断节点之间的相互作用。还有一些GNN模型使用多尺度信息和高阶邻接矩阵[1,2,3,25,36,41,59]。与一般的扩散图[28,48,53]相比，最大熵随机游走在链路预测[39]或社团检测[47]任务上已经表现出了优异的性能。然而，许多流行的模型可以与我们的框架相关，或者被视为特定的显式实现。我们可以将MET矩阵解释为作用于图输入的一个操作符，它作为一个内核，在给定节点的邻居之间分配适当的权值。这种机制类似于[54]的注意机制，但我们基于物理直观限制了MET矩阵的函数形式，并保持紧致形式。虽然我们通过应用MET矩阵保持特性数量不变，但我们可以很容易地将近邻的聚合信息连接起来，比如GraphSAGE[29]或GAT[54]。重要的是，截断L的最佳选择揭示了图的内在动态特性。特别地，选择L = 1，模型(7)本质上就是GCN模型[34]。通过将(7)中的A替换为$D^{-1}A或D^{-1/2}A{D}^{-1/2}$，我们可以很容易地将模型转换为多步GRW版本，这确实是LanczosNet[41]的格式。关于PAN卷积的初步想法已经在之前的ICML研讨会[43]上提出，PAN卷积的有效性已经通过其在节点分类任务上的卓越性能得到了证明。本文提出了一个基于路径积分的卷积和池化机制的完整框架，重点讨论了图级的分类和回归任务。

图池化是gnn的另一个重要组成部分，用于使图分类和回归任务的输出大小一致。研究者们从不同的角度提出了很多pooling的方法。例如，可以只考虑节点特征或节点嵌入[20,27,55,66]。这些全局池化方法没有利用图的层次结构。增强学习能力的一种方法是建立一个具有可训练操作或参数的数据依赖池化层[14,26,37,38,64]。在图池化中可以包含更多的边信息[18,65]。我们也可以使用光谱方法，在傅里叶或小波域进行池[42,46,57]。PANPool是一种同时考虑特性和结构的方法。最后，它没有逃脱我们的分析，路径的损失可能是一种有效的方法，以实现辍学。最后，由于PAN可以通过寻找最优L来学习图的内在动态的最优表示，因此PAN有可能缓解消息传递gnn[4]的公共信息瓶颈。一个相关的有趣的理论问题可能是比较一个非常“宽”的PAN和一个深度的GCN。

5. 实验

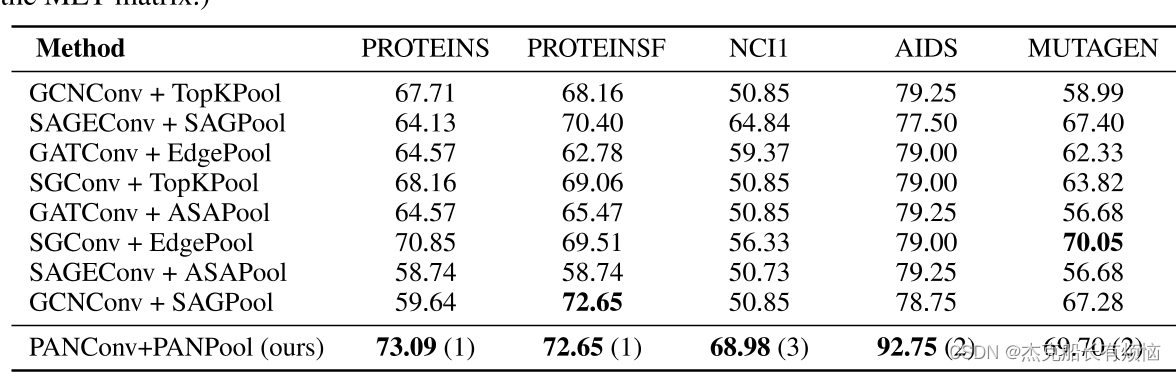
图分类任务的性能比较(测试准确率百分比;粗体用于突出显示列表中表现最好的内容;括号中的值是MET矩阵中使用的截止$L$。

从左到右:PointPattern数据集中从HD、泊松和RSA点处理生成的图样本。

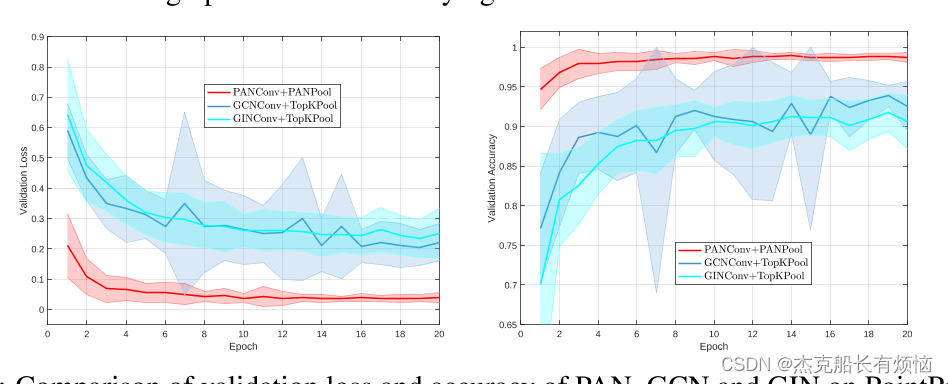
相似网络架构下，10次重复，比较PAN、GCN和GIN在PointPattern上的验证损失和准确性。

PAN, GIN和GCN在三种不同难度的PointPattern数据集上的测试精度(百分比)，epoch高达20。括号中的值是L的截止值。