模糊表示学习笔记

umbrellazg

于 2025-04-13 11:37:40 发布

阅读量934

点赞数 21

文章标签：学习笔记

本文链接：https://blog.csdn.net/m0_51576139/article/details/142101086

版权

图表示学习通常从图的拓扑结构和高维节点属性中产生低维和清晰的表示。然而，节点或图的清晰表示实际上隐藏了特征的不确定性和可解释性。例如，在引文网络中，两篇论文之间的引用总是涉及表示相关度的future，也就是说，一个连接可能同时属于不同belief中的强引用和弱引用。

本文首次提出了一种无监督的图和网络模糊表示学习模型，通过使清晰的表示模糊化来提高它们的表达能力。具体来说，本文提出了一种模糊图卷积神经网络（FGCNN），它可以聚合高级模糊特征，利用模糊逻辑充分挖掘特征级的不确定性，最终生成模糊表示，相应的由多个FGCNN组成的层次模型，称为深度模糊图卷积神经网络（DFGCNN）

先验知识：

1、隶属度：隶属度是一个介于0和1之间的数值，用来表示一个元素属于某个模糊集合的程度。
2、隶属函数是定义隶属度的函数，它根据输入值的不同，输出一个介于0和1之间的数值。常见的隶属函数形状包括：三角形隶属函数：具有三个参数（通常表示为顶点和两个基点），形状像一个三角形。高斯隶属函数：基于高斯分布（也称为正态分布），形状像一个钟形曲线。梯形隶属函数：具有四个参数（通常表示为两个对角的基点），形状像一个梯形。
3、“信念程度”通常指的是一个元素属于某个模糊集合的隶属度。这个概念用来描述一个特定值与模糊集合之间的关系强度。

模糊逻辑系统的架构：

Fuzzifier:模糊化器将一个精确值映射为具有隶属函数的模糊数，该隶属函数产生一个隶属度，用以衡量这个精确值属于某个特定模糊集的信念程度。这种从精确域到模糊域的转换是根据隶属函数进行的。三角形、高斯形和梯形隶属函数是最常用的。
Rule base:规则库是模糊逻辑系统（FLS）的核心。这些规则通常由领域专家提供，或者通过模糊神经网络（FNN）从大量数据中自动提取。它利用“if-then”规则来模拟特征之间的关系，其中“if”部分称为前件，而“then”部分称为后件。

Inference engine:推理引擎根据一些代数运算对模糊集合和规则进行操作，包括并集、交集和补集。假设有两个不同的模糊集 F1 和 F2，由两个模糊成员函数 μF1 和 μF2 定义，这些操作可以表示为

规则中的蕴涵运算符由交集运算符计算，以便将前件和后件结合起来

Output processor:输出处理器将模糊集合中的模糊结果转换为精确输出，这个过程称为去模糊化。去模糊化的目的是全面考虑适当的条件，以达成最终的共识。有许多去模糊化方法，例如，集的中心法，其公式为：其中，K 是“if-then”规则的数量，fk 表示第 k 条规则的激活水平，ckc 表示第 k 个模糊集合的质心。假设模糊表示具有更强的表现力，本文选择避免进行去模糊化处理，因为这个过程会在一定程度上减少不确定性。同时，模糊集合的结果可能会引入更多的参数，从而增加模型的复杂性。

PROPOSED MODEL：

1、问题定义：目标是训练一个模糊图编码器 F以嵌入原始属性和结构，然后产生低维模糊节点表。这样的表示具有完成各种下游任务的能力，如节点分类、链接预测和社区检测。

2、图对比学习框架：对比模型需要准确地选择正对和负对，因为对比学习追求的是正对具有相似的表示，而负对具有不同的表示。为了避免崩溃，对比学习需要大量的负对。图增强通常用于选择用于对比的负样本，而所选的负样本对最终的表示有很大的影响力。本文提出的 DFGCNN 继承了一种流行的图对比框架，该框架旨在保持原始图的两个视图之间的一致性。

在GRACE框架中训练的DFGCNN（深度图卷积神经网络）首先根据两种不同的图增强τ1和τ2生成两个不同的图视图。这两个视图随后被输入到DFGCNN中，得到各自的模糊表示矩阵H1和H2。最后，计算这两个模糊表示矩阵之间的对比损失。
3、模型结构：FGCNN包括聚合过程和模糊化过程。聚合过程用于抽象和聚合高级特征，模糊化过程用于处理图的不确定性和特征的可解释性。

DFGCNN在模糊化之前先对原始输入进行特征的聚合和抽象。模糊化特征会显著增加与特征维度相关的参数数量。因此，如果先对初始属性进行模糊化，将会给计算效率带来沉重负担，并使模型容易过拟合。此外，GCN通过降维来避免直接处理高维数据，这是模糊逻辑的主要缺陷。考虑到这些，本文决定通过预先的聚合过程从原始属性矩阵X中压缩节点特征，该过程由下式给出：

其中，表示经过归一化的邻接矩阵；是第(l − 1) 层 DFGCNN 的输出，表示可训练的权重矩阵；是聚合过程的输出隐藏特征矩阵。与传统GCN中的聚合过程不同，DFGCNN中的聚合过程不以ReLU或PReLU等非线性激活函数结束，因为模糊化过程实际上提供了足够的非线性特性。
模糊化过程是 FGCNN 的核心，其细节如图所示，包括模糊化算子和组合算子。基于模糊集理论，模糊化算子能够从清晰的特征元素中产生模糊性，而组合算子则用于提取重要的模糊信息。

在第 (l) 层的模糊图卷积神经网络（FGCNN）中，首先对第 (l-1) 层的高级特征进行聚合和抽象。然后，使用高斯隶属函数计算不同的隶属度。每个隶属度都表示特征向量中的元素 h_{i,j}属于某个模糊集的程度。接下来，通过施加最大操作符来选择与 h_{i,j}最可能所属的模糊集对应的最大隶属度。这个操作被视为从不同模糊集中选择最显著的模糊信息。为了融合原始特征和模糊性，应用了哈达玛积

现在将从第 l 个 FGCNN 的聚合过程中抽象出来的节点 v_i 的隐藏特征向量表示为。为了模糊化以获得高级模糊摘要，该特征通过一系列成员函数转换为模糊特征空间,其中，为计算出的的隶属度，表示特征向量的第 j 个元素。经过此变换后，每个元素都开始具有模糊性，表示属于某个模糊集的程度。表示隶属函数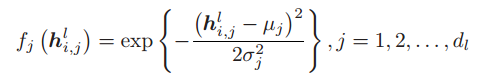，，其中，高斯隶属函数的平均值 μj 和标准差 σj 被视为可训练参数。为了加速学习过程，利用 K-means 等聚类算法为所有高斯隶属函数初始化这些参数。适当增加隶属函数的数量可以产生更多的模糊性，增强模型的表达能力。为了使每个元素具有足够的表达能力，为每个元素设置F个高斯隶属函数。每个隶属函数对应一个特定的模糊集，该模糊集对应于一个有意义的属性，即为了从不同的模糊集中提取最重要的模糊信息，采用最大算子，定义为
其中被认为是最重要的模糊信息。合并模糊信息和特征信息的一个简单方法是计算

其中，为原始特征信息与模糊信息的融合导数，同样为节点的期望模糊向量；为Hadamard 积，该融合算子也视为信息补集。由于隶属函数的作用，特征向量的所有元素被压缩到[0, 1] 区间，从而丢失了部分特征信息，限制了特征在各个维度上都表现出显著性。

此外，由于每个隐藏的特征向量都被转换为模糊特征空间，因此后续的 FGCNN 能够从邻居那里聚集越来越多的模糊性。堆叠更多 FGCNN 会产生一个深度模型，称为 DFGCNN。当当前层数 l 大于 1 时，模糊表示矩阵的计算如下：

其中是第 l 个模糊化过程生成的模糊特征矩阵，是第 (l + 1) 个 FGCNN 的聚合过程的输出，是第 (l + 1) 个 FGCNN 中的隶属度矩阵。为简单起见，表示为模糊编码器 F 的最终输出，与层数无关，表示为的最终模糊表示。

损失函数：以区分两个全等图视图中的同一节点与其他节点。定义一个由 ER 【Edge Rewiring】和 FM【Feature Masking】操作组成的图数据增强操作集 T，在每个训练阶段，都会将两个数据增强算子 τ1、τ2 ∈ T 应用于输入图以获得两个不同的视图 G1 = τ1(G) 和 G2 = τ2(G)。如上图所示，vi 和它在另一视角对应的节点 ui 被视为唯一的正节点对，用蓝色箭头表示。vi 和两个视角中的其他节点为负节点对，用紫色和红色点箭头表示。正节点对 (vi, ui) 的损失函数定义为