匈牙利匹配算法

一 什么是匈牙利匹配算法

匈牙利匹配（Hungarian Algorithm），也称为最小成本匹配或科奇-劳斯算法，是一种经典的线性规划方法，用于解决一种特殊的配对问题，即在一个二维的成本矩阵中，找到一种配对方式使得总的匹配成本最小，同时保证每个元素都恰好被匹配一次。这个问题通常出现在任务分配、员工排班等需要优化资源分配的情况中。
算法的核心思想是通过逐步构建一个分配表，通过一系列的交换操作将成本矩阵转化为一个“完全匹配”的状态，即每个行和列都只有一个非零元素。这个过程利用了所谓的“循环取消”技术，通过比较当前分配与最优分配的差异，找到一个交换可以最小化总成本。

二 一个关于匈牙利算法的例子

假设有如下一个实际问题。这里有n份工作任务，有n个工人，每个工人完成工作所需的成本不同（可以时间成本，可以是经济成本），但是由于每个工人在同一时间只能做一个工作，每个工作因此只能分配给一个工人，需要给出一个算法，求出总的花费成本最低。

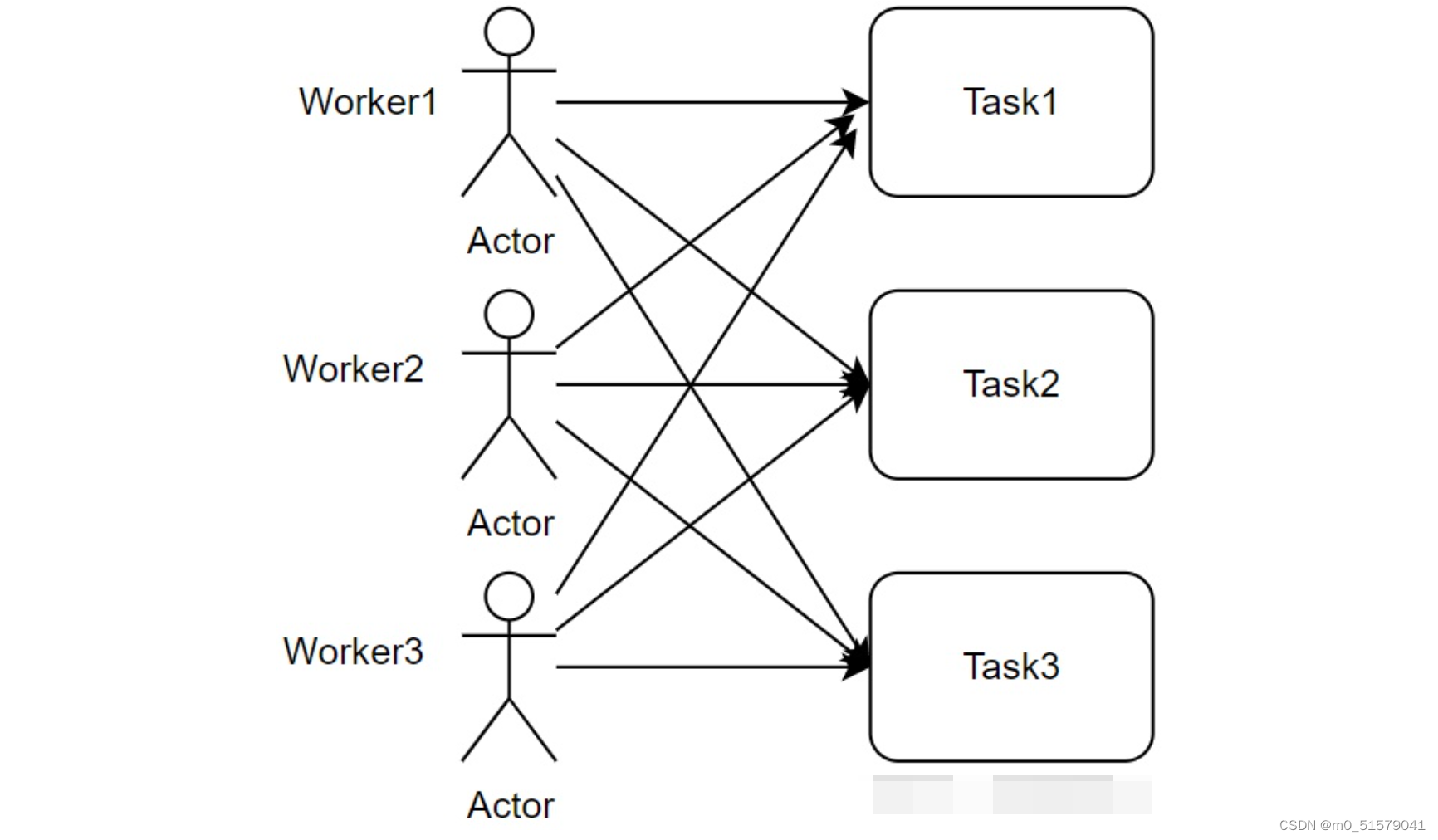
下面介绍其实现流程：

（1）创建cost matrix

那么上面这个表格或者说是矩阵，的第(i,j)个元素的值就对应着第i个工人分配给他