1、 “锚框”生成说明
step1 背景是一张图片,在图片中密集的黑色点点就是按照定步长确定的”锚点“
step2 在每个锚点处,都会生成三种尺寸的正方形的框(红色、绿色、蓝色中的正方形框)
step3 对每个正方形框,会生成两种扩展尺度的框(每种颜色的另外两个长方形)
step4 所以,在每个锚点处都会生成9个anchor
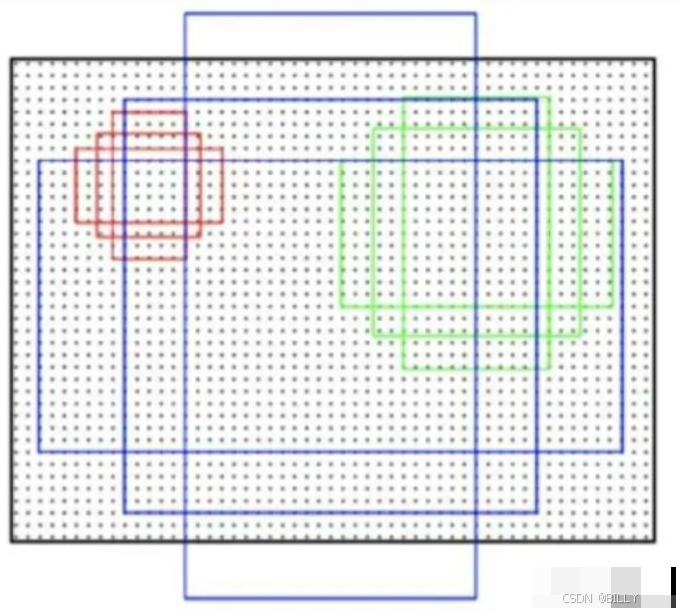

Anchor的生成过程和深度学习没有任何的关系,他的本质只是你设定好一些规则,并依据这些规则,在图像中生成不同尺寸,不同长宽比的框,并希望这些框能够最终覆盖你的物体。
Anchor base的缺点
-
检测表现效果对于锚框的尺寸、长宽比、数目非常敏感,因此锚框相关的超参数需要仔细的调节。
-
锚框的尺寸和长宽比是固定的,因此,检测器在处理形变较大的候选对象时比较困难,尤其是对于小目标。预先定义的锚框还限制了检测器的泛化能力,因为,它们需要针对不同对象大小或长宽比进行设计。
-
为了提高召回率,需要在图像上放置密集的锚框。而这些锚框大多数属于负样本,这样造成了正负样本之间的不均衡。
-
大量的锚框增加了在计算交并比时计算量和内存占用。
2、 以Faster RCNN为例说明
2.1 Faster RCNN中的anchor的得出原理是什么?
固定的,长宽比为:0.5;1;2,尺度为:8;16;32
其实从源码上看,可分为两个步骤:
1)保持anchor的面积不变,但是改变长宽的比例。此步有三个比例,最终得到三个不同长宽比的预测框
2):保持长宽的比例不变,但是进行scale的缩放,从而改变比例。此步是在上一步的基础上进行的,也是有三个比例,将每一个长宽比的预测框,缩放三次,那么最后,就得到了9个预测框=
2.2 Faster RCNN中给定一张图如何计算anchor的数量?

以源码为例,源码初始坐标为[0, 0, 15, 15]意味着第一个anchors对应的预测框的左上角坐标为(0,0),右下角的坐标为(15,15)。那么这个框移动的时候,以边长为步长,覆盖过的区域就不再覆盖了,所以,可以断步长为16(应知计算机里面是从0就开始计数的,0到15,是一共16)那么,给定一个输入图片,可以产生多少个预测框呢?假设给定一个600800的大小的图片,那么先计算可移动的覆盖次数即:(800/16)(600/16)=1900,那么,每次覆盖产生9个anchors,则最终的结果是1900*9=17100,一共17100个anchor.对应效果如上图右边。
2.3 如何改变Faster RCNN中anchor的数量和尺寸?
还是要对应源码来解释的,Faster R-CNN源码产生anchors的部分,位置Faster
RCNN/lib/rpn/generate_anchors.py:
def generate_anchors(base_size=16, ratios=[0.5, 1, 2],
scales=2 ** np.arange(3, 6)):
从这里可以看出ratios的设定决定了产生的anchors的长宽比,scales设定决定了产生的anchosr的放缩尺度,anchors产生的个数是由这俩个设定的个数的乘积决定的,要是想改变个数就改变scales、ratios的参数个数即可。
3、 以YOLO为例说明
3.1 YOLO中的anchor的得出原理是什么?
首先设置anchor的目的是为了使得预测框与ground truth的IOU更好(这个就好比是中心思想,一切操作的源头,一定记着)
那么是怎么实现的呢?YOLO(准确的说是v2和v3的版本)的anchor机制是借鉴Faster RCNN的RPN来设定的,但又稍有不同,YOLO中的anchor的数量不像是RPN那样提前人工设置好的,而是,根据所检测的数据集的情况通过用K-means++算法通过聚类的方式得出来的。那么这里有个问题,就是明明中心思想是为了使预测框和GT的IOU更好,为啥和anchor的数量有关系呢?这就要解释anchor的机制,在RPN中,anchor的数量是由scales、ratios两个参数共同的乘积决定的(具体见上问),其中ratios就代表着长宽比,那么,引用到YOLO里面来,为了让预测框和TGT有更好的IOU,就需要对ratios这个参数进行设置,使得使用的anchor的预测框的尺寸跟最多的GT尺寸保持一种“天然”重合的趋势,即让开始的时候就把anchor的预测框形状设置成训练数据中最普遍的GT长宽比的大小,这样得出来的结果不就可以有更好的IOU了吗?那么,就对ratios进行设置,那么怎么设置呢?总不能像RPN那样提前规定好一个固定的长宽比进行设定吧,不同的训练集有不同分布的GT长宽分布,不能要针对不同对象选取不同的对策,故而,采用了用聚类的方式,找出所训练数据集中最普遍的长宽比,继而,用这个长宽比来作为anchor预测框的长宽比。那么在YOLO中,并没有关于scales缩放的操作,只是调整了长宽比,假设最后得出了n组长宽比,那么最后,决定的每个anchor对应的预测框数量就是n*1(scales认为是1)个了,那么大神们嘴里说的5个anchor指的就是再yolov2版本的时候,人家是用COCO数据集来作为训练集,那么对这个数据集通过聚类聚出了5个聚类中心,即有5个可以涵盖整个数据集框分布的最常见长宽比,那么对应的,就是所谓的“5”了。
PS:因为加入了anchor机制,v2可以预测的框的数量变为了(1313num_anchors)相比于v1中的(772),YOLOv2的召回率大大提升,由原来的81%升至88%。
下面通过代码记下anchor的是怎么通过聚类得到这个“5”的。
下面这个是个总的函数,用来执行k-means++的聚类,思路很简单,先把数据集给读进去,然后,把数据集里的所有的框,给放到一个集合里面,然后,从集合里面初始化一个最开始的聚类中心,然后,根据这个中心,反复的进行迭代,将离它最近的(这个距离的测量是根据计算IOU来代替的)框的长宽,累加起来再求平均,就是下一次迭代的聚类中心了,反复n(自己可设定)轮,直到迭代轮数停止,或等到计算的聚类中心满足了所设定的IOU距离,就停止,那么,剩下的距离中心,就是这个数据集所得的anchor的长宽比了。
# 计算给定bounding boxes的n_anchors数量的centroids
# label_path是训练集列表文件地址
# n_anchors 是anchors的数量
# loss_convergence是允许的loss的最小变化值
# grid_size * grid_size 是栅格数量
# iterations_num是最大迭代次数
# plus = 1时启用k means ++ 初始化centroids
def compute_centroids(label_path,n_anchors,loss_convergence,grid_size,iterations_num,plus):
boxes = []
label_files = []
f = open(label_path)
for line in f:
label_path = line.rstrip().replace('images', 'labels')
label_path = label_path.replace('JPEGImages', 'labels')
label_path = label_path.replace('.jpg', '.txt')
label_path = label_path.replace('.JPEG', '.txt')
label_files.append(label_path)
f.close()
for label_file in label_files:
f = open(label_file)
for line in f:
temp = line.strip().split(" ")
if len(temp) > 1:
boxes.append(Box(0, 0, float(temp[3]), float(temp[4])))
if plus:
centroids = init_centroids(boxes, n_anchors)
else:
centroid_indices = np.random.choice(len(boxes), n_anchors)
centroids = []
for centroid_index in centroid_indices:
centroids.append(boxes[centroid_index])
# iterate k-means
centroids, groups, old_loss = do_kmeans(n_anchors, boxes, centroids)
iterations = 1
while (True):
centroids, groups, loss = do_kmeans(n_anchors, boxes, centroids)
iterations = iterations + 1
print("loss = %f" % loss)
if abs(old_loss - loss) < loss_convergence or iterations > iterations_num:
break
old_loss = loss
for centroid in centroids:
print(centroid.w * grid_size, centroid.h * grid_size)
# print result
for centroid in centroids:
print("k-means result:\n")
print(centroid.w * grid_size, centroid.h * grid_size)
下面这部分是计算初始化的聚类中心的,先是随机的选一个框来作为初始化的框,centroid_index=np.random.choice(boxes_num, 1);然后,计算所有框到这个框的距离,并累加起来,将累加起来的值,乘上一个(0,1)之间的随机数,变成一个阈值,distance_thresh = sum_distance*np.random.random(),然后,再把刚刚的所有框都遍历一遍,如果大于这个阈值就认为下一个聚类中心点的聚类中心就是它了(这个过程中,所求的聚类中心的数量是需要提前设定好的,),这也是本着K-Means++算法在聚类中心的初始化过程中的基本原则是使得初始的聚类中心之间的相互距离尽可能远来进行,最后那个随机数选阈值的思路,学名叫做:以概率选择距离最大的样本作为新的聚类中心。
# 使用k-means ++ 初始化 centroids,减少随机初始化的centroids对最终结果的影响
# boxes是所有bounding boxes的Box对象列表
# n_anchors是k-means的k值
# 返回值centroids 是初始化的n_anchors个centroid
def init_centroids(boxes,n_anchors):
centroids = []
boxes_num = len(boxes)
centroid_index = np.random.choice(boxes_num, 1)
centroids.append(boxes[centroid_index])
print(centroids[0].w,centroids[0].h)
for centroid_index in range(0,n_anchors-1):
sum_distance = 0
distance_thresh = 0
distance_list = []
cur_sum = 0
for box in boxes:
min_distance = 1
for centroid_i, centroid in enumerate(centroids):
distance = (1 - box_iou(box, centroid))
if distance < min_distance:
min_distance = distance
sum_distance += min_distance
distance_list.append(min_distance)
distance_thresh = sum_distance*np.random.random()
for i in range(0,boxes_num):
cur_sum += distance_list[i]
if cur_sum > distance_thresh:
centroids.append(boxes[i])
print(boxes[i].w, boxes[i].h)
break
return centroids
最后,就是通过迭代来选取新的聚类中心的过程了,思路也是一样,计算最小距离,并记录下来,然后,把这些进行累加new_centroids[i].w /= len(groups[i]) new_centroids[i].h /= len(groups[i],再平均求和,就是新聚类中心的w和h了。
# 进行 k-means 计算新的centroids
# boxes是所有bounding boxes的Box对象列表
# n_anchors是k-means的k值
# centroids是所有簇的中心
# 返回值new_centroids 是计算出的新簇中心
# 返回值groups是n_anchors个簇包含的boxes的列表
# 返回值loss是所有box距离所属的最近的centroid的距离的和
def do_kmeans(n_anchors, boxes, centroids):
loss = 0
groups = []
new_centroids = []
for i in range(n_anchors):
groups.append([])
new_centroids.append(Box(0, 0, 0, 0))
for box in boxes:
min_distance = 1
group_index = 0
for centroid_index, centroid in enumerate(centroids):
distance = (1 - box_iou(box, centroid))
if distance < min_distance:
min_distance = distance
group_index = centroid_index
groups[group_index].append(box)
loss += min_distance
new_centroids[group_index].w += box.w
new_centroids[group_index].h += box.h
for i in range(n_anchors):
new_centroids[i].w /= len(groups[i])
new_centroids[i].h /= len(groups[i])
return new_centroids, groups, loss
完整代码
# coding=utf-8
# k-means ++ for YOLOv2 anchors
# 通过k-means ++ 算法获取YOLOv2需要的anchors的尺寸
import numpy as np
# 定义Box类,描述bounding box的坐标
class Box():
def __init__(self, x, y, w, h):
self.x = x
self.y = y
self.w = w
self.h = h
# 计算两个box在某个轴上的重叠部分
# x1是box1的中心在该轴上的坐标
# len1是box1在该轴上的长度
# x2是box2的中心在该轴上的坐标
# len2是box2在该轴上的长度
# 返回值是该轴上重叠的长度
def overlap(x1, len1, x2, len2):
len1_half = len1 / 2
len2_half = len2 / 2
left = max(x1 - len1_half, x2 - len2_half)
right = min(x1 + len1_half, x2 + len2_half)
return right - left
# 计算box a 和box b 的交集面积
# a和b都是Box类型实例
# 返回值area是box a 和box b 的交集面积
def box_intersection(a, b):
w = overlap(a.x, a.w, b.x, b.w)
h = overlap(a.y, a.h, b.y, b.h)
if w < 0 or h < 0:
return 0
area = w * h
return area
# 计算 box a 和 box b 的并集面积
# a和b都是Box类型实例
# 返回值u是box a 和box b 的并集面积
def box_union(a, b):
i = box_intersection(a, b)
u = a.w * a.h + b.w * b.h - i
return u
# 计算 box a 和 box b 的 iou
# a和b都是Box类型实例
# 返回值是box a 和box b 的iou
def box_iou(a, b):
return box_intersection(a, b) / box_union(a, b)
# 使用k-means ++ 初始化 centroids,减少随机初始化的centroids对最终结果的影响
# boxes是所有bounding boxes的Box对象列表
# n_anchors是k-means的k值
# 返回值centroids 是初始化的n_anchors个centroid
def init_centroids(boxes,n_anchors):
centroids = []
boxes_num = len(boxes)
centroid_index = np.random.choice(boxes_num, 1)
centroids.append(boxes[centroid_index])
print(centroids[0].w,centroids[0].h)
for centroid_index in range(0,n_anchors-1):
sum_distance = 0
distance_thresh = 0
distance_list = []
cur_sum = 0
for box in boxes:
min_distance = 1
for centroid_i, centroid in enumerate(centroids):
distance = (1 - box_iou(box, centroid))
if distance < min_distance:
min_distance = distance
sum_distance += min_distance
distance_list.append(min_distance)
distance_thresh = sum_distance*np.random.random()
for i in range(0,boxes_num):
cur_sum += distance_list[i]
if cur_sum > distance_thresh:
centroids.append(boxes[i])
print(boxes[i].w, boxes[i].h)
break
return centroids
# 进行 k-means 计算新的centroids
# boxes是所有bounding boxes的Box对象列表
# n_anchors是k-means的k值
# centroids是所有簇的中心
# 返回值new_centroids 是计算出的新簇中心
# 返回值groups是n_anchors个簇包含的boxes的列表
# 返回值loss是所有box距离所属的最近的centroid的距离的和
def do_kmeans(n_anchors, boxes, centroids):
loss = 0
groups = []
new_centroids = []
for i in range(n_anchors):
groups.append([])
new_centroids.append(Box(0, 0, 0, 0))
for box in boxes:
min_distance = 1
group_index = 0
for centroid_index, centroid in enumerate(centroids):
distance = (1 - box_iou(box, centroid))
if distance < min_distance:
min_distance = distance
group_index = centroid_index
groups[group_index].append(box)
loss += min_distance
new_centroids[group_index].w += box.w
new_centroids[group_index].h += box.h
for i in range(n_anchors):
new_centroids[i].w /= len(groups[i])
new_centroids[i].h /= len(groups[i])
return new_centroids, groups, loss
# 计算给定bounding boxes的n_anchors数量的centroids
# label_path是训练集列表文件地址
# n_anchors 是anchors的数量
# loss_convergence是允许的loss的最小变化值
# grid_size * grid_size 是栅格数量
# iterations_num是最大迭代次数
# plus = 1时启用k means ++ 初始化centroids
def compute_centroids(label_path,n_anchors,loss_convergence,grid_size,iterations_num,plus):
boxes = []
label_files = []
f = open(label_path)
for line in f:
label_path = line.rstrip().replace('images', 'labels')
label_path = label_path.replace('JPEGImages', 'labels')
label_path = label_path.replace('.jpg', '.txt')
label_path = label_path.replace('.JPEG', '.txt')
label_files.append(label_path)
f.close()
for label_file in label_files:
f = open(label_file)
for line in f:
temp = line.strip().split(" ")
if len(temp) > 1:
boxes.append(Box(0, 0, float(temp[3]), float(temp[4])))
if plus:
centroids = init_centroids(boxes, n_anchors)
else:
centroid_indices = np.random.choice(len(boxes), n_anchors)
centroids = []
for centroid_index in centroid_indices:
centroids.append(boxes[centroid_index])
# iterate k-means
centroids, groups, old_loss = do_kmeans(n_anchors, boxes, centroids)
iterations = 1
while (True):
centroids, groups, loss = do_kmeans(n_anchors, boxes, centroids)
iterations = iterations + 1
print("loss = %f" % loss)
if abs(old_loss - loss) < loss_convergence or iterations > iterations_num:
break
old_loss = loss
for centroid in centroids:
print(centroid.w * grid_size, centroid.h * grid_size)
# print result
for centroid in centroids:
print("k-means result:\n")
print(centroid.w * grid_size, centroid.h * grid_size)
label_path = "/raid/pengchong_data/Data/Lists/paul_train.txt"
n_anchors = 5
loss_convergence = 1e-6
grid_size = 13
iterations_num = 100
plus = 0
compute_centroids(label_path,n_anchors,loss_convergence,grid_size,iterations_num,plus)
3.2 YOLO的anchor机制和RPN的anchor有什么不同?
1.YOLO不是像RPN那样手选的先验框,而是通过k-means得到的。
2.YOLO的anchor 仅对长宽比进行了规定,并没有尺度的设置。
3.YOLO所得到的anchor框,是针对每个分割好的小区域进行的(需要做个转换),而RPN针对的是整个图片。
由于从标记文件的width,height计算出的anchor boxes的width和height都是相对于整张图片的比例,而YOLOv2通过anchor boxes直接预测bounding boxes的坐标时,坐标是相对于栅格边长的比例(0到1之间),因此要将anchor boxes的width和height也转换为相对于栅格边长的比例。转换公式如下:
w=anchor_widthinput_width/downsamples ;h=anchor_heightinput_height/downsamples
例如:
卷积神经网络的输入为416416时,YOLOv2网络的降采样倍率为32,假如k-means计算得到一个anchor box的anchor_width=0.2,anchor_height=0.6,则:
w=0.2416/32=0.213=2.6;h=0.6416/32=0.6*13=7.8
4、 锚框自学习: Guided Anchoring
paper: Region Proposal by Guided Anchoring
Anchor 的弊端之一是超参的人工设计与正负样本不均衡,并且无法很好地处理极端大小宽高物体,如果能自动地设计出更加优越高效的 Anchor,也是一种解决思路。基于此思想,商汤提出了锚框自学习 (Guided Anchoring) 算法,能够根据图像的特征自动地预测 Anchor 的位置和形状,生成一组稀疏但高效的 Anchor,全程无须人工的设计,并且还设计了 Feature Adaption 模块来修正特征图使之与 Anchor 形状更加匹配。




5、 谈谈 Anchor 设计准则
(1) Alignment: Alignment 是指 anchor 的中心点要和 feature 的位置对齐。由于每个 anchor 都是由 feature map 上的一个点表示,那么这个 anchor 最好是以这个点为中心,否则位置偏了的话,这个点的 feature 和这个 anchor 就不能非常好地对应起来,用该 feature 来预测 anchor 的分类和回归会有问题。我们设计了类似 cascade/iterative RPN 的实验来证明这一点,对 anchor 进行两次回归,第一次回归采用常规做法,即中心点和长宽都进行回归,这样第一次回归之后,anchor 中心点和 feature map 每一个像素的中心就不再完全对齐。我们发现这样的两次 regress 提升十分有限。所以我们在形状预测分支只对 w 和 h 做预测,而不回归中心点位置。
(2) Consistency: Consistency 是指 anchor 的特征要和形状匹配。这条准则是我们设计 feature adaption 的初衷,由于每个位置 anchor 形状不同而破坏了特征的一致性,我们需要通过 feature adaption 来进行修正。这条准则本质上是对于如何准确提取 anchor 特征的讨论。对于两阶段检测器的第二阶段,我们可以通过 RoI Pooling 或者 RoI Align 来精确地提取 RoI 的特征。但是对于 RPN 或者单阶段检测器的 anchor 来说,由于数量巨大,我们不可能通过这种 heavy 的方法来实现特征和框的精确 match,还是只能用特征图上一个点,也就是 512 × 1 × 1 512\times1\times1512×1×1 的向量来表示。那么 Feature Adaption 起到了一个让特征和 anchor 对应更加精确的作用,这种设计在其他地方也有可以借鉴之处。


























 326
326

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?










