MATLAB 分析FIR 滤波器的相位特性和幅度特性

一、实验目的
1. 了解 FIR 滤波器具有线性相位的条件。

2. 了解四种类型 FIR 滤波器的幅频特性和相频特性及用途。

3. 学会用 MATLAB 工具分析FIR 滤波器。二、 实验原理与方法
实验十六中已经讲过脉冲相应的对称与反对称，即满足h(n) = h(M − 1 − n) 为对称

满足h(n) = −h(M − 1 − n) 为反对称。当在 M  
为奇数和偶数下结合对称和反对称的情况，就可以得到四种类型的线性相位 FIR  滤波器。对其中每种类型其频率响应函数都有特有的表达式和独特的形状。可将 H (e ʲw ) 写成：

 

可得 Hr (0) = 0 ，不适合作低通。也是适合用来设计数字希尔伯特变换器和微分器的。

MATLAB 中用函数Hr_Type4 来计算振幅响应。
三、实验内容
1.复习课本中的有关内容，并阅读本实验原理。
2.设一个FIR 滤波器的单位脉冲响应为h=[1,2,3,2,1],编写一个MATLAB 函数验证它具有
线性相位。
可能用到的 MATLAB 函数有：freqz—求频率特性，real—求复数的实部，atan—求反正切。
3.  当 h=[1,2,3,-3-2,-1]时，重复实验内容 2，并比较两者的差异。
4.   当 FIR   滤波器的单位脉冲响应分别为 h=[1,-2,3,5,3,-2,1] ， h=[1,-2,3,3,-2,1] ，
h=[1,-2,3,5,-3,2,-1]  h=[1,-2,3,-3,2,-1]时 指出它们各属于何种类型的滤波器 并编写MATLAB
函数画出它们的幅频特性曲线和 H (z) 的零点位置。
参考流程图
1. 线性相位

2.幅频特性

四、 思考题
①什么 FIR 滤波器必须具有对称性？分别有哪几对称性？
②在四种类型的滤波器中，那种滤波器的应用最为广泛？为什么？
③Ⅱ型滤波器，Ⅲ型滤波器，Ⅳ型滤波器各不能用于何种滤波器？
五、实验报告要求
1.简述实验目的及原理。
2.整理好经过运行并证明是正确的实验程序并加上注释。绘出相应的图形。
3.简要回答思考题。

h=[1,2,3,2,1];
[H,p,w]=dtft(h);
subplot(221),plot(w/pi,p);grid;
axis([0,1,-4,4]);
title('相频特性');
subplot(222),grpdelay(h,1);
h=[1,2,3,-3,-2,-1];
[H,p,w]=dtft(h);
subplot(223),plot(w/pi,p);grid;
axis([0,1,-4,4]);
title('相频特性');
subplot(224),grpdelay(h,1);
调用的函数：dtft.m
function[m,a,w]=dtft(x)
N=length(x);
n=0:N-1;
w=linspace(-2*pi,2*pi,500);
y=x*exp(-j*n'*w);
m=abs(y);
a=angle(y);

h1=[1,-2,3,5,3,-2,1];
h2=[1,-2,3,3,-2,1];
h3=[1,-2,3,5,-3,2,-1];
h4=[1,-2,3,-3,2,-1];
figure;
[a1,w1,type1,tao1]=amp(h1);type1
subplot(221),plot(w1/pi,abs(a1));
xlabel('*pi');
title('h1 幅频特性');
[a2,w2,type2,tao2]=amp(h2);type2
subplot(222),plot(w2/pi,abs(a2));
title('h2 幅频特性');
xlabel('*pi');
[a3,w3,type3,tao3]=amp(h3);type3
subplot(223),plot(w3/pi,abs(a3));
title('h3 幅频特性');
xlabel('*pi');
[a4,w4,type4,tao4]=amp(h4);type4
subplot(224),plot(w4/pi,abs(a4));
title('h4 幅频特性');
xlabel('*pi');
figure;
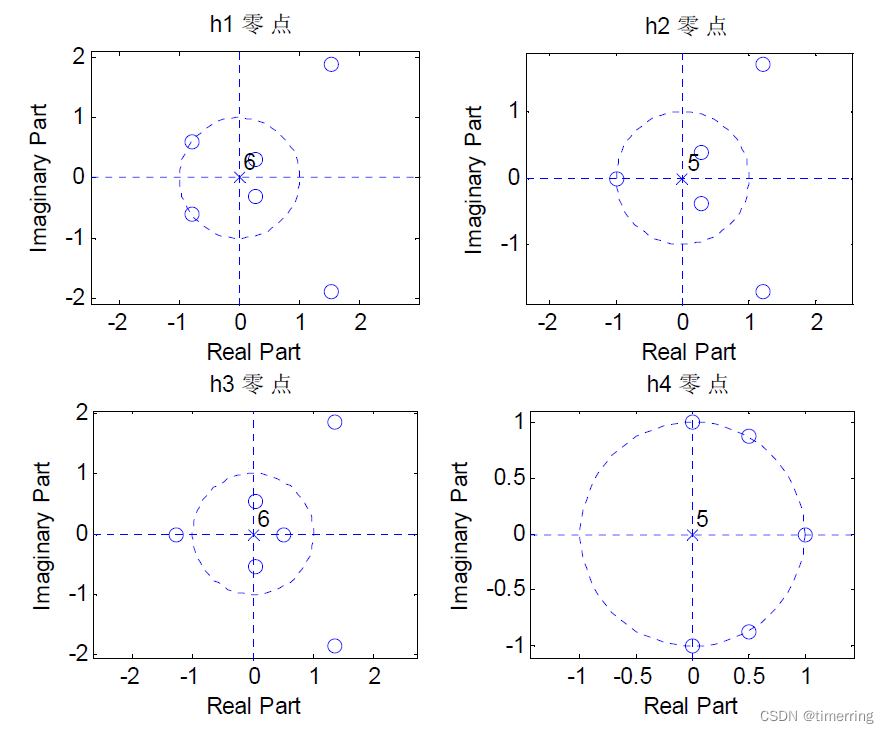
subplot(221),zplane(h1,1);title('h1 零点');
subplot(222),zplane(h2,1);title('h2 零点');
subplot(223),zplane(h3,1);title('h3 零点');
subplot(224),zplane(h4,1);title('h4 零点');
调用的函数：amp.m
function [A,w,type,tao]=amp(h);
N=length(h);
tao=(N-1)/2;
L=floor((N-1)/2);
n=1:L+1;
w=[0:500]*2*pi/500;
if all(abs(h(n)-h(N-n+1))<1e-10)
A=2*h(n)*cos(((N+1)/2-n)'*w)-mod(N,2)*h(L+1);
type=2-mod(N,2);
elseif all(abs(h(n)+h(N-n+1))<1e-10)&(h(L+1)*mod(N,2)==0)
A=2*h(n)*sin(((N+1)/2-n)'*w);
type=4-mod(N,2);
else disp('错误：这是非线性相位系统！');
[A,m,w]=dtft(h);
A=A.*exp(i*m);
type='?';
tao='?';
end