贝叶斯分类器详解

不会&编程

已于 2024-05-21 01:39:14 修改

阅读量962

点赞数 23

分类专栏： Python机器学习文章标签：概率论

于 2024-05-12 16:17:45 首次发布

本文链接：https://blog.csdn.net/m0_56878426/article/details/138472828

版权

Python机器学习专栏收录该内容

7 篇文章 0 订阅

订阅专栏

1 概率论知识

1.1 先验概率

先验概率是基于背景常识或者历史数据的统计得出的预判概率，一般只包含一个变量，例如P(A)，P(B)。

1.2 联合概率

联合概率指的是事件同时发生的概率，例如现在A,B两个事件同时发生的概率，记为P(A,B)、P(A∩B)、P(AB)。

若事件A和事件B相互独立，则有：

$P(A,B)=P(A)P(B)$

例子：假设事件A为明天上班，事件B为明天中彩票，其中P(A)=0.5，P(B)=0.5，则明天既上班又中彩票的概率为P(A)P(B)=0.25

1.3 条件概率

其中一般条件概率中的A事件表示结果，B事件表示原因，即由因求果

其中，P (AB) 就是联合概率。在A与B相互独立的情况下，易得:

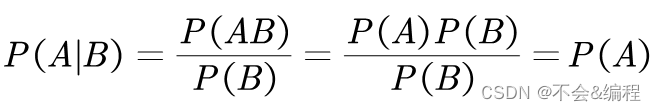
即B事件对A事件没有影响

1.4 后验概率

后验概率和条件概率的区别是：后验概率是由果求因：，例如，事件A是由事件B引起的，则P(A|B)是条件概率，P(B|A)是后验概率

举个通俗易懂的例子：

条件概率：新闻说今天路上出现了交通事故，若想推算一下因此而堵车的概率，也就是 P(堵车|交通事故)，这是由因推果。
后验概率：出门后路上遇到了堵车，若想推算一下这次堵车是由发生了交通事故而引起的概率，也就是后验概率 P(交通事故|堵车)，这是由果求因。

1.5 全概率公式

（1）样本空间

（2）全概率公式

1.6 贝叶斯公式

设样本空间为Ω，B为Ω中的事件， $A_{1},A_{2},\cdots ,A_{n}$ 为Ω的一个划分，且 $P(B) > 0, P(A_{i})>0,i = 1,2,\cdots,n$ ，则有：

$P(A_{i}|B)=\frac{P(B|A_{i})P(A_{i})}{\sum_{j=1}^{n} P(B|A_{j})P(A_{j})}, i=1,2,\cdots,n$

称上式为贝叶斯公式，也称为逆概率公式

2 贝叶斯分类器理论知识

2.1 朴素贝叶斯发的学习与分类

2.1.1 基本方法

设

输入空间： $\chi$ $\subseteq$ $\mathbb{R}^{n}$ 为n维集合的向量
输出空间：类标记集合 $\Upsilon =$ $\begin{Bmatrix} c_{1},c_{2},\cdots,c_{k} \end{Bmatrix}$
输入为特征向量： $x \in$ $\chi$
输出为类标记（class label）： $y \in$ $\Upsilon$

X是定义在输入空间 $\chi$ 上的随机向量，Y是定义在输出空间 $\Upsilon$ 上的随机变量。 $P(X,Y)$ 是X和Y的联合概率分布。训练数据集

$T=\begin{Bmatrix} \begin{pmatrix} x_{1},y_{1} \end{pmatrix}, \begin{pmatrix} x_{2},y_{2} \end{pmatrix},\cdots,\begin{pmatrix} x_{N},y_{N} \end{pmatrix} \end{Bmatrix}$

是 $P(X,Y)$ 独立同分布产生

朴素贝叶斯法通过训练数据集学习联合概率分布 $P(X,Y)$ ,学习过程如下：

（1）学习先验概率分布及条件概率分布

先验概率分布： $P(Y=c_{k}),k=1,2,\cdots,K$
条件概率分布： $\mbox{$P(X=x|Y=c_{k})=P(X^{(1)}=x^{(1)},\cdots,X^{(n)}=x^{(n)}|Y=c_{k}), k=1,2,\cdots,K$}$

假设 $x^{(j)}$ 可取值有 $S_{j}$ 个， $j=1,2,\cdots,n$ ,Y的可能取值有K个，那么参数的个数有 $K\prod_{j=1}^{n}S_{j}$ ，因此条件概率分布 $P(X=x|Y=c_{k})$ 有指数级别数量的参数，其估计实际是不可行的

朴素贝叶斯法对条件概率分布作了条件独立性的假设。由于这是一个较强的假设，朴素贝叶斯法也由此得名。朴素贝叶斯法的条件独立性假设为：

$\mbox{$P(X=x|Y=c_{k})=P(X^{(1)}=x^{(1)},\cdots,X^{(n)}=x^{(n)}|Y=c_{k})=\prod_{j=1}^{n}P(X^{(j)}=x^{(j)}|Y=c_{k}) ~~~(1)$}$

朴素贝叶斯法实际上学习到生成数据的机制，所以属于生成模型。条件独立假设等于是说用于分类的特征在类确定的条件下都是条件独立的。这一假设使朴素贝叶斯法变得简单，但有时会牺牲一定的分类准确率。

朴素贝叶斯分类时，对给定的输入x，通过学习到的模型计算后验概率分布 $P(X=x|Y=c_{k})$ ，将后验概率最大的类作为x的类输出，后验概率计算根据贝叶斯定理进行：

$\mbox{$P(Y=c_{k}|X=x) = \frac{P(X=x|Y=c_{k})P(Y=c_{k})}{\sum_{k}P(X=x|Y=c_{k})P(Y=c_{k})}~~~(2)$}$

将公式（1）代入到公式（2）可得：

$\mbox{$P(Y=c_{k}|X=x) = \frac{P(Y=c_{k})\prod_{j}P(X^{(j)}=x^{(j)}|Y=c_{k})}{\sum_{k}P(Y=c_{k})\prod_{j}P(X^{(j)}=x^{(j)}|Y=c_{k})}~k=1,2,\cdots,K~~~(3)$}$

于是，朴素贝叶斯分类器可表示为：

$\mbox{$y=f(x)=argmax_{c_{k}}P(Y=c_{k}|X=x) = \frac{P(Y=c_{k})\prod_{j}P(X^{(j)}=x^{(j)}|Y=c_{k})}{\sum_{k}P(Y=c_{k})\prod_{j}P(X^{(j)}=x^{(j)}|Y=c_{k})}~~~(4)$}$

由于分母是一样的，所以可以简化为：

$\mbox{$y=f(x)=argmax_{c_{k}}P(Y=c_{k})\prod_{j}P(X^{(j)}=x^{(j)}|Y=c_{k})~~~(5)$}$

2.1.2 后验概率最大化含义

朴素贝叶斯会将实例分到后验概率最大的类中，即等价于期望风险最小化，假设选择0-1损失函数：

$L(Y,f(X))=\left\{\begin{matrix} 1,Y \neq f(X)& \\ 0,Y=f(X)& \end{matrix}\right.$

其中 $f(X)$ 是分类决策函数。这时，期望风险函数为

$R_{exp}(f)=E[L(Y,f(X))]$

期望是对联合分布 $P(X,Y)$ 取的。所以取条件期望

$R_{exp}(f)=E_{X}\sum_{k=1}^{K}[L(c_{k},f(X))]P(c_{k}|X)$

为了使期望风险最小化，只需对 $X=x$ 逐个最小化，因此有

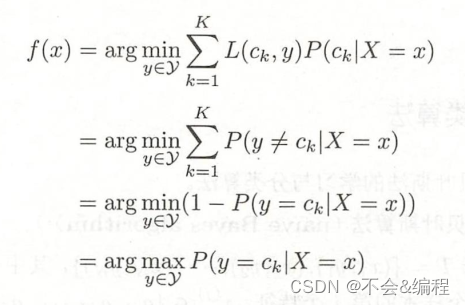
最终可知后验概率最大的类=期望风险最小的类，即朴素贝叶斯采用的原理：

$f(x)=argmax_{c_{k}}P(c_{k}|X=x)$

2.2 朴素贝叶斯法的参数估计

2.2.1 极大似然估计

2.2.2 学习与分类算法

1 算法流程

2 例子

2.2.3 贝叶斯估计

1 理论

2 例子

取λ=1，之后如下所示：

不会&编程

关注

23
点赞
踩
9

收藏

觉得还不错? 一键收藏
1
评论
贝叶斯分类器详解

例子：假设事件A为明天上班，事件B为明天中彩票，其中P(A)=0.5，P(B)=0.5，则明天既上班又中彩票的概率为P(A)P(B)=0.25。联合概率指的是事件同时发生的概率，例如现在A,B两个事件同时发生的概率，记为P(A,B)、P(A∩B)、P(AB)。先验概率是基于背景常识或者历史数据的统计得出的预判概率，一般只包含一个变量，例如P(A)，P(B)。：，例如，事件A是由事件B引起的，则P(A|B)是条件概率，P(B|A)是后验概率。其中一般条件概率中的A事件表示结果，B事件表示原因，即。
复制链接

扫一扫