谷歌TPU_脉动阵列实现矩阵乘法（附完整Verilog代码）

力争上游_

已于 2025-02-27 09:56:25 修改

阅读量1.3w

点赞数 47

文章标签： fpga开发矩阵神经网络硬件架构

于 2023-12-13 00:20:51 首次发布

本文链接：https://blog.csdn.net/m0_57102661/article/details/134960925

版权

谷歌TPU_脉动阵列实现矩阵乘法（附完整Verilog代码）

一、谷歌TPU介绍
- TPU计算核心的硬件架构
二、矩阵乘法单元硬件架构
三、脉动阵列实现矩阵乘法原理
四、Verilog实现

一、谷歌TPU介绍

谷歌的 TPU（张量处理单元）是一种专门为机器学习工作负载优化的定制硬件加速器。TPU 通过高效地执行矩阵乘法、卷积运算和其他常见的神经网络操作，以提供比传统 CPU 或 GPU 更快的训练和推理性能。
谷歌 TPU 的基本构建块是一个称为 TPU 芯片的 ASIC（应用特定集成电路），其中包含了数千个小型处理单元，它们被称为“计算核心”或“TPU 内核”。这些内核提供了高度并行的计算能力，并且专门优化了常见的矩阵操作，如卷积和矩阵乘法。每个 TPU 芯片还包含了多个存储器子系统，包括高速缓存、本地共享内存和全局存储器。数据可以在这些存储器之间传输，以支持不同类型的计算和数据流。为了实现更高的性能和可扩展性，多个 TPU 芯片可以组合成一个称为 TPU Pod 的集群。TPU Pod 中的每个 TPU 芯片都能够直接访问其他芯片的存储器，因此可以实现高效的数据通信和更大规模的计算。除了硬件之外，谷歌还提供了一系列的软件工具来支持 TPU 的使用。例如，TensorFlow 框架可以通过编写特定的代码来利用 TPU 的计算能力，并且谷歌还提供了一些高级优化工具，如 XLA 编译器，以进一步提高性能和效率。总的来说，谷歌 TPU 的硬件架构部分采用了定制化的设计，以支持高度并行的计算和专门优化的矩阵操作。TPU Pod 集群也提供了更高的可扩展性和性能，使得它们适合于大规模的深度学习任务。TPU 最初是为了支持谷歌的机器学习框架 TensorFlow 而开发的，但它也可以与其他机器学习框架一起使用。Google Cloud 平台上的用户可以通过 Cloud TPU 服务来访问这些加速器，以加快他们的机器学习工作负载。
总的来说，TPU 是一种设计用于加速机器学习工作负载的定制硬件加速器，对于大规模的深度学习任务提供了高性能和能效。

TPU计算核心的硬件架构

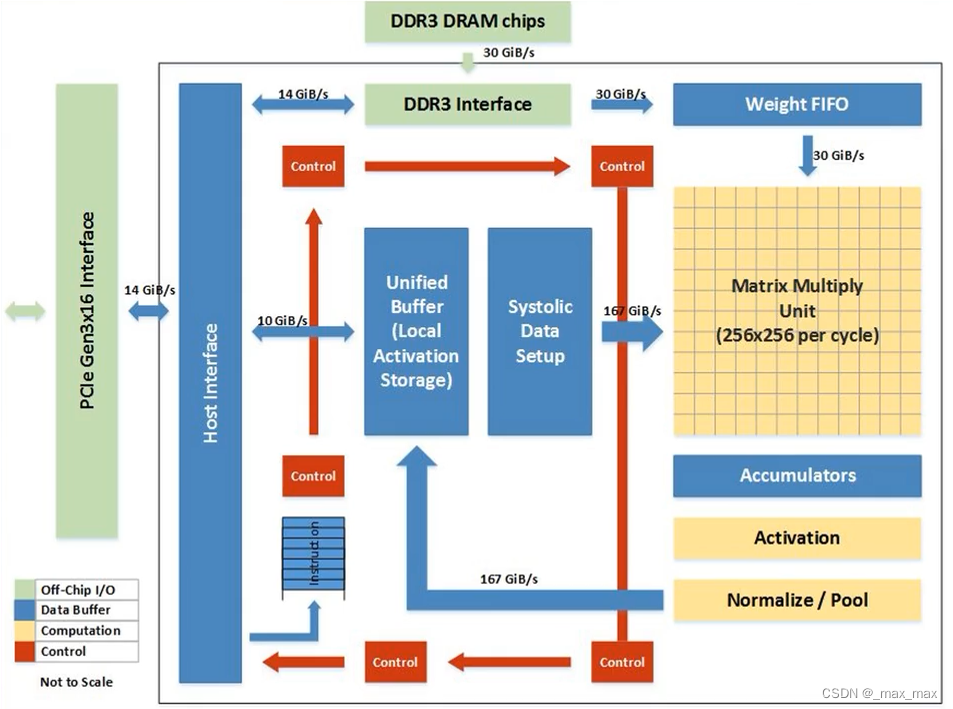
下图为TPU计算核心的硬件架构，主要包含以下几部分：

矩阵乘法单元（Matrix Multiply Unit）：矩阵乘法是深度学习中常见的计算操作之一，TPU 的计算核心专门针对矩阵乘法进行了优化。它包含多个乘法和累加器单元，以高效地执行大规模矩阵乘法运算。
卷积单元（Convolution Unit）：卷积操作是卷积神经网络（CNN）中常用的操作，TPU 的计算核心也针对卷积操作进行了优化。卷积单元具有特定的硬件结构，可以高效地执行卷积计算。
存储器子系统（Memory Subsystem）：TPU 的计算核心包含多个存储器子系统，用于存储权重、输入数据和中间结果。这些存储器子系统包括高速缓存、本地共享内存和全局存储器，可以在不同的存储器之间进行数据传输，并且能够支持快速的访问和数据流。
控制逻辑（Control Logic）：TPU 的计算核心还包括控制逻辑单元，用于指导和管理计算操作的执行。控制逻辑负责调度和协调不同的计算单元，并确保计算操作按照正确的顺序和时序进行。
这些部分共同组成了一个 TPU 计算核心的架构。通过高度并行的设计和针对矩阵乘法、卷积等常见操作的优化，TPU 的计算核心可以提供高性能和能效，适用于大规模的深度学习任务。
本文将介绍TPU中的矩阵乘法单元（Matrix Multiply Unit），并编写Verilog代码实现其功能，并仿真验证其功能，之后的文章会完成卷积单元（Convolution Unit）的部分，并进行开源。

二、矩阵乘法单元硬件架构

TPU 中的矩阵乘法单元（Matrix Multiply Unit）是其硬件架构中的关键部分，它专门针对大规模矩阵乘法操作进行了优化。下面是矩阵乘法单元的硬件架构主要特点：

数学计算单元：矩阵乘法单元包含大量的数学计算单元，用于执行乘法和累加操作。这些计算单元能够并行地处理多个元素，从而实现高效的矩阵乘法计算。
数据流水线：矩阵乘法单元通常采用数据流水线的设计，将矩阵乘法操作划分为多个阶段，并在不同阶段并行地处理不同的数据。这样可以充分利用硬件资源，提高计算效率。
数据存储和交换：矩阵乘法单元需要大量的数据存储和交换能力，以便及时获取输入数据、存储中间结果，并输出最终的计算结果。因此，在硬件架构中通常包括了高速缓存、寄存器文件等数据存储单元，以及专门的数据总线和交换逻辑。
控制逻辑和调度器：矩阵乘法单元中还包含了控制逻辑和调度器，用于管理和协调不同计算单元之间的工作。控制逻辑负责指导数据流的处理顺序，保证计算操作的正确执行。
总的来说，矩阵乘法单元在硬件架构中具有高度并行的设计，以支持大规模矩阵乘法运算。它通过优化的数据流水线、数据存储和交换机制，以及有效的控制逻辑，实现了对矩阵乘法操作的高效执行。
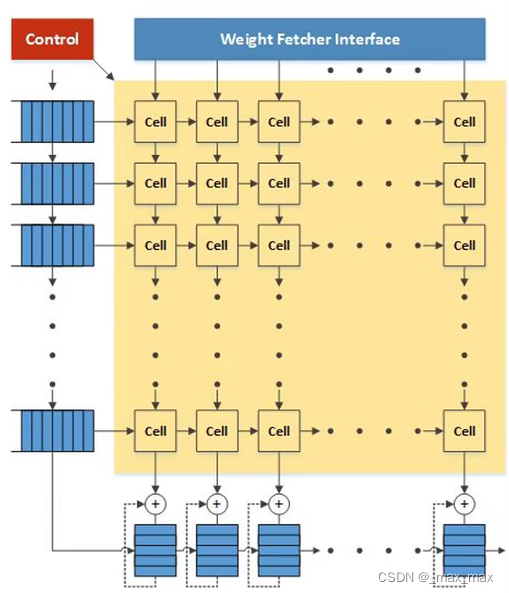
下图是TPU中乘法单元的硬件架构图，核心部分是多个Cell组成的计算阵列，阵列的左侧和上侧分别是处理后的两个矩阵的行和列数据，矩阵数据跟随时钟上升沿在阵列中有规律的流动，因此得名脉动阵列，使用脉动阵列实现矩阵乘还可以减少数据存取的次数，进而消除存储墙，实现高性能的存内计算。

三、脉动阵列实现矩阵乘法原理

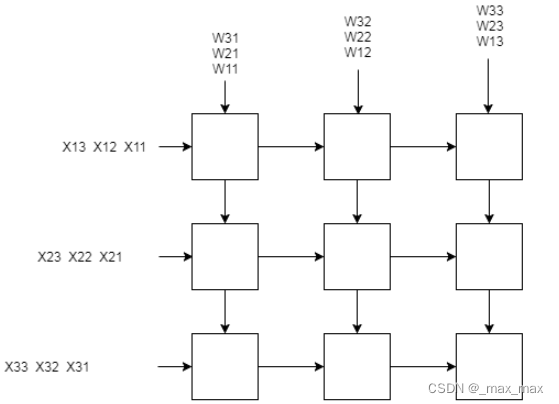
在这里插入图片描述
如上图所示，以一个3乘3和3乘3的矩阵相乘为例，第一个矩阵的数据为[[X11,X12,X13],[X21,X22,X23],[X31,X32,X33]]，第二个矩阵的数据为[[W11,W12,W13],[W21,W22,W23],[W31,W32,W33]]数据按上图顺序依次输入阵列，阵列单元PE完成乘加操作，并把来自左边的数据往右传，把来自上边的数据往下传，各PE单元中除了乘加单元，也有存放sum的寄存器，把和进行保存。对于n乘n和n乘n的矩阵，共需要n^2-2个周期，就能完成计算。
脉动阵列的特点：
• 每个PE只与其邻近的PE进行通信，PE之间的通信具有局部性，而且通信是规则的。
• 每一个PE都是相同的,但个别也可以不同（边缘的PE不同）。
• 通过时钟激励统一处理。

四、Verilog实现

PE单元

PE单元实现乘加操作，并配有寄存器能存储和(sum)数据，Verilog代码如下：

module pe(clk,rst,left,up,down,right,sum_out);
input clk;
input rst;
input [3:0] left;
input [3:0] up;
output reg [3:0] down;
output reg [3:0] right;
output reg [7:0] sum_out;
wire [7:0] mult_out;
always@(posedge clk)begin
    if(rst) begin
        right<=0;
        down<=0;
        sum_out<=0;
        end
    else begin
        down<=up;
        right<=left;
        sum_out<=sum_out+mult_out;
    end
end
multiply u_mult(
    .a(left),
    .b(up),
    .out(mult_out)
);

endmodule

PE中例化的乘法器，可自行设置，可根据需要设置为半精度、单精度、双精度等，在这里使用普通的十进制乘法器，代码如下：

module multiply(a,b,out);
input [3:0]a;
input [3:0]b;
output wire [7:0] out;
assign out=a*b;
endmodule

顶层文件

脉动阵列顶层模块中例化了9个PE单元，顶层模块代码如下：

module top(clk,rst,en,in1,in2,out);
input clk;
input rst;
input en;
input [4*9-1:0] in1;
input [4*9-1:0] in2;
output reg [9*9-1:0] out;
reg [3:0] hang1 [0:4];
reg [3:0] hang2 [0:4];
reg [3:0] hang3 [0:4];
reg [3:0] lie1 [0:4];
reg [3:0] lie2 [0:4];
reg [3:0] lie3 [0:4];
reg [3:0] flag;
wire [3:0] down00,down01,down02,down10,down11,down12,down20,down21,down22;
wire [3:0] right00,right01,right02,right10,right11,right12,right20,right21,right22;
wire [7:0] sum00,sum01,sum02,sum10,sum11,sum12,sum20,sum21,sum22;
reg [3:0] left00;
reg [3:0] left10;
reg [3:0] left20;
reg [3:0] up00;
reg [3:0] up01;
reg [3:0] up02;
always@(posedge clk)begin
    if(rst)begin
        out<=0;
    end
    else begin
        hang1[0]<=in1[3-:4];
        hang1[1]<=in1[7-:4];
        hang1[2]<=in1[11-:4];
        hang1[3]<=4'b0000;
        hang1[4]<=4'b0000;
        hang2[0]<=4'b0000;
        hang2[1]<=in1[15-:4];
        hang2[2]<=in1[19-:4];
        hang2[3]<=in1[23-:4];
        hang2[4]<=4'b0000;
        hang3[0]<=4'b0000;
        hang3[1]<=4'b0000;
        hang3[2]<=in1[27-:4];
        hang3[3]<=in1[31-:4];
        hang3[4]<=in1[35-:4];
        lie1[0]<=in2[3-:4];
        lie1[1]<=in2[15-:4];
        lie1[2]<=in2[27-:4];
        lie1[3]<=4'b0000;
        lie1[4]<=4'b0000;
        lie2[0]<=4'b0000;
        lie2[1]<=in2[7-:4];
        lie2[2]<=in2[19-:4];
        lie2[3]<=in2[31-:4];
        lie2[4]<=4'b0000;
        lie3[0]<=4'b0000;
        lie3[1]<=4'b0000;
        lie3[2]<=in2[11-:4];
        lie3[3]<=in2[23-:4];
        lie3[4]<=in2[35-:4];
    end
end
always@(posedge clk)
    if(rst)begin
        flag<=0;
        end
    else if(en) begin
        //if(flag==4'd5)
            //flag<=0;
            //else
            flag<=flag+1;
    end
always@(posedge clk)begin
    case(flag)
        0 : begin
            left00<=hang1[0];
            left10<=hang2[0];
            left20<=hang3[0];
            up00<=lie1[0];
            up01<=lie2[0];
            up02<=lie3[0];
            end
        1 : begin
            left00<=hang1[1];
            left10<=hang2[1];
            left20<=hang3[1];
            up00<=lie1[1];
            up01<=lie2[1];
            up02<=lie3[1];
            end
        2 : begin
            left00<=hang1[2];
            left10<=hang2[2];
            left20<=hang3[2];
            up00<=lie1[2];
            up01<=lie2[2];
            up02<=lie3[2];
            end
        3 : begin
            left00<=hang1[3];
            left10<=hang2[3];
            left20<=hang3[3];
            up00<=lie1[3];
            up01<=lie2[3];
            up02<=lie3[3];
            end
        4 : begin
            left00<=hang1[4];
            left10<=hang2[4];
            left20<=hang3[4];
            up00<=lie1[4];
            up01<=lie2[4];
            up02<=lie3[4];
            end
        default : begin
            left00<=0;
            left10<=0;
            left20<=0;
            up00<=0;
            up01<=0;
            up02<=0;
            end
    endcase
    
    end
    
pe pe00(
    .clk(clk),.rst(rst),.left(left00),.up(up00),.down(down00),.right(right00),.sum_out(sum00)
);
pe pe01(
    .clk(clk),.rst(rst),.left(right00),.up(up01),.down(down01),.right(right01),.sum_out(sum01)
);
pe pe02(
    .clk(clk),.rst(rst),.left(right01),.up(up02),.down(down02),.right(right02),.sum_out(sum02)
);
pe pe10(
    .clk(clk),.rst(rst),.left(left10),.up(down00),.down(down10),.right(right10),.sum_out(sum10)
);
pe pe11(
    .clk(clk),.rst(rst),.left(right10),.up(down01),.down(down11),.right(right11),.sum_out(sum11)
);
pe pe12(
    .clk(clk),.rst(rst),.left(right11),.up(down02),.down(down12),.right(right12),.sum_out(sum12)
);
pe pe20(
    .clk(clk),.rst(rst),.left(left20),.up(down10),.down(down20),.right(right20),.sum_out(sum20)
);
pe pe21(
    .clk(clk),.rst(rst),.left(right20),.up(down11),.down(down21),.right(right21),.sum_out(sum21)
);
pe pe22(
    .clk(clk),.rst(rst),.left(right21),.up(down12),.down(down22),.right(right22),.sum_out(sum22)
);

endmodule

Testbench文件

顶层模块的仿真测试文件如下：

`timescale 1ns / 1ps
module top_tb();
reg clk;
reg rst;
reg en;
reg [4*9-1:0] in1;
reg [4*9-1:0] in2;
wire [9*9-1:0] out;
initial begin
    clk=0;
    rst=0;
    in1=0;
    in2=0;
    en=0;
    #10
    rst=1;
    #10
    rst=0;
    in1=36'b0101_0010_0011_0011_0101_0010_0010_0100_0011;
    in2=36'b0101_0010_0011_0011_0101_0010_0010_0100_0011;
    #10
    en=1;
    #100
    $finish;
    
    end
always
    #5
    clk=~clk;
top u_top(
    .clk(clk),
    .rst(rst),
    .in1(in1),
    .in2(in2),
    .out(out),
    .en(en)
    );

endmodule

仿真结果

仿真测试的功能是进行
[[3,4,2],
[2,5,3],
[3,2,5]]矩阵和
[[3,4,2],
[2,5,3],
[3,2,5]]相乘，
最后的结果是
[[23,36,28],
[25,39,34],
[28,32,37]]
脉动阵列的数据流输入如下图所示：
在这里插入图片描述
仿真结果波形图如下图所示：

仿真结果数据正确，且各PE最终结果产生的时序正确。
整体工程已上传个人github仓库，之后会完成谷歌TPU中的脉动阵列实现卷积操作的项目并开源。