目录
概述
网上看了很多关于FFT的解释,但他们大都是用于算法加速(快速计算多项式乘法),而本文将从另一个角度来说明FFT的其他作用-----信号处理领域的天才工具
首先是名词解释
| 缩写 | 英文 | 中文 |
|---|---|---|
| FT | Fourier Transform | 傅里叶变换 |
| DFT | Discrete Fourier Transform | 离散傅里叶变换 |
| FFT | Fast Fourier Transform | 快速傅里叶变换 |
| IFT | Inverse Fourier Transform | 傅里叶逆变换 |
| IDFT | Inverse Discrete Fourier Transform | 离散傅里叶逆变换 |
| IFFT | Inverse Fast Fourier Transform | 快速傅里叶逆变换 |
之后是他们的关系
FT是最基础的一种变换,IFT则是FT的逆运算
DFT是离散化的FT(计算机只能处理离散数据)
FFT则是DFT的一种快速运算方法
IDFT和IFFT则分别是DFT和FFT的逆运算
数学基础
微积分
微积分基础(高数)还是得有的,请自行收看B站视频
复数
定义

就是一个复数
共轭复数:

加减法:
乘法:
复平面
我们以实轴为横轴,虚轴为纵轴,建立平面直角坐标系,这个坐标系所在的平面被称为复平面
复数形式
对应着复平面中唯一确定的一点

欧拉公式
通过公式可以看出,
是复平面上的一个单位圆
随着x的增加,代表红色的点沿着逆时针方向进行旋转

关于复数和复平面的详情请看 复变函数
单位根及性质
定义
的根
在复数范围内的,n次单位根有n个
它们将复平面单位圆等分为n份
记作
根据定义
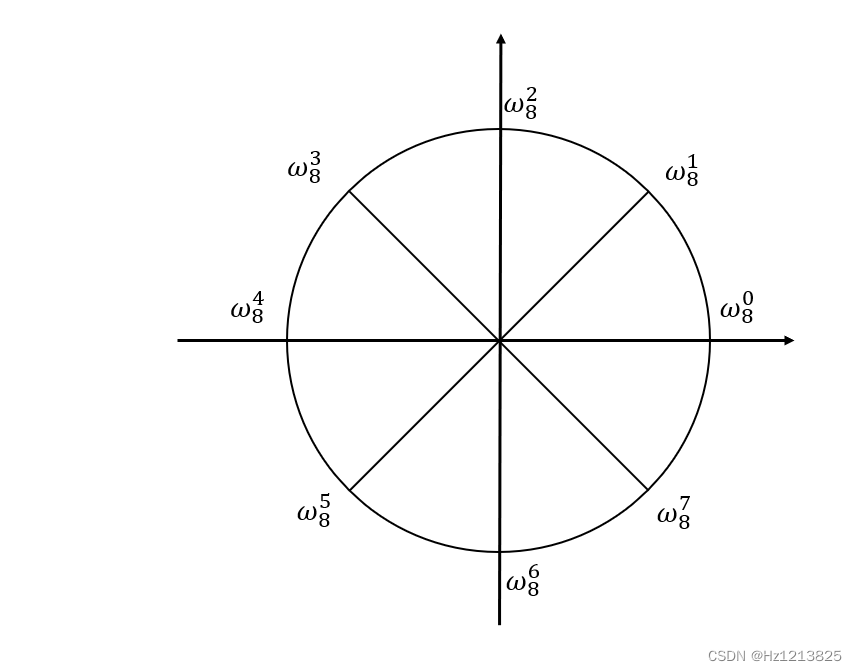
单位根性质1:
证明:
单位根性质2:
根据欧拉公式可以知道
证明:
单位根性质3:
带进去就行,证明略
单位根性质4:
证明:
单位根性质5:
带进去就行,证明略
另外
根据欧拉公式可以知道
证明:
傅里叶变换(FT)
咱不是数学家,不谈原理,只谈应用
傅里叶变换(FT)就是一种人为发明的数学工具
作用
作用就一句话:将时域信号转为频域
这也是电学老师最常挂在嘴边的一句话
通俗理解:
我们来设想这样一个场景,现在要求这个函数
的图像
那很简单,只需要将每个点带入函数求出值,并将其画出即可,就像下图
如果这个信号是现实中的某个信号(如声音)
横轴是以时间,纵轴是现实中的物理量(如电压),则这个图像是信号在时域中的表现

而如果我们知道这个图像想要求出上式中的各项的
及其系数呢?
这就是傅里叶变换所解决的事情
如下图,横轴是 f(t) 的每个asin(wt)的w,FT有对称性,忽略负半轴
纵轴与函数的a相关,则这个图像是信号在频域中的表现

所以,傅里叶变换就是一种将组合起来的信号拆解开来的工具
这是非常反直觉的,但经过数学上的严格证明
它为我们提供了 一种新的信号分析的手段
公式
傅里叶变换公式:
计算时只需要把复数分为实部和虚部分别积分即可
频域的相关解释
可能原意动手的小伙伴已经发现了,好像并不能直接计算出 sin(t) 的傅里叶变换
得出上式是根据傅里叶函数的定义和一个另外的构造函数(单脉冲函数)来的
具体的手算FT的过程请看积分变换
每一个函数均可以写成有限或无限个正弦函数的和,即
下图中的横坐标自然是原函数 f(t)中每一个
的
这个图仅仅表现频率的性质,而还有相位信息没有表现出来,因此表现出
关于0对称的图像
纵坐标是傅里叶变换的结果的模(傅里叶变换的结果是复变函数),这里常用模值
而与幅值的对应关系是互为 相反数的两个赋值的和/2
即w=1的幅值
注意:本图也是网上最常见到的图(幅度谱),只表现出了频率(w),并没有表现出相位

这个图则是刚才函数的相位谱

以
的两个点为例子来解释下
这两个点在幅度谱和相位谱的值分别代表这项展开式
中的
和
所以这项可以表示为
傅里叶逆变换(IFT)
能将时域转化为频域进行处理,这是信号处理的一大进步,
但往往我们需要将这个频域信号转化会时域信号才能让其发挥作用
如音频处理中,如果要消除某个高频(低频)的噪声,我们要得到的肯定是时域信号,频域的信号不能被人耳所识别
这就需要本节提到的傅里叶逆变换了
公式
和傅里叶变换的公式相比,是改变了系数,被积分的量由时域信号换为了频域信号,附带的算子
换成了
在计算上(尤其是计算机的计算)没有特别大的区别,仅仅是更改了输入输出和某一个(sin项(欧拉公式展开后))的符号而已
离散傅里叶变换(DFT)
因为计算机只能处理离散化的数据(采样不可能做到实时),因此在处理傅里叶变换时需要将其进行离散化,也就是离散傅里叶变换(DFT)
公式
X(m)就是DFT之后的频域信号,因为是离散的,因此频域信号是一个个孤立的点
x(n)是采集到的时域的信号,需要每隔固定的时间进行采集
N是采集的信号和输出信号的数量
欧拉公式
代表着在复平面上一个点随着x的增加沿着单位圆而逆时针旋转
因为在连续傅里叶变换中是
的积分,因此
中的t代表将复平面的单位圆分为无数个小份进行求和(积分)
而在DFT中,则需要对整个单位圆间隔一段距离进行采样计算,也就是
中的

DFT的实现
因为使用到了复数运算,因此我们先建立一个复数结构体
typedef struct __complex
{
float real;
float imaginary;
}complex;之后是复数的基本运算
complex complex_multiplication(complex a, complex b)
{
complex zj;
zj.real = a.real*b.real - a.imaginary*b.imaginary;
zj.imaginary = a.real*b.imaginary + a.imaginary*b.real;
return zj;
}
complex complex_add(complex a, complex b)
{
complex zj;
zj.real = a.real + b.real;
zj.imaginary = a.imaginary + b.imaginary;
return zj;
}
complex complex_subtraction(complex a, complex b)
{
complex zj;
zj.real = a.real - b.real;
zj.imaginary = a.imaginary - b.imaginary;
return zj;
}根据DFT的公式可以看出
每计算一个m的值,需要经历从0到N-1的一个累加
而x(n)是复数,
可以使用欧拉公式展开为复数
所以只需要进行一个复数的乘法即可
#define PI (3.1415926)
void DFT(complex *Input, complex *Output,int Len)
{
complex zj,zj1;
for (int k = 0; k < Len; k++)
{
zj.real = 0;
zj.imaginary = 0;
for (int n = 0; n < Len; n++)
{
zj1.real= cos(2 * PI*k*n / Len);
zj1.imaginary= -sin(2 * PI*k*n / Len);
zj1=complex_multiplication(zj1, Input[n]);
zj = complex_add(zj, zj1);
}
Output[k] = zj;
}
}首先输入的是复数数组x(k),输出数组X(k),还有长度N
之后是扫描k 从0到N-1,这步是计算频域中每一个离散点
再之后就是扫描n 也是从0到N-1,是一个累加,再确定k的条件下计算
具体是设置中间变量 zj , zj1,他们都是复数,zj用于存储每个不同k的累加数据
而zj1则用于存储不同k时的算子
之后进行复数乘法和累加到zj中后放入输出的指定位置即可
离散傅里叶逆变换(IDFT)实现
IDFT的公式是
从公式可以看出, 我们只需要将DFT的算法进行一点改变即可变为IDFT
首先是在进行复数乘法之前,将-sin项变为sin即可,也就是乘-1
之后是在输出时虚部和实部均 / N(这里是Len)
其余地方无需改动
void DFT(complex *Input, complex *Output,int Len,int inverse)
{
complex zj,zj1;
for (int k = 0; k < Len; k++)
{
zj.real = 0;
zj.imaginary = 0;
for (int n = 0; n < Len; n++)
{
zj1.real= cos(2 * PI*k*n / Len);
zj1.imaginary = inverse *-sin(2 * PI*k*n / Len);
zj1=complex_multiplication(zj1, Input[n]);
zj = complex_add(zj, zj1);
}
if (inverse == -1)
{
zj.real /= Len;
zj.imaginary /= Len;
}
Output[k] = zj;
}
}DFT的结果含义
首先说明一点,DFT是关于
对称的
根据采样定理,想要不失真获得原始信号,则采样频率需要至少为原频率的2倍,我们一般取左半为有效信号
某个信号的幅值谱如下 ,我们要根据这个计算信号的频率幅值和相位(展开成
)的
另外因为截取的信号不是完整周期的信号,因此会出现频谱泄露
所以求相位的方法是先找到频率,在找到频率对应的那个x(k)的虚部和实部求得相位

设采样信号的频率为
,采样点的数量为N
则
的对应的频率为
,分辨率为
幅值在除了直流分量(
)处为
在直流分量(
)处为
在上图幅值图中,取样频率为2048Hz,取样点数为2048个
上图尖峰的点对应的分别是下表
因此信号的两个cos分量的频率分别是326Hz和652Hz
他们的幅值分别是1和3
再根据找到的这两个幅值获取实部和虚部,分别为下图
则两个分量的相位均为-90°(
),复平面如下图
原信号的表达式可以表示为
快速傅里叶变换(FFT)
FFT是DFT的加速算法,所以在意义和结果的用法上和DFT完全相同
通用性
首先说明DFT和IDFT均可以使用FFT进行加速,对应的是FFT和IFFT
对于IDFT
原始公式
中的算子可以表示为
对于DFT
原始公式
其中的算子
可以设 t=n-k
则DFT与IDFT的形式得以统一
这两者对于FFT的加速过程来说没有本质区别
原理推导
以DFT为例,IDFT仅仅是在计算时更改了符号和系数而已
为了方便起见,我们让
注意:下式中的X与X(y)均是DFT输出的某一个值,如X(0),X(1)
则
之后我们根据函数的奇偶性将X分为两部分
之后我们构造2个函数
则可以知道
现在令
构造出一个单位根
因为原来的y也是一个单位根,
,且
所以我们需要将
和
均带入
并让两个结果连接起来才与原式等价
(也就是说将整个原来的式子分为了两部分,一个是
的部分,另一个是
的部分
搞到这里大多数人(
我刚学的时候) 就已经晕了,搞这玩意干啥,和DFT有啥关系?我们回想以下怎么通过X(y)这个数学上的函数算出DFT来
我们需要将k从0遍历到N-1,也就是t从N-1遍历到0,带入X(y)中,得到从X(0)到X(N-1)的这N个数
但是这样直接带入,时间复杂度和DFT没有什么区别
下面就是FFT的核心了,注意看好
将构造出来的单位根带入X(y)得
为了直观我们只看最后的结果
看出来什么了没有,这两个(前后半部分)的表达式只有一项的符号不同
也就是说,如果我们知道了
就可以同时知道
,
也就知道了DFT的计算结果了
那
怎么求呢?回看一下我们的定义
和X(y)的定义
原来如此,
原来分别是整个序列的偶数项和奇数项的DFT啊
那就可以分别对他们的奇偶数项进行DFT
以此类推,也就是 分治 的方法,或者可以叫它递归
而且输入的N必须得是2的整数次幂,不然就不能每次都分为数量相等奇偶数项
等到N==1的时候,只有一项的DFT就是它本身,直接返回即可
递归版FFT (IFFT)
根据上文所述原理,我们可以轻易写出递归版的FFT
操作流程如下:
- 判断数据数量,如果为1 则无需操作直接返回
- 将奇数项和偶数项分开
- 分别对奇数和偶数项进行FFT得出结果(递归调用)
- 将结果连接起来得到FFT
而IFFT, 是在计算
时将sin项乘上了个 -1
还需要再输出的时候将每一项均除以 N ,但是在递归里不便实现
需要的话可以在FFT结束后自行计算即可
void FFT(complex *Input, complex *Output,int Len, int inverse)
{
if (Len == 1)//长度为1则直接返回即可
return;
complex *zj_j, *zj_o, zj,zj1;
zj_j = (complex *)malloc(sizeof(complex)*Len / 2);//申请动态变量,中间变量
zj_o = (complex *)malloc(sizeof(complex)*Len / 2);
for (int i = 0; i < Len / 2; i++)//将输入的奇偶项分开
{
zj_o[i] = Input[i * 2];
zj_j[i] = Input[i * 2 + 1];
}
FFT(zj_j, zj_j, Len / 2, inverse);//对奇偶项分别进行FFT
FFT(zj_o, zj_o, Len / 2, inverse);
for (int i = 0; i < Len / 2; i++)
{
zj1.real= cos(2 * PI*i / Len);
zj1.imaginary= inverse *-sin(2 * PI*i / Len);//X2的系数
zj = complex_multiplication(zj1, zj_j[i]);//计算X2的那一项 这样可以减少一次复数乘法
Output[i] = complex_add(zj_o[i], zj);//前半部分
Output[i + Len / 2]= complex_subtraction(zj_o[i], zj);//后半部分
}
free(zj_j);//释放中间变量
free(zj_o);
}这段程序看起来非常好,也完美达到了完美的目标
但是占用内存太大了(尤其是对于单片机等设备,内存==钱啊),得优化一下
迭代版FFT
递归版FFT分析
首先我们看一下递归版FFT干了什么
我们将这种操作叫做蝴蝶操作
在同一层递归中,奇偶数项的FFT的值是确定的,而
的值是改变的
以数据量 N=8为例介绍
这图中的元素代表一层,也就是最顶层的递归
而不同颜色的中括号代表进行蝴蝶操作中使用到的不同的
他们的 奇偶数项的FFT 是相同的
并且计算后将结果放回到x(k)里面
也就是说在图中,x0-x7在经历蝴蝶变换之后就为FFT的输出数据了
而分治之后(下一层的结果)的奇偶数项的FFT已经分别存入了x0-x7
之后再看下两层递归
含义和上层相同
这便是N=8的全部层了

全家福如上
因为要先算出奇偶数项的FFT,才能进行连接(蝴蝶操作)
所以计算的顺序都是从最底层的递归开始算起
那实际上进行的操作便是
这8个输入数据分别经历了3(
)次蝴蝶操作
而如果记最底层操作为0层,向上依次为 i 层,则每次蝴蝶操作的变参数为
次单位根
如果我们知道了数据最后的排序
那只需要
分别经历以
为变参数的3次蝴蝶操作即可得出最后结果
那现在的问题就是如何得出数据最后的排序
数据排序
咱不是数学家,也不会完备的证明,所以就只说结论了
最后的序号顺序是 位逆序置换 的结果
大白话讲:将编号转化为二进制,再从高位读到低位,写的时候从低位往高位写,就是最后结果的编号
就像下表一样 (N=8)

固然可以直接按照刚才说到倒序摆放数字得出最终编号,但是某些数学家发明了更好的解决方法,可以加快运算
规律:(应该有证明,但是咱不会)
- 数据的个数
,最终编号的二进制位数是 3 (
)位
- 原始编号是偶数,最终编号最高位为0,奇数最高位为1
- 除最高位外,其他位均为 原始编号/2(向下取整) 的最终编号向右移一位的结果
(首先说明:计算按原始编号0-(N-1)进行,也就是说,再计算最终编号第x个时,我们已经知道了x/2个的最终编号是什么了)
例子:想要计算原始编号是3的最终编号,也就是第3个(从0开始数)最终编号,
最终编号最高位是1,因为原始是奇数
又因为 3/2=1(向下取整) 则第3个最终编号的低位是 第1个最终编号 向右移1位的结果(100>>1=010)
度3个最终编号是110
c语言实现
首先是计算
,因为是2的整数次幂,所以使用一个循环即可
之后建立一个最终编号的数组 rev ,并按照上文提到规律进行计算
int lim = 1,//用于计数的中间变量
len = 0, //最终编号的二进制位数
*rev;//最终编号
rev = (int *)malloc(sizeof(int)*Len);
rev[0] = 0;
while (lim < Len)//计算log 获取最终编号的二进制位数
{
lim <<= 1;
len++;
}
for (int i = 0; i < lim; i++)//获取最终编号
{
rev[i] = (rev[i >> 1] >> 1) | ((i & 1) << (len - 1));
}实现
首先是将输入数组按照最终编号排序
之后需要一个循环来扫描单位根(在例子中是2,4,8次单位根)
在之前这个循环中需要嵌套一个循环,它是用于扫描n次单位根第几个的(如
)
在这个循环中还需嵌套一个循环,用于扫描左半得出全部答案(如
单位根时,要扫描
得出
的答案)
为了减少几次三角运算,我们要用 单位根性质5(数学基础中的)
来通过
进行复数乘法计算出
void FFT(complex *Input, complex *Output, int Len, int inverse)
{
complex zj,omega,zj1,zj2;
int lim = 1,//用于计数的中间变量
len = 0, //最终编号的二进制位数
*rev;//最终编号
rev = (int *)malloc(sizeof(int)*Len);
rev[0] = 0;
while (lim < Len)//计算log 获取最终编号的二进制位数
{
lim <<= 1;
len++;
}
for (int i = 0; i < Len; i++)//获取最终编号并将输入按照最终编号顺序排列
{
rev[i] = (rev[i >> 1] >> 1) | ((i & 1) << (len - 1));
Output[i] = Input[rev[i]];
}
for (int m = 1; m < Len; m *= 2)//单位根扫描
{
zj.real = cos(PI / m);//本来应该是2PI/2m 进行了约分
zj.imaginary = inverse *-sin(PI / m);
for (int i = 0; i < Len; i += m * 2)//扫描奇偶项
{
omega.real = 1;
omega.imaginary = 0;
for (int j = 0; j < m; j++)//扫描左半
{
zj1 = Output[i + j];
zj2 = complex_multiplication(omega, Output[i + j + m]);
Output[i + j] = complex_add(zj1,zj2);
Output[i + j + m] = complex_subtraction(zj1, zj2);//蝴蝶操作,同时得出左右半
omega = complex_multiplication(omega, zj);//更新单位根
}
}
}
if (inverse == -1)//IFFT时需要/N
{
for (int i = 0; i < Len; i++)
{
Output[i].real /= Len;
Output[i].imaginary /= Len;
}
}
}


成品
FFT的内容就到这了,下面给出完整代码
使用FFT的结果作为信号分析时的方法请看 DFT的结果含义
(使用目录跳转即可)
#define PI (3.1415926)
typedef struct __complex
{
float real;
float imaginary;
}complex;
complex complex_multiplication(complex a, complex b)
{
complex zj;
zj.real = a.real*b.real - a.imaginary*b.imaginary;
zj.imaginary = a.real*b.imaginary + a.imaginary*b.real;
return zj;
}
complex complex_add(complex a, complex b)
{
complex zj;
zj.real = a.real + b.real;
zj.imaginary = a.imaginary + b.imaginary;
return zj;
}
complex complex_subtraction(complex a, complex b)
{
complex zj;
zj.real = a.real - b.real;
zj.imaginary = a.imaginary - b.imaginary;
return zj;
}
//输入输出的数组指针,长度只能是2的整数次幂,inverse为1是FFT,-1是IFFT
void FFT(complex *Input, complex *Output, int Len, int inverse)
{
complex zj,omega,zj1,zj2;
int lim = 1,//用于计数的中间变量
len = 0, //最终编号的二进制位数
*rev;//最终编号
rev = (int *)malloc(sizeof(int)*Len);
rev[0] = 0;
while (lim < Len)//计算log 获取最终编号的二进制位数
{
lim <<= 1;
len++;
}
for (int i = 0; i < Len; i++)//获取最终编号并将输入按照最终编号顺序排列
{
rev[i] = (rev[i >> 1] >> 1) | ((i & 1) << (len - 1));
Output[i] = Input[rev[i]];
}
for (int m = 1; m < Len; m *= 2)//单位根扫描
{
zj.real = cos(PI / m);//本来应该是2PI/2m 进行了约分
zj.imaginary = inverse *-sin(PI / m);
for (int i = 0; i < Len; i += m * 2)//扫描奇偶项
{
omega.real = 1;
omega.imaginary = 0;
for (int j = 0; j < m; j++)//扫描左半
{
zj1 = Output[i + j];
zj2 = complex_multiplication(omega, Output[i + j + m]);
Output[i + j] = complex_add(zj1,zj2);
Output[i + j + m] = complex_subtraction(zj1, zj2);//蝴蝶操作,同时得出左右半
omega = complex_multiplication(omega, zj);//更新单位根
}
}
}
if (inverse == -1)//IFFT时需要/N
{
for (int i = 0; i < Len; i++)
{
Output[i].real /= Len;
Output[i].imaginary /= Len;
}
}
}另外:不知道为什么,网上的FFT的单位根的 sin 使用的都是正值但是我根据公式推出的和计算相位角所得到的都应该是 -sin
请大佬解答






























 1万+
1万+

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








