11.BP神经网络算法概念理解数学建模机器学习

alwaysuzybai

已于 2022-09-24 11:15:00 修改

阅读量1k

点赞数 1

分类专栏：机器学习

于 2022-09-24 11:08:19 首次发布

本文链接：https://blog.csdn.net/m0_57656758/article/details/126346958

版权

机器学习专栏收录该内容

35 篇文章 7 订阅

订阅专栏

不是所有的函数都满足一一映射的关系，无法表示函数关系，故引入BP

“分类”是神经网络的一大应用，使用神经网络完成分类任务

零基础入门深度学习（1）- 感知器/神经元

0.前言

1.背景

2.多层前馈网络神经（Multilayer-Feed-Foraward Neural Network）

2.1Back Propagation算法被使用在多层前馈网络神经上

2.2多层前馈神经网络由以下部分组成（如下图）：

2.2.1输入层（input layer）

2.2.2从输入层到隐藏层

2.2.3隐藏层（hidden layer）

2.2.4从隐藏层到输出层

2.2.5输出层（output layer）

0.前言

优势：一个仅有一个隐藏层的浅层神经网络就能拟合任何一个函数，但是它需要很多很多个神经元；而深层神经网络用很少的神经元就能拟合同样的函数，即深层网络表达能力更强。想要拟合一个函数，要么使用是一个浅而宽的网络，要么使用深而窄的网络，显然后者更节省资源。

深层网络也有劣势，就是它不太容易训练，需要更大量的数据和更深层的技巧！

1.背景

a.以人脑中的神经网络为启发

b.最著名的算法是1990年的Back Propagation算法

2.多层前馈网络神经（Multilayer-Feed-Foraward Neural Network）

2.1Back Propagation算法被使用在多层前馈网络神经上

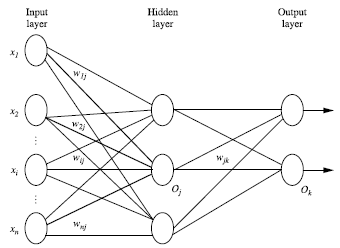
2.2多层前馈神经网络由以下部分组成（如下图）：

这里写图片描述

2.2.1输入层（input layer）

元素维度与输入量的特征息息相关，输入层是由训练集的实例特征向量传入，这层负责接收输入数据；

2.2.2从输入层到隐藏层

连接输入层和隐藏层的是 $\omega_{ 1}$ 和 $b_{1}$ 。由X计算到H，就是矩阵运算：

$H= X*\omega _{1}+b_{1}$

如上式所示：在设定隐藏层为50维（也可以理解成50个神经元）之后，矩阵H的大小为1*50的矩阵。

2.2.3隐藏层（hidden layer）

输入层和输出层之间的层叫做隐藏层；

2.2.4从隐藏层到输出层

连接隐藏层和输出层的是 $\omega _{2}$ 和 $b_{2}$ ，通过矩阵运算得：

$Y= H*\omega _{2}+b_{2}$

2.2.5输出层（output layer）

可以从输出层获取神经网络输出数据；

每层由单元（unit）组成，层与层之间的神经元有连接，而层内之间的神经元没有连接。

通过上述两个线性方程的计算，我们就能得到最终的输出Y了，一系列线性方程的运算最终都可以用一个线性方程表示。也就是说，上述两个式子联立后可以用一个线性方程表达。对于两次神经网络是这样，就算网络深度增加到100层，也依然是这样。但这样的话神经网络就失去了意义。（隐藏层比较多【大于2】的神经网络叫做深度神经网络；而深度学习，就是使用深层架构【比如，深度神经网络】的机器学习方法。）

2.3BP神经网络的拓扑结构：

在这里插入图片描述

所以这里要对神经网络注入灵魂：激活层。

3.单个神经元 /感知器

在这里插入图片描述

3.1感知器定义

3.1.1输入权重

$x_{i}$ 为输入， $\omega _{i}$ 代表权重， $\theta _{i}$ 代表阈值（阈值又叫临界值，是指一个效应能够产生的最低值或最高值）。 $y_{k}$ 代表输出。还有偏置b和激活函数f(x)没有画出。总之，一个神经元需要四个参数和一个函数才能得到输出（输入 $x_{i}$ 、权重 $\omega _{i}$ 、阈值 $\theta _{i}$ 、偏置 $b$ ➕激活函数 $f(x)$ ）

具体数学表达为：

$net_{i}=\sum_{I=1}^{n}X_{i}W_{i}=X_{1}W_{1}+X_{2}W_{2}+\cdot \cdot \cdot$

如果 $net_{i}$ 大于 $\theta _{i}$ ，那么这个神经元被激活，继续运算；

反之神经元关闭，没有输出。

3.1.2输出

激活后做以下运算：

$Y_{k}$ =f( $net_{i}$ +b)，得到这个神经元的输出。

3.2激活层

简言之，激活层是为矩阵运算的结果添加非线性的。

3.3激活函数f(x)

在单个神经元中的f(x)是激活函数。

阶跃函数：当输入小于等于0时，输出0；当输入大于0时，输出1

3.3.1为什么要使用激活函数？

激活函数给神经元引入了非线性因素，使得神经网络可以任意逼近任何非线性函数，这样神经网络就可以应用到众多的非线性模型中。

如果没有激活函数，无论网络有多少层，输出都只能是输入的线性组合，这样就形成了原始的感知机。

3.4感知机

我们在学深度学习的时候，最早接触的神经网络应该属于感知器（感知器本身就是一个很简单的神经网络，也许有人认为它不属于神经网络，当然认为它和神经网络长得像也行）。

要想激活这个感知器，使得y=1，就必须使x1*w1 + x2*w2 +....+xn*wn > θ （θ 为一个阈值），而θ 越大，想激活这个感知器的难度越大，人工选择一个阈值并不是一个好的方法，因为样本那么多，我不可能手动选择一个阈值，使得模型整体表现最佳，那么我们可以使得θ 变成可学习的，这样一来，θ 会自动学习到一个数，使得模型的整体表现最佳。当把θ 移动到左边，它就成了偏置，x1*w1 + x2*w2 +....+xn*wn - θ > 0 ----->x*w +b > 0，总之，偏置的大小控制着激活这个感知器的难易程度。

4.感知器的训练

4.1权重项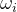 $\omega _{i}$ 和偏置项b如何获得？

使用感知器训练算法！

将权重项 $\omega _{i}$ 和偏置项b赋初值为0，利用感知器规则迭代修改 $\omega _{i}$ 和b，直到训练完成。

$\omega _{i}\leftarrow \omega _{i}+\Delta \omega _{i}$

$b\leftarrow b+\Delta b$

（上式联想文章：lMS算法推导LMS算法公式推导_睡觉特早头发特多的博客-CSDN博客）

其中：

$\Delta \omega _{i}= \eta (t-y)x_{i}$

$\Delta b=\eta (t-y)$

$\omega _{i}$ 是与输入 $x _{i}$ 对应的权重项， $b$ 是偏置项。事实上，可以把 $b$ 看作是值永远为1的输入 $x_{b}$ 所对应的权值。 $t$ 是训练样本的实际值，一般称之为label；而 $y$ 是感知器的输出值，它是根据目标/预测函数计算得到的； $\eta$ 是一个称为学习速率的常数，其作用是控制每一步调整权的幅度。

每次从训练数据中取出一个样本的输入向量 $x$ ，使用感知器计算其输出 $y$ ，再根据上面的规则来调整权重。每处理一个样本就调整一次权重。经过多轮迭代后（即全部的训练数据被反复处理多轮），就可以训练出感知器的权重，使之实现目标函数。

5.什么是BP神经网络？

用于寻找数据集中非线性的、复杂的数据关系。它是基于生物神经网络的原型，对其进行抽象和模拟，模仿人脑思考问题的方式和方法，能很好的去发掘数据之间的相关性。其主要用于数据的建模和预测。

5.1反向传播的理解

BP（Back-propagation，反向传播）神经网络是最传统的神经网络。当下的各种神经网络的模型可以看作是BP神经网络的变种。BP神经网络称呼由两部分组成，BP（反向传播）和神经网络。神经网络是说这种算法是模拟大脑神经元的工作机理，并由多层神经元构成的网络。

反向传播！将预测值与真实值进行对比，然后给出一个评价，这个过程就是反向传播。神经网络也是类似的过程，通过网络的超参数进行随机配置，得到一个预测值，这是一个正向传播的过程。而后计算出预测值与真实值的差距，根据这个差距相应调整参数，这是一个反向传播的过程。通过多次迭代，循环往复，我们就能计算出一组合适的参数，得到的网络模型就能拟合一个我们未知的复杂函数。

BP神经网络示意图：