图片特征提取整理

>w(x,y)是窗口函数，最简单情形就是窗口内的所有像素所对应的w权重系数均为1。但有时候，我们会将w(x,y)函数设定为以窗口中心为原点的二元正态分布。如果窗口中心点是角点时，移动前与移动后，该点的灰度变化应该最为剧烈，所以该点权重系数可以设定大些，表示窗口移动时，该点在灰度变化贡献较大；而离窗口中心(角点)较远的点，这些点的灰度变化几近平缓，这些点的权重系数，可以设定小点，以示该点对灰度变化贡献较小，那么我们自然想到使用二元高斯函数来表示窗口函数，这里仅是个人理解，大家可以参考下。

根据上述表达式，当窗口处在平坦区域上滑动，可以想象的到，灰度不会发生变化，那么E(u,v) = 0；如果窗口处在比纹理比较丰富的区域上滑动，那么灰度变化会很大。算法最终思想就是计算灰度发生较大变化时所对应的位置，当然这个较大是指针任意方向上的滑动，并非单指某个方向。

4.E(u,v)表达式进一步演化

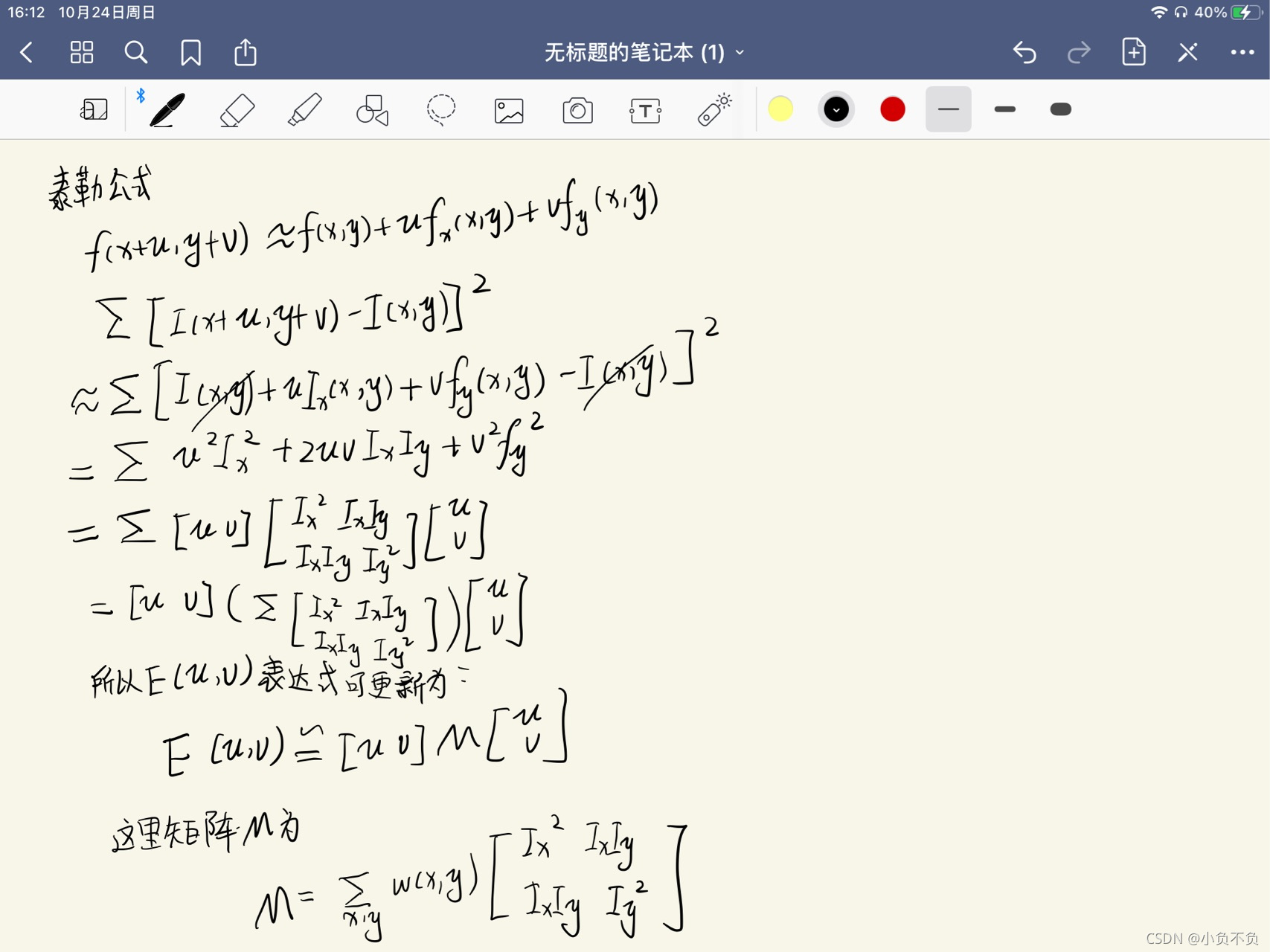
椭圆函数特征值与图像中的角点、直线（边缘）和平面之间的关系如下图所示。共可分为三种情况：

图像中的直线。一个特征值大，另一个特征值小，λ1≫λ2λ1≫λ2或λ2≫λ1λ2≫λ1。自相关函数值在某一方向上大，在其他方向上小。
图像中的平面。两个特征值都小，且近似相等；自相关函数数值在各个方向上都小。
图像中的角点。两个特征值都大，且近似相等，自相关函数在所有方向都增大。

矩阵M的关键性

难道我们是直接求上述的E(u,v)值来判断角点吗？Harris角点检测并没有这样做，而是通过对窗口内的每个像素的x方向上的梯度与y方向上的梯度进行统计分析。这里以Ix和Iy为坐标轴，因此每个像素的梯度坐标可以表示成(Ix,Iy)。针对平坦区域，边缘区域以及角点区域三种情形进行分析：

下图是对这三种情况窗口中的对应像素的梯度分布进行绘制

如果使用椭圆进行数据集表示，则绘制图示如下

不知道大家有没有注意到这三种区域的特点，平坦区域上的每个像素点所对应的(IX,IY)坐标分布在原点附近，其实也很好理解，针对平坦区域的像素点，他们的梯度方向虽然各异，但是其幅值都不是很大，所以均聚集在原点附近；边缘区域有一坐标轴分布较散，至于是哪一个坐标上的数据分布较散不能一概而论，这要视边缘在图像上的具体位置而定，如果边缘是水平或者垂直方向，那么Iy轴方向或者Ix方向上的数据分布就比较散；角点区域的x、y方向上的梯度分布都比较散。我们是不是可以根据这些特征来判断哪些区域存在角点呢？

虽然我们利用E(u,v)来描述角点的基本思想，然而最终我们仅仅使用的是矩阵M。让我们看看矩阵M形式，是不是跟协方差矩阵形式很像，像归像，但是还是有些不同，哪儿不同？一般协方差矩阵对应维的随机变量需要减去该维随机变量的均值，但矩阵M中并没有这样做，所以在矩阵M里，我们先进行各维的均值化处理，那么各维所对应的随机变量的均值为0，协方差矩阵就大大简化了，简化的最终结果就是矩阵M，是否明白了？我们的目的是分析数据的主要成分，相信了解PCA原理的，应该都了解均值化的作用。

如果我们对协方差矩阵M进行对角化，很明显，特征值就是主分量上的方差，这点大家应该明白吧？不明白的话可以复习下PCA原理。如果存在两个主分量所对应的特征值都比较大，说明什么？像素点的梯度分布比较散，梯度变化程度比较大，符合角点在窗口区域的特点；如果是平坦区域，那么像素点的梯度所构成的点集比较集中在原点附近，因为窗口区域内的像素点的梯度幅值非常小，此时矩阵M的对角化的两个特征值比较小；如果是边缘区域，在计算像素点的x、y方向上的梯度时，边缘上的像素点的某个方向的梯度幅值变化比较明显，另一个方向上的梯度幅值变化较弱，其余部分的点都还是集中原点附近，这样M对角化后的两个特征值理论应该是一个比较大，一个比较小，当然对于边缘这种情况，可能是呈45°的边缘，致使计算出的特征值并不是都特别的大，总之跟含有角点的窗口的分布情况还是不同的。

因此可以得出下列结论：

>特征值都比较大时，即窗口中含有角点

>特征值一个较大，一个较小，窗口中含有边缘

>特征值都比较小，窗口处在平坦区域

Harris角点算法实现

其中k是常量，一般取值为0.04~0.06，这个参数仅仅是这个函数的一个系数，它的存在只是调节函数的形状而已。

但是为什么会使用这样的表达式呢？一下子是不是感觉很难理解？其实也不难理解，函数表达式一旦出来，我们就可以绘制它的图像，而这个函数图形正好满足上面几个区域的特征。通过绘制函数图像，直观上更能理解。绘制的R函数图像如下：

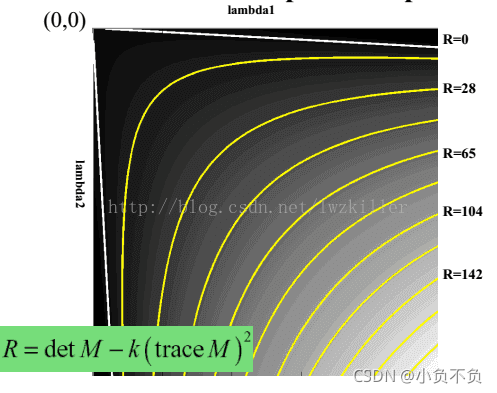
Harris角点的性质

由此，可以得出这样的结论：增大αα的值，将减小角点响应值RR，降低角点检测的灵性，减少被检测角点的数量；减小αα值，将增大角点响应值RR，增加角点检测的灵敏性，增加被检测角点的数量。

2. Harris角点检测算子对亮度和对比度的变化不敏感

这是因为在进行Harris角点检测时，使用了微分算子对图像进行微分运算，而微分运算对图像密度的拉升或收缩和对亮度的抬高或下降不敏感。换言之，对亮度和对比度的仿射变换并不改变Harris响应的极值点出现的位置，但是，由于阈值的选择，可能会影响角点检测的数量。

3. Harris角点检测算子具有旋转不变性

Harris角点检测算子使用的是角点附近的区域灰度二阶矩矩阵。而二阶矩矩阵可以表示成一个椭圆，椭圆的长短轴正是二阶矩矩阵特征值平方根的倒数。当特征椭圆转动时，特征值并不发生变化，所以判断角点响应值RR也不发生变化，由此说明Harris角点检测算子具有旋转不变性。

4. Harris角点检测算子不具有尺度不变性

如下图所示，当右图被缩小时，在检测窗口尺寸不变的前提下，在窗口内所包含图像的内容是完全不同的。左侧的图像可能被检测为边缘或曲线，而右侧的图像则可能被检测为一个角点

参考文章：Harris角点检测原理详解_lwzkiller的专栏-CSDN博客_harris角点检测

census变换

Census 变换在实际场景中,造成亮度差异的原因有很多,如由于左右摄像机不同的视角接受到的光强不一致,摄像机增益、电平可能存在差异,以及图像采集不同通道的噪声不同等，cencus方法保留了窗口中像素的位置特征,并且对亮度偏差较为鲁棒,简单讲就是能够减少光照差异引起的误匹配。

实现原理：在视图中选取任一点，以该点为中心划出一个例如3 × 3 的矩形，矩形中除中心点之外的每一点都与中心点进行比较，灰度值小于中心点即记为1，灰度大于中心点的则记为0，以所得长度为 8 的只有 0 和 1 的序列作为该中心点的 census 序列,即中心像素的灰度值被census 序列替换。经过census变换后的图像使用汉明距离计算相似度,所谓图像匹配就是在视差图中找出与参考像素点相似度最高的点，而汉明距正是视差图像素与参考像素相似度的度量。具体而言，对于欲求取视差的左右视图，要比较两个视图中两点的相似度，可将此两点的census值逐位进行异或运算，然后计算结果为1 的个数，记为此两点之间的汉明值，汉明值是两点间相似度的一种体现，汉明值愈小，两点相似度愈大实现算法时先异或再统计1的个数即可，汉明距越小即相似度越高。（尽管census变换提高了匹配鲁棒性,但其包含的图像信息有限,原始灰度信息己经完全被抛弃了,因此不能将变换结果用于单像素或较小窗口的匹配,仍需要使用与其他区域匹配方法中类似的匹配窗口）变换过程如下所示。

susan角点检测算法

SUSAN算法是1997年牛津大学的Smith等人提出的一种处理灰度图像的方法,它主要是用来计算图像中的角点特征。SUSAN算法选用圆形模板(如图1所示)。将位于圆形窗口模板中心等待检测的像素点称为核心点。核心点的邻域被划分为两个区域:亮度值相似于核心点亮度的区域即核值相似区(Univalue SegmentAs-similatingNueleus,USAN)和亮度值不相似于核心点亮度的区域。

USAN的典型区域如图2所示。模板在图像上移动时,当圆形模板完全在背景或者目标区域时，其USAN区域最大,如图2(a)；当核心在边缘时,USAN区域减少一半,如图2(c)；当核心在角点时, USAN区域最小，如图2(d)。基于这一原理, Smith提出了最小核值相似区角点检测算法。

SUSAN角点检测算法的具体步骤如下:

(1)在图像上放置一个37个像素的圆形模板，模板在图像上滑动，依次比较模板内各个像素点的灰度与模板核的灰度，判断是否属于USAN区域。判别函数如下：

(2)统计圆形模板中和核心点有相似亮度值的像素个数n(r0)。

其中，D(r0)是以r0为中心的圆形模板区域

(3)使用如下角点响应函数。若某个像素点的USAN值小于某一特定阈值，则该点被认为是初始角点，其中，g可以设定为USAN的最大面积的一半。

(4)对初始角点进行非极值抑制来求得最后的角点。
参考文章：https://blog.csdn.net/u013989576/article/details/49226611

LBP算法

LBP（Local Binary Pattern，局部二值模式）是一种用来描述图像局部纹理特征的算子；它具有旋转不变性和灰度不变性等显著的优点。它是首先由T. Ojala, M.Pietikäinen, 和D. Harwood 在1994年提出，用于纹理特征提取。而且，提取的特征是图像的局部的纹理特征；

1、LBP特征的描述

原始的LBP算子定义为在3*3的窗口内，以窗口中心像素为阈值，将相邻的8个像素的灰度值与其进行比较，若周围像素值大于中心像素值，则该像素点的位置被标记为1，否则为0。这样，3*3邻域内的8个点经比较可产生8位二进制数（通常转换为十进制数即LBP码，共256种），即得到该窗口中心像素点的LBP值，并用这个值来反映该区域的纹理信息。如下图所示：

LBP的改进版本：

原始的LBP提出后，研究人员不断对其提出了各种改进和优化。

（1）圆形LBP算子：

基本的 LBP 算子的最大缺陷在于它只覆盖了一个固定半径范围内的小区域，这显然不能满足不同尺寸和频率纹理的需要。为了适应不同尺度的纹理特征，并达到灰度和旋转不变性的要求，Ojala 等对 LBP 算子进行了改进，将 3×3 邻域扩展到任意邻域，并用圆形邻域代替了正方形邻域，改进后的 LBP 算子允许在半径为 R 的圆形邻域内有任意多个像素点。从而得到了诸如半径为R的圆形区域内含有P个采样点的LBP算子；

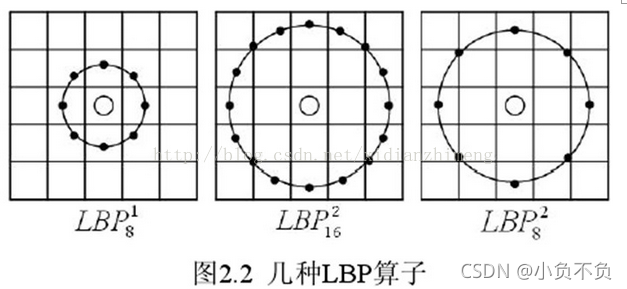
（2）LBP旋转不变模式

从 LBP 的定义可以看出，LBP 算子是灰度不变的，但却不是旋转不变的。图像的旋转就会得到不同的 LBP值。

Maenpaa等人又将 LBP 算子进行了扩展，提出了具有旋转不变性的 LBP 算子，即不断旋转圆形邻域得到一系列初始定义的 LBP 值，取其最小值作为该邻域的 LBP 值。

图 2.5 给出了求取旋转不变的 LBP 的过程示意图，图中算子下方的数字表示该算子对应的 LBP 值，图中所示的 8 种 LBP模式，经过旋转不变的处理，最终得到的具有旋转不变性的 LBP 值为 15。也就是说，图中的 8 种 LBP 模式对应的旋转不变的 LBP 模式都是00001111。

（3）LBP等价模式

一个LBP算子可以产生不同的二进制模式，对于半径为R的圆形区域内含有P个采样点的LBP算子将会产生P2 种模式。很显然，随着邻域集内采样点数的增加，二进制模式的种类是急剧增加的。例如：5×5邻域内20个采样点，有220＝1,048,576种二进制模式。如此多的二值模式无论对于纹理的提取还是对于纹理的识别、分类及信息的存取都是不利的。同时，过多的模式种类对于纹理的表达是不利的。例如，将LBP算子用于纹理分类或人脸识别时，常采用LBP模式的统计直方图来表达图像的信息，而较多的模式种类将使得数据量过大，且直方图过于稀疏。因此，需要对原始的LBP模式进行降维，使得数据量减少的情况下能最好的代表图像的信息。

为了解决二进制模式过多的问题，提高统计性，Ojala提出了采用一种“等价模式”（Uniform Pattern）来对LBP算子的模式种类进行降维。Ojala等认为，在实际图像中，绝大多数LBP模式最多只包含两次从1到0或从0到1的跳变。因此，Ojala将“等价模式”定义为：当某个LBP所对应的循环二进制数从0到1或从1到0最多有两次跳变时，该LBP所对应的二进制就称为一个等价模式类。如00000000（0次跳变），00000111（只含一次从0到1的跳变），10001111（先由1跳到0，再由0跳到1，共两次跳变）都是等价模式类。除等价模式类以外的模式都归为另一类，称为混合模式类，例如10010111（共四次跳变）（这是我的个人理解，不知道对不对）。

通过这样的改进，二进制模式的种类大大减少，而不会丢失任何信息。模式数量由原来的2P种减少为 P ( P-1)+2种，其中P表示邻域集内的采样点数。对于3×3邻域内8个采样点来说，二进制模式由原始的256种减少为58种，这使得特征向量的维数更少，并且可以减少高频噪声带来的影响。

2、LBP特征用于检测的原理

显而易见的是，上述提取的LBP算子在每个像素点都可以得到一个LBP“编码”，那么，对一幅图像（记录的是每个像素点的灰度值）提取其原始的LBP算子之后，得到的原始LBP特征依然是“一幅图片”（记录的是每个像素点的LBP值）。

从上图可以看出LBP对光照具有很强的鲁棒性

LBP的应用中，如纹理分类、人脸分析等，一般都不将LBP图谱作为特征向量用于分类识别，而是采用LBP特征谱的统计直方图作为特征向量用于分类识别。

因为，从上面的分析我们可以看出，这个“特征”跟位置信息是紧密相关的。直接对两幅图片提取这种“特征”，并进行判别分析的话，会因为“位置没有对准”而产生很大的误差。后来，研究人员发现，可以将一幅图片划分为若干的子区域，对每个子区域内的每个像素点都提取LBP特征，然后，在每个子区域内建立LBP特征的统计直方图。如此一来，每个子区域，就可以用一个统计直方图来进行描述；整个图片就由若干个统计直方图组成；

例如：一幅100*100像素大小的图片，划分为10*10=100个子区域（可以通过多种方式来划分区域），每个子区域的大小为10*10像素；在每个子区域内的每个像素点，提取其LBP特征，然后，建立统计直方图；这样，这幅图片就有10*10个子区域，也就有了10*10个统计直方图，利用这10*10个统计直方图，就可以描述这幅图片了。之后，我们利用各种相似性度量函数，就可以判断两幅图像之间的相似性了；

3、对LBP特征向量进行提取的步骤

（1）首先将检测窗口划分为16×16的小区域（cell）；

（2）对于每个cell中的一个像素，将相邻的8个像素的灰度值与其进行比较，若周围像素值大于中心像素值，则该像素点的位置被标记为1，否则为0。这样，3*3邻域内的8个点经比较可产生8位二进制数，即得到该窗口中心像素点的LBP值；

（3）然后计算每个cell的直方图，即每个数字（假定是十进制数LBP值）出现的频率；然后对该直方图进行归一化处理。

（4）最后将得到的每个cell的统计直方图进行连接成为一个特征向量，也就是整幅图的LBP纹理特征向量；

然后便可利用SVM或者其他机器学习算法进行分类了。

Reference：

黄非非，基于 LBP 的人脸识别研究，重庆大学硕士学位论文，2009.5

https://blog.csdn.net/xidianzhimeng/article/details/19634573

HOG特征

方向梯度直方图（Histogram of Oriented Gradient, HOG）特征是一种在计算机视觉和图像处理中用来进行物体检测的特征描述子。它通过计算和统计图像局部区域的梯度方向直方图来构成特征。Hog特征结合SVM分类器已经被广泛应用于图像识别中，尤其在行人检测中获得了极大的成功。需要提醒的是，HOG+SVM进行行人检测的方法是法国研究人员Dalal在2005的CVPR上提出的，而如今虽然有很多行人检测算法不断提出，但基本都是以HOG+SVM的思路为主。

（1）主要思想：

在一副图像中，局部目标的表象和形状（appearance and shape）能够被梯度或边缘的方向密度分布很好地描述。（本质：梯度的统计信息，而梯度主要存在于边缘的地方）。

（2）具体的实现方法是：

首先将图像分成小的连通区域，我们把它叫细胞单元。然后采集细胞单元中各像素点的梯度的或边缘的方向直方图。最后把这些直方图组合起来就可以构成特征描述器。

（3）提高性能：

把这些局部直方图在图像的更大的范围内（我们把它叫区间或block）进行对比度归一化（contrast-normalized），所采用的方法是：先计算各直方图在这个区间（block）中的密度，然后根据这个密度对区间中的各个细胞单元做归一化。通过这个归一化后，能对光照变化和阴影获得更好的效果。

（4）优点：

与其他的特征描述方法相比，HOG有很多优点。首先，由于HOG是在图像的局部方格单元上操作，所以它对图像几何的和光学的形变都能保持很好的不变性，这两种形变只会出现在更大的空间领域上。其次，在粗的空域抽样、精细的方向抽样以及较强的局部光学归一化等条件下，只要行人大体上能够保持直立的姿势，可以容许行人有一些细微的肢体动作，这些细微的动作可以被忽略而不影响检测效果。因此HOG特征是特别适合于做图像中的人体检测的。

算法流程图

HOG特征提取方法就是将一个image（你要检测的目标或者扫描窗口）：

1）灰度化（将图像看做一个x,y,z（灰度）的三维图像）；

2）采用Gamma校正法对输入图像进行颜色空间的标准化（归一化）；目的是调节图像的对比度，降低图像局部的阴影和光照变化所造成的影响，同时可以抑制噪音的干扰；

3）计算图像每个像素的梯度（包括大小和方向）；主要是为了捕获轮廓信息，同时进一步弱化光照的干扰。

4）将图像划分成小cells（例如8*8像素/cell）；

5）统计每个cell的梯度直方图（不同梯度的个数），即可形成每个cell的descriptor；

6）将每几个cell组成一个block（例如3*3个cell/block），一个block内所有cell的特征descriptor串联起来便得到该block的HOG特征descriptor。

7）将图像image内的所有block的HOG特征descriptor串联起来就可以得到该image（你要检测的目标）的HOG特征descriptor了。这个就是最终的可供分类使用的特征向量了。

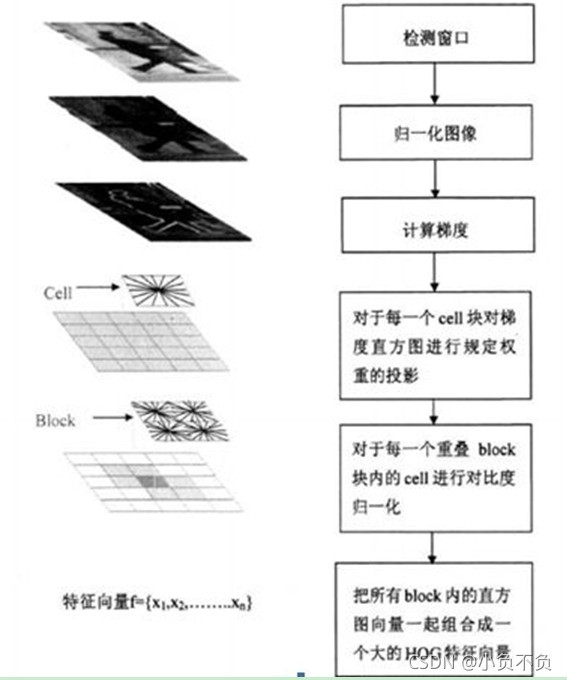
具体每一步的详细过程如下：

（1）标准化gamma空间和颜色空间

为了减少光照因素的影响，首先需要将整个图像进行规范化（归一化）。在图像的纹理强度中，局部的表层曝光贡献的比重较大，所以，这种压缩处理能够有效地降低图像局部的阴影和光照变化。因为颜色信息作用不大，通常先转化为灰度图；

(2) 而梯度可分解为 x 方向的梯度 G{x} 和 y 方向的梯度 G{y} 。

某个像素点的 x 方向的梯度的计算可以通过这个像素点左右两边的像素值的差值的绝对值计算出来，而 y 方向的梯度可以通过该像素点上下两边的像素值的差值的绝对值计算。而根据下面的两个公式可以计算每一个像素点的梯度方向和梯度幅值。

最常用的方法是：首先用[-1,0,1]梯度算子对原图像做卷积运算，得到x方向（水平方向，以向右为正方向）的梯度分量gradscalx，然后用[1,0,-1]T梯度算子对原图像做卷积运算，得到y方向（竖直方向，以向上为正方向）的梯度分量gradscaly。然后再用以上公式计算该像素点的梯度大小和方向。

（3）为每个细胞单元构建梯度方向直方图

第三步的目的是为局部图像区域提供一个编码，同时能够保持对图像中人体对象的姿势和外观的弱敏感性。

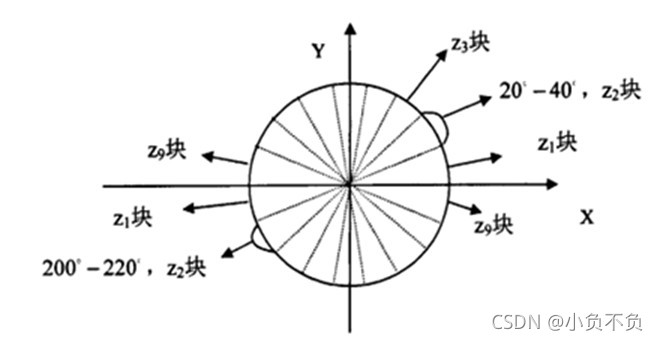
我们将图像分成若干个“单元格cell”，例如每个cell为8*8个像素。假设我们采用9个bin的直方图来统计这8*8个像素的梯度信息。也就是将cell的梯度方向360度分成9个方向块，如图所示：例如：如果这个像素的梯度方向是20-40度，直方图第2个bin的计数就加一，这样，对cell内每个像素用梯度方向在直方图中进行加权投影（映射到固定的角度范围），就可以得到这个cell的梯度方向直方图了，就是该cell对应的9维特征向量（因为有9个bin）。

像素梯度方向用到了，那么梯度大小呢？梯度大小就是作为投影的权值的。例如说：这个像素的梯度方向是20-40度，然后它的梯度大小是2（假设啊），那么直方图第2个bin的计数就不是加一了，而是加二（假设啊）。

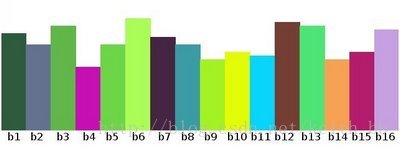
HOG是通过上面公式计算出来的梯度方向的角度是一个范围在0-360度的弧度值，为了计算简单，将梯度向的范围约束为0-180度，并且分割为9个方向，每个方向20度，再将约束后的角度除以20，则现在的梯度方向角度值就变为范围在[0,9)。

细胞单元可以是矩形的（rectangular），也可以是星形的（radial）。

3.cell、block、windowsSize、stride的关系。

上图中单个cell的为8X8个像素，把cell对应的方向直方图转换为单维向量，按规定组距对对应方向梯度个数进行编码，得到单个cell的9个特征，每个block包含2X2个cell,那么每个block包含2X2个cell也就是2X2X9=36个特征，而每个block移动（stride）这里选择overlap，就是为2分之一重叠，一个64X128大小的图像横着有15个block,坚着有7个，最后得到的特征数为36X7X15=3780维。

参考文章：https://blog.csdn.net/matt45m/article/details/85325897

https://blog.csdn.net/zouxy09/article/details/7929348

FAST角点检测

1、在图像中任选一点p，假定其像素（亮度）值为 Ip

2、以3为半径画圆，覆盖p点周围的16个像素，如下图所示

3、设定阈值t，如果这周围的16个像素中有连续的n个像素的像素值都小于 Ip−t或者有连续的n个像素都大于Ip+t，那么这个点就被判断为角点。在OpenCV的实现中n取值为12（16个像素周长的 3/4）.

4、一种更加快的改进是：首先检测p点周围的四个点，即1， 5， 9， 12四个点中是否有三个点满足超过Ip+t，如果不满足，则直接跳过，如果满足，则继续使用前面的算法，全部判断16个点中是否有12个满足条件。

以上算法的缺点：很可能大部分检测出来的点彼此之间相邻，我们要去除一部分这样的点。为了解决这一问题，我们采用了非极大值抑制的算法

非极大值抑制
对一个角点P建立一个3*3（或5*5，7*7）的窗口，如果该窗口内出现了另一个角点Q，则比较P与Q的大小，如果P大，则将Q点删除，如果P小，则将P点删除。

1、在速度上要比其他算法速度快很多

2、受图像噪声以及设定的阈值影响很大

3、FAST不产生多尺度特征而且FAST特征点没有方向信息，这样就会失去旋转不变性

2、opencv-Fast角点检测算法C++版代码

#include <QCoreApplication>  //该行为Qt环境使用。VS下请注释或删除该行。
#include <opencv2/opencv.hpp>

using namespace cv;
using namespace std;

//**********************************************************************************************
//                                     【fast角点检测算法】
//**********************************************************************************************

int main()
{
    string path = "/home/jason/1.jpg";  //图片路径
    cv::Mat img, gray;

    img = cv::imread(path);  //读取图片
    cv::cvtColor(img, gray, cv::COLOR_BGR2GRAY);  //转换为灰度图
    std::vector<KeyPoint> kp;  //特征点向量

    cv::FastFeatureDetector fast(32);  //FAST特征检测器， 32为阈值，阈值越大，特征点越少
    fast.detect(gray, kp);  //检测fast特征点

    cv::drawKeypoints(img, kp, img, cv::Scalar(0, 255, 0), cv::DrawMatchesFlags::DRAW_OVER_OUTIMG);  //画特征点

    cv::namedWindow("img", cv::WINDOW_NORMAL);
    cv::imshow("img", img);
    cv::waitKey(0);

    cv::imwrite("/home/jason/1.jpg", img);

    return 0;
}

3、opencv-Fast角点检测算法python版代码

# -*- coding: utf-8 -*-
"""
Created on Mon Mar 13 21:06:59 2017

@author: lql0716
"""

import cv2

img = cv2.imread('D:/photo/01.jpg')
gray = cv2.cvtColor(img, cv2.COLOR_BGR2GRAY)
fast = cv2.FeatureDetector_create('FAST')
kp = fast.detect(gray, None)
img2 = cv2.drawKeypoints(img, kp, (0, 0, 255))

cv2.namedWindow('img', cv2.WINDOW_NORMAL)
cv2.imshow('img', img2)
cv2.imwrite('D:/photo/01_1.jpg', img2)
cv2.waitKey(0)

SIFT算法

1、SIFT综述

尺度不变特征转换(Scale-invariant feature transform或SIFT)是一种电脑视觉的算法用来侦测与描述影像中的局部性特征，它在空间尺度中寻找极值点，并提取出其位置、尺度、旋转不变量，此算法由 David Lowe在1999年所发表，2004年完善总结。

其应用范围包含物体辨识、机器人地图感知与导航、影像缝合、3D模型建立、手势辨识、影像追踪和动作比对。

此算法有其专利，专利拥有者为英属哥伦比亚大学。

局部影像特征的描述与侦测可以帮助辨识物体，SIFT 特征是基于物体上的一些局部外观的兴趣点而与影像的大小和旋转无关。对于光线、噪声、些微视角改变的容忍度也相当高。基于这些特性，它们是高度显著而且相对容易撷取，在母数庞大的特征数据库中，很容易辨识物体而且鲜有误认。使用 SIFT特征描述对于部分物体遮蔽的侦测率也相当高，甚至只需要3个以上的SIFT物体特征就足以计算出位置与方位。在现今的电脑硬件速度下和小型的特征数据库条件下，辨识速度可接近即时运算。SIFT特征的信息量大，适合在海量数据库中快速准确匹配。

SIFT算法的特点有：

1. SIFT特征是图像的局部特征，其对旋转、尺度缩放、亮度变化保持不变性，对视角变化、仿射变换、噪声也保持一定程度的稳定性；

2. 独特性（Distinctiveness）好，信息量丰富，适用于在海量特征数据库中进行快速、准确的匹配；

3. 多量性，即使少数的几个物体也可以产生大量的SIFT特征向量；

4. 高速性，经优化的SIFT匹配算法甚至可以达到实时的要求；

5. 可扩展性，可以很方便的与其他形式的特征向量进行联合。

SIFT算法可以解决的问题：

目标的自身状态、场景所处的环境和成像器材的成像特性等因素影响图像配准/目标识别跟踪的性能。而SIFT算法在一定程度上可解决：

1. 目标的旋转、缩放、平移（RST）

2. 图像仿射/投影变换（视点viewpoint）

3. 光照影响（illumination）

4. 目标遮挡（occlusion）

5. 杂物场景（clutter）

6. 噪声

SIFT算法的实质是在不同的尺度空间上查找关键点(特征点)，并计算出关键点的方向。SIFT所查找到的关键点是一些十分突出，不会因光照，仿射变换和噪音等因素而变化的点，如角点、边缘点、暗区的亮点及亮区的暗点等。

Lowe将SIFT算法分解为如下四步：

1. 尺度空间极值检测：搜索所有尺度上的图像位置。通过高斯微分函数来识别潜在的对于尺度和旋转不变的兴趣点。

2. 关键点定位：在每个候选的位置上，通过一个拟合精细的模型来确定位置和尺度。关键点的选择依据于它们的稳定程度。

3. 方向确定：基于图像局部的梯度方向，分配给每个关键点位置一个或多个方向。所有后面的对图像数据的操作都相对于关键点的方向、尺度和位置进行变换，从而提供对于这些变换的不变性。

4. 关键点描述：在每个关键点周围的邻域内，在选定的尺度上测量图像局部的梯度。这些梯度被变换成一种表示，这种表示允许比较大的局部形状的变形和光照变化。

本文沿着Lowe的步骤，参考Rob Hess及Andrea Vedaldi源码，详解SIFT算法的实现过程。

2. 尺度空间

在一定的范围内，无论物体是大还是小，人眼都可以分辨出来。然而计算机要有相同的能力却不是那么的容易，在未知的场景中，计算机视觉并不能提供物体的尺度大小，其中的一种方法是把物体不同尺度下的图像都提供给机器，让机器能够对物体在不同的尺度下有一个统一的认知。在建立统一认知的过程中，要考虑的就是在图像在不同的尺度下都存在的特征点。

2.1 多分辨率图像金字塔

在早期图像的多尺度通常使用图像金字塔表示形式。图像金字塔是同一图像在不同的分辨率下得到的一组结果，其生成过程一般包括两个步骤：

对原始图像进行平滑
对处理后的图像进行降采样（通常是水平、垂直方向的1/2）
降采样后得到一系列不断尺寸缩小的图像。显然，一个传统的金字塔中，每一层的图像是其上一层图像长、高的各一半。多分辨率的图像金字塔虽然生成简单，但其本质是降采样，图像的局部特征则难以保持，也就是无法保持特征的尺度不变性。

2.2 高斯尺度空间

我们还可以通过图像的模糊程度来模拟人在距离物体由远到近时物体在视网膜上成像过程，距离物体越近其尺寸越大图像也越模糊，这就是高斯尺度空间，使用不同的参数模糊图像（分辨率不变），是尺度空间的另一种表现形式。
我们知道图像和高斯函数进行卷积运算能够对图像进行模糊，使用不同的“高斯核”可得到不同模糊程度的图像。一副图像其高斯尺度空间可由其和不同的高斯卷积得到：

其中，𝐿(𝑥,𝑦,𝜎)是图像的高斯尺度空间。
从上式可以知道，将相邻的两个高斯空间的图像相减就得到了DoG的响应图像。为了得到DoG图像，先要构建高斯尺度空间，而高斯的尺度空间可以在图像金字塔降采样的基础上加上高斯滤波得到，也就是对图像金字塔的每层图像使用不同的参数𝜎进行高斯模糊，使每层金字塔有多张高斯模糊过的图像。降采样时，金字塔上边一组图像的第一张是由其下面一组图像倒数第三张降采样得到。
易知，高斯金字塔有多组，每组又有多层。一组中的多个层之间的尺度是不一样的（也就是使用的高斯参数𝜎是不同的），相邻两层之间的尺度相差一个比例因子𝑘。如果每组有𝑆层，则𝑘=21𝑆。上一组图像的最底层图像是由下一组中尺度为2𝜎的图像进行因子为2的降采样得到的（高斯金字塔先从底层建立）。高斯金字塔构建完成后，将相邻的高斯金字塔相减就得到了DoG金字塔。
高斯金字塔的组数一般是

3. DoG空间极值检测

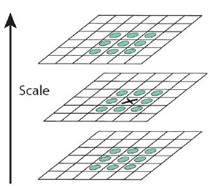
为了寻找尺度空间的极值点，每个像素点要和其图像域（同一尺度空间）和尺度域（相邻的尺度空间）的所有相邻点进行比较，当其大于（或者小于）所有相邻点时，改点就是极值点。如图所示，中间的检测点要和其所在图像的3×3

邻域8个像素点，以及其相邻的上下两层的3×3领域18个像素点，共26个像素点进行比较。
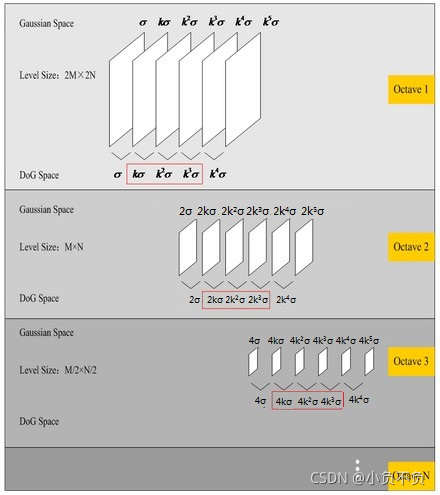
从上面的描述中可以知道，每组图像的第一层和最后一层是无法进行比较取得极值的。为了满足尺度变换的连续性，在每一组图像的顶层继续使用高斯模糊生成3幅图像，高斯金字塔每组有𝑆+3层图像，DoG金字塔的每组有𝑆+2组图像。

3.1 尺度变化的连续性

设𝑆=3

，也就是每组有3层，则𝑘=21𝑆=213，也就是有高斯金字塔每组有(𝑆−1)3层图像，𝐷𝑜𝐺金字塔每组有(S-2)2层图像。在DoG金字塔的第一组有两层尺度分别是𝜎,𝑘𝜎，第二组有两层的尺度分别是2𝜎,2𝑘𝜎，由于只有两项是无法比较取得极值的（只有左右两边都有值才能有极值）。由于无法比较取得极值，那么我们就需要继续对每组的图像进行高斯模糊，使得尺度形成𝜎,𝑘𝜎,𝑘2𝜎,𝑘3𝜎,𝑘4𝜎，这样就可以选择中间的三项𝑘𝜎,𝑘2𝜎,𝑘3𝜎。对应的下一组由上一组降采样得到的三项是2𝑘𝜎,2𝑘2𝜎,2𝑘3𝜎，其首项2𝑘𝜎=2⋅213𝜎=243𝜎，刚好与上一组的最后一项𝑘3𝜎=233𝜎的尺度连续起来。

4. 删除不好的极值点（特征点）

通过比较检测得到的DoG的局部极值点实在离散的空间搜索得到的，由于离散空间是对连续空间采样得到的结果，因此在离散空间找到的极值点不一定是真正意义上的极值点，因此要设法将不满足条件的点剔除掉。可以通过尺度空间DoG函数进行曲线拟合寻找极值点，这一步的本质是去掉DoG局部曲率非常不对称的点。
要剔除掉的不符合要求的点主要有两种：

低对比度的特征点
不稳定的边缘响应点

6. 生成特征描述

通过以上的步骤已经找到了SIFT特征点位置、尺度和方向信息，下面就需要使用一组向量来描述关键点也就是生成特征点描述子，这个描述符不只包含特征点，也含有特征点周围对其有贡献的像素点。描述子应具有较高的独立性，以保证匹配率。
特征描述符的生成大致有三个步骤：

校正旋转主方向，确保旋转不变性。
生成描述子，最终形成一个128维的特征向量
归一化处理，将特征向量长度进行归一化处理，进一步去除光照的影响。

为了保证特征矢量的旋转不变性，要以特征点为中心，在附近邻域内将坐标轴旋转𝜃

（特征点的主方向）角度，即将坐标轴旋转为特征点的主方向。旋转后邻域内像素的新坐标为：

7. 总结

SIFT特征以其对旋转、尺度缩放、亮度等保持不变性，是一种非常稳定的局部特征，在图像处理和计算机视觉领域有着很重要的作用，其本身也是非常复杂的，下面对其计算过程做一个粗略总结。

DoG尺度空间的极值检测。首先是构造DoG尺度空间，在SIFT中使用不同参数的高斯模糊来表示不同的尺度空间。而构造尺度空间是为了检测在不同尺度下都存在的特征点，特征点的检测比较常用的方法是Δ2𝐺

（高斯拉普拉斯LoG），但是LoG的运算量是比较大的，Marr和Hidreth曾指出，可以使用DoG（差分高斯）来近似计算LoG，所以在DoG的尺度空间下检测极值点。
删除不稳定的极值点。主要删除两类：低对比度的极值点以及不稳定的边缘响应点。
** 确定特征点的主方向**。以特征点的为中心、以3×1.5𝜎
为半径的领域内计算各个像素点的梯度的幅角和幅值，然后使用直方图对梯度的幅角进行统计。直方图的横轴是梯度的方向，纵轴为梯度方向对应梯度幅值的累加值，直方图中最高峰所对应的方向即为特征点的方向。
生成特征点的描述子。首先将坐标轴旋转为特征点的方向，以特征点为中心的16×16

的窗口的像素的梯度幅值和方向，将窗口内的像素分成16块，每块是其像素内8个方向的直方图统计，共可形成128维的特征向量。

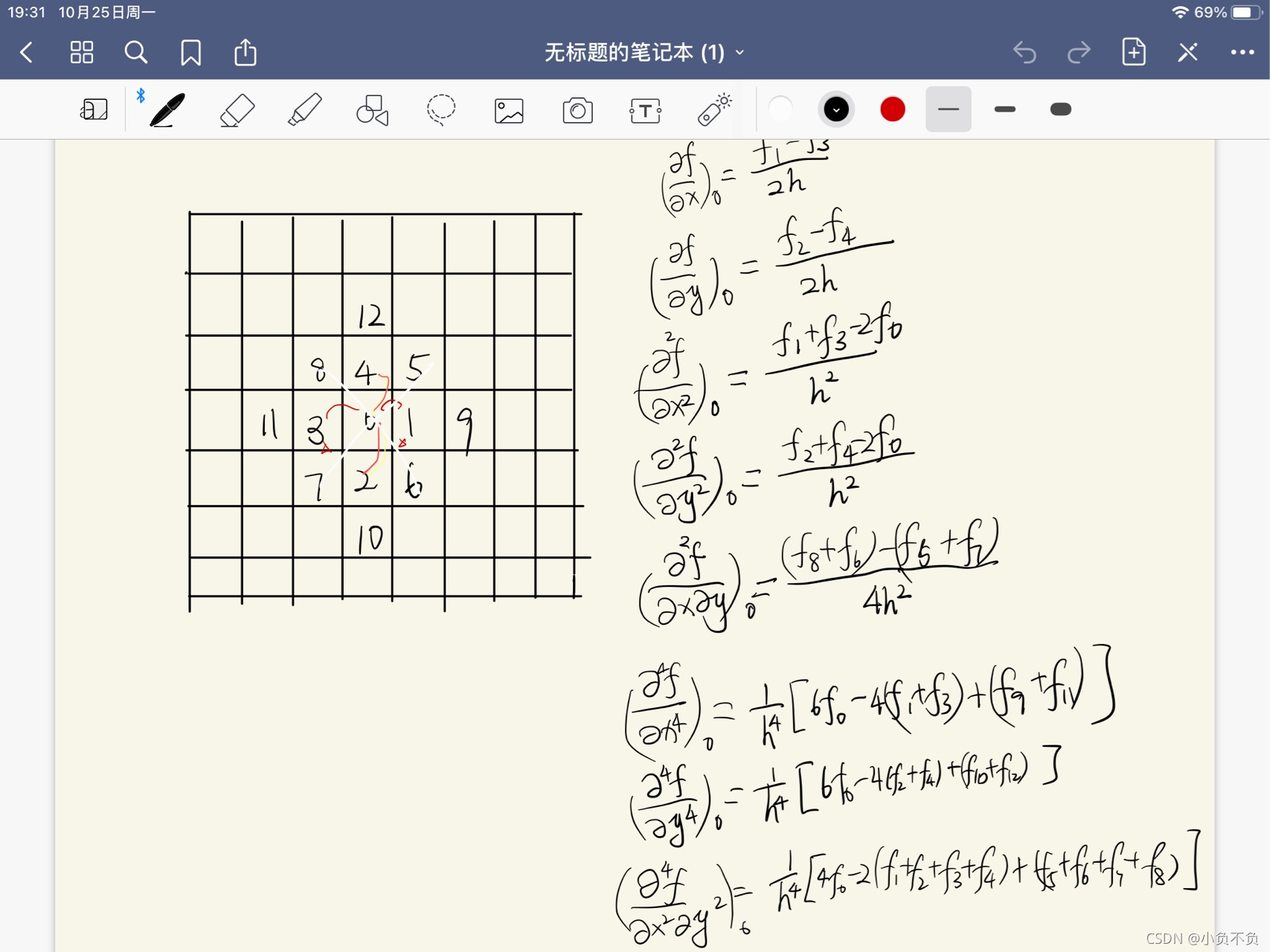
原文链接：https://blog.csdn.net/zddblog/article/details/7521424

SIFT特征详解 - Brook_icv - 博客园

SIFT python代码实现

import cv2
import numpy as np
from matplotlib import pyplot as plt
 
img = cv2.imread('test30.jpg')
img1 = img.copy()
gray = cv2.cvtColor(img, cv2.COLOR_BGR2GRAY)
 
sift = cv2.xfeatures2d.SIFT_create()
kp = sift.detect(gray, None)
 
cv2.drawKeypoints(gray, kp, img)
cv2.drawKeypoints(gray, kp, img1, flags=cv2.DRAW_MATCHES_FLAGS_DRAW_RICH_KEYPOINTS)
 
plt.subplot(121), plt.imshow(img),
plt.title('Dstination'), plt.axis('off')
plt.subplot(122), plt.imshow(img1),
plt.title('Dstination'), plt.axis('off')
plt.show()

SUFT算法

SURF（Speeded Up Robust Features）是对SIFT的一种改进，主要特点是快速。SURF与SIFT主要有以下几点不同处理：

1、 SIFT在构造DOG金字塔以及求DOG局部空间极值比较耗时，SURF的改进是使用Hessian矩阵变换图像，极值的检测只需计算Hessian矩阵行列式，作为进一步优化，使用一个简单的方程可以求出Hessian行列式近似值，使用盒状模糊滤波（box blur）求高斯模糊近似值。

2、 SURF不使用降采样，通过保持图像大小不变，但改变盒状滤波器的大小来构建尺度金字塔。

3、在计算关键点主方向以及关键点周边像素方向的方法上，SURF不使用直方图统计，而是使用哈尔(haar)小波转换。SIFT的KPD达到128维，导致KPD的比较耗时，SURF使用哈尔(haar)小波转换得到的方向，让SURF的KPD降到64维，减少了一半，提高了匹配速度

如果说SIFT算法中使用DOG对LOG进行了简化，提高了搜索特征点的速度，那么SURF算法则是对DoH的简化与近似。虽然SIFT算法已经被认为是最有效的，也是最常用的特征点提取的算法，但如果不借助于硬件的加速和专用图像处理器的配合，SIFT算法以现有的计算机仍然很难达到实时的程度。对于需要实时运算的场合，如基于特征点匹配的实时目标跟踪系统，每秒要处理8-24帧的图像，需要在毫秒级内完成特征点的搜索、特征矢量生成、特征矢量匹配、目标锁定等工作，这样SIFT算法就很难适应这种需求了。SURF借鉴了SIFT中简化近似的思想，把DoH中的高斯二阶微分模板进行了简化，使得模板对图像的滤波只需要进行几个简单的加减法运算，并且，这种运算与滤波器的尺度无关。实验证明，SURF算法较SIFT在运算速度上要快3倍左右。

1. 积分图像

SURF算法中要用到积分图像的概念。借助积分图像，图像与高斯二阶微分模板的滤波转化为对积分图像的加减运算。

积分图像中任意一点(i,j)的值 ii(i,j) ，为原图像左上角到点(i,j)相应的对角线区域灰度值的总和，即

$ii(i,j)=\sum_{r\leqslant i,c \leqslant j}^{ } p(r,c)$

式中，p(r,c)表示图像中点(r,c)的灰度值， ii(i,j) 可以用下面两式迭代计算得到

式中，S(i,j)表示一列的积分，且S(i,−1)=0 , ii(-1,j) =0。求积分图像，只需要对原图像所有像素进行一遍扫描。

OpenCV中提供了用于计算积分图像的接口

*src :输入图像，大小为M*N
* sum: 输出的积分图像，大小为（M+1）*（N+1）
* sdepth：用于指定sum的类型，-1表示与src类型一致
*/
void integral(InputArray src, OutputArray sum, int sdepth = -1);

值得注意的是OpenCV里的积分图大小比原图像多一行一列，那是因为OpenCV中积分图的计算公式为：
$ii(i,j)=\sum_{r< i,c <j}^{ } p(r,c)$
一旦积分图计算好了，计算图像内任何矩形区域的像素值的和只需要三个加法，如下图所示：

2. DoH近似

surf构造的金字塔图像与sift有很大不同，Sift采用的是DOG图像，而surf采用的是Hessian矩阵行列式近似值图像。

Hessian矩阵是Surf算法的核心，构建Hessian矩阵的目的是为了生成图像稳定的边缘点（突变点），为下文的特征提取做好基础。每一个像素点都可以求出一个Hessian矩阵：

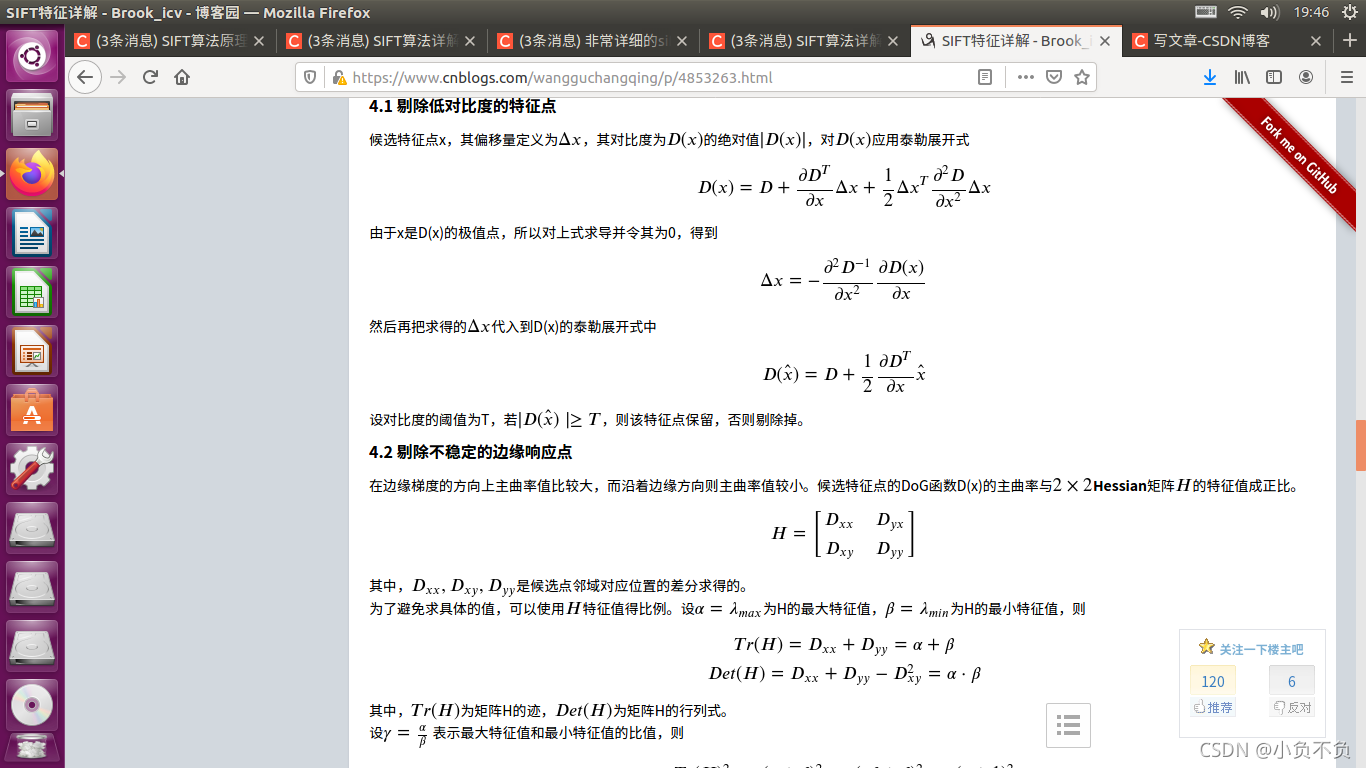
当Hessian矩阵的判别式取得局部极大值时，判定当前点是比周围邻域内其他点更亮或更暗的点，由此来定位关键点的位置，Hessian矩阵的判别式为：

，

在SURF算法中，图像像素l(x，y)即为函数值f(x，y)。但是由于我们的特征点需要具备尺度无关性，所以在进行Hessian矩阵构造前，需要对其进行高斯滤波，选用二阶标准高斯函数作为滤波器。通过特定核间的卷积计算二阶偏导数，这样便能计算出H矩阵的三个矩阵元素L_xx, L_xy, L_yy从而计算出H矩阵，在点x处，尺度为σ的Hessian矩阵H(x,σ)定义如下：

式中， $L_{xx}(x,\sigma )$ 是高斯二阶微分在在像素点（x,y）处与图像函数I(x,y)的卷积。

下面显示的是上面三种高斯微分算子的图形。

但是利用Hessian行列式进行图像斑点检测时，有一个缺点。由于二阶高斯微分被离散化和裁剪的原因，导致了图像在旋转奇数倍的 $\pi /4$ 时，即转换到模板的对角线方向时，特征点检测的重复性降低（也就是说，原来特征点的地方，可能检测不到特征点了）。而在 $\pi /2$ 时，特征点检测的重现率真最高。但这一小小的不足不影响我们使用Hessian矩阵进行特征点的检测。

盒式滤波器

由于高斯核是服从正态分布的，从中心点往外，系数越来越低，为了提高运算速度，Surf使用了盒式滤波器来近似替代高斯滤波器，提高运算速度。 盒式滤波器（Boxfilter）对图像的滤波转化成计算图像上不同区域间像素和的加减运算问题，只需要简单几次查找积分图就可以完成。每个像素的Hessian矩阵行列式的近似值：，在Dxy上乘了一个加权系数0.9，目的是为了平衡因使用盒式滤波器近似所带来的误差。

高斯函数的高阶微分与离散的图像函数I(x,y)做卷积运算时相当于使用高斯滤波模板对图像做滤波处理。

在实际运用中，高斯二阶微分进行离散化和裁剪处理得到盒子滤波器近似代替高斯滤波板进行卷积计算，我们需要对高斯二阶微分模板进行简化，使得简化后的模板只是由几个矩形区域组成，矩形区域内填充同一值，如下图所示，在简化模板中白色区域的值为正数，黑色区域的值为负数，灰度区域的值为0。

对于σ=1.2的高斯二阶微分滤波器，我们设定模板的尺寸为9×9的大小，并用它作为最小尺度空间值对图像进行滤波和斑点检测。我们使用Dxx、Dxy和Dyy表示模板与图像进行卷积的结果。这样，便可以将Hessian矩阵的行列式作如下的简化：

滤波器响应的相关权重w是为了平衡Hessian行列式的表示式。这是为了保持高斯核与近似高斯核的一致性。

其中 $|X|_{F}$ 为Frobenius范数。理论上来说对于不同的σ的值和对应尺寸的模板尺寸，w值是不同的，但为了简化起见，可以认为它是同一个常数。

使用近似的Hessian矩阵行列式来表示图像中某一点x处的斑点响应值，遍历图像中所有的像元点，便形成了在某一尺度下关键点检测的响应图像。使用不同的模板尺寸，便形成了多尺度斑点响应的金字塔图像，利用这一金字塔图像，就可以进行斑点响应极值点的搜索，其过程完全与SIFT算法类同。

3. 尺度空间表示

通常想要获取不同尺度的斑点，必须建立图像的尺度空间金字塔。一般的方法是通过不同σ的高斯函数，对图像进行平滑滤波，然后重采样图像以获得更高一层的金字塔图像。SIFT特征检测算法中就是通过相邻两层图像金字塔相减得到DoG图像，然后再在DoG图像上进行斑点和边缘检测工作的。

由于采用了盒子滤波和积分图像，所以，我们并不需要像SIFT算法那样去直接建立图像金字塔，而是采用不断增大盒子滤波模板的尺寸的间接方法。通过不同尺寸盒子滤波模板与积分图像求取Hessian矩阵行列式的响应图像。然后在响应图像上采用3D非最大值抑制，求取各种不同尺度的斑点。

如前所述，我们使用9×9的模板对图像进行滤波，其结果作为最初始的尺度空间层（此时，尺度值为s=1.2，近似σ=1.2的高斯微分），后续的层将通过逐步放大滤波模板尺寸，以及放大后的模板不断与图像进行滤波得到。由于采用盒子滤波和积分图像，滤波过程并不随着滤波模板尺寸的增加而使运算工作量增加。

与SIFT算法类似，我们需要将尺度空间划分为若干组（Octaves）。一个组代表了逐步放大的滤波模板对同一输入图像进行滤波的一系列响应图。每个组又由若干固定的层组成。由于积分图像离散化的原因，两个层之间的最小尺度变化量是由高斯二阶微分滤波器在微分方向上对正负斑点响应长度 $l_{0}$ 决定的，它是盒子滤波器模板尺寸的1/3。对于9×9的模板，它的 $l_{0}$ =3。下一层的响应长度至少应该在 $l_{0}$ 的基础上增加2个像素，以保证一边一个像素，即 $l_{0}$ =5。这样模板的尺寸就为15×15。以此类推，我们可以得到一个尺寸增大模板序列，它们的尺寸分别为：9×9，15×15，21×21，27×279×9，15×15，21×21，27×27，黑色、白色区域的长度增加偶数个像素，以保证一个中心像素的存在。

采用类似的方法来处理其他几组的模板序列。其方法是将滤波器尺寸增加量翻倍（6，12，24，38）。这样，可以得到第二组的滤波器尺寸，它们分别为15，27，39，51。第三组的滤波器尺寸为27，51，75，99。如果原始图像的尺寸仍然大于对应的滤波器尺寸，尺度空间的分析还可以进行第四组，其对应的模板尺寸分别为51，99，147和195。下图显示了第一组至第三组的滤波器尺寸变化。

在通常尺度分析情况下，随着尺度的增大，被检测到的斑点数量迅速衰减。所以一般进行3-4组就可以了，与此同时，为了减少运算量，提高计算的速度，可以考虑在滤波时，将采样间隔设为2。

对于尺寸为L的模板，当用它与积分图运算来近似二维高斯核的滤波时，对应的二维高斯核的参数σ=1.2×(L/9)，这一点至关重要，尤其是在后面计算描述子时，用于计算邻域的半径时。

Hessian行列式图像的产生过程

在SURF算法的尺度空间中，每一组中任意一层包括 $D_{xx},D_{yy},D_{xy}$ 三种盒子滤波器。对一幅输入图像进行滤波后通过Hessian行列式计算公式可以得到对于尺度坐标下的Hessian行列式的值，所有Hessian行列式值构成一幅Hessian行列式图像。

4. 兴趣点的定位

为了在图像及不同尺寸中定位兴趣点，我们用了3×3×3邻域非最大值抑制。具体的步骤基本与SIFT一致，而且Hessian矩阵行列式的最大值在尺度和图像空间被插值。

总体来说，如果理解了SIFT算法，再来看SURF算法会发现思路非常简单。尤其是局部最大值查找方面，基本一致。关键还是一个用积分图来简化卷积的思路，以及怎么用不同的模板来近似原来尺度空间中的高斯滤波器。

5. SURF特征点方向分配

为了保证特征矢量具有旋转不变性，与SIFT特征一样，需要对每个特征点分配一个主方向。为些，我们需要以特征点为中心，以6*s（s=1.2∗L/9为特征点的尺度）为半径的圆形区域，对图像进行Haar小波响应运算。这样做实际就是对图像进行梯度运算只不过是我们需要利用积分图像，提高计算图像梯度的效率。在SIFT特征描述子中我们在求取特征点主方向时，以是特征点为中心，在以4.5σ为半径的邻域内计算梯度方向直方图。事实上，两种方法在求取特征点主方向时，考虑到Haar小波的模板带宽，实际计算梯度的图像区域是相同的。用于计算梯度的Harr小波的尺度为4s。

其中左侧模板计算X方向的响应，右侧模板计算y方向的响应，黑色表示-1，白色表示+1。用其对圆形领域进行处理后，就得到了该领域内每个点对应的x,y方向的响应，然后用以兴趣点为中心的高斯函数（ $\sigma =2s$ ）对这些响应进行加权。

为了求取主方向值，需要设计一个以特征点为中心，张角为60度的扇形滑动窗口，统计这个扇形区域内的haar小波特征总和。以步长为0.2弧度左右，旋转这个滑动窗口，再统计小波特征总和。小波特征总和最大的方向为主方向。特征总和的求法是对图像Harr小波响应值dx、dy进行累加，得到一个矢量 $(m_{w},\theta _{w})$ ：

主方向为最大Harr响应累加值所对应的方向，也就是最长矢量所对应的方向，即

可以依照SIFT求方向时策略，当存在另一个相当于主峰值80%能量的峰值时，则将这个方向认为是该特征点的辅方向。一个特征点可能会被指定具有多个方向（一个主方向，一个以上辅方向），这可以增强匹配的鲁棒性。和SIFT的描述子类似，如果在 $m_{w}$ 中出现另一个大于主峰能量 $max[m_{w}]$ 的80%时的次峰，可以将该特征点复制成两个特征点。一个主的方向为最大响应能量所对应的方向，另一个主方向为次大响应能量所对应的方向。

5.1 特征点特征矢量生成

在SIFT中关键点描述是选取了关键点周围16*16的领域，又将其划分为4*4的区域，每个区域统计8个方向梯度，最后得到4*4*8=128维度的描述向量。

SURF中，我们在关键点周围选取一个正方形框，方向为关键点的主方向，边长为20S。将其划分为16个区域（边长为5S），每个区域统计25个像素的水平方向和垂直方向的Haar小波特性（均相对于正方形框的主方向确定的）

生成特征点描述子，需要计算图像的Haar小波响应。在一个矩形区域来计算Haar小波响应。以特征点为中心，沿上一节讨论得到的主方向，沿主方向将20s×20s的图像划分为4×4个子块，每个子块利用尺寸2s的Harr模板进行响应值计算，然后对响应值进行统计∑dx、∑|dx|、∑dy、∑|dy|形成特征矢量。如下图2所示。图中，以特征点为中心，以20s为边长的矩形窗口为特征描述子计算使用的窗口，特征点到矩形边框的线段表示特征点的主方向。

将20s的窗口划分成4×4子窗口，每个子窗口有5s×5s个像素。使用尺寸为2s的Harr小波对子窗口图像进行其响应值计算，共进行25次采样，分别得到沿主方向的dy和垂直于主方向的dx。然后，以特征点为中心，对dy和dx进行高斯加权计算，高斯核的参数为σ=3.3s(即20s/6)。最后分别对每个子块的响应值进行统计，得到每个子块的矢量：

由于共有4×4个子块，因此，特征描述子共由4×4×4=64维特征矢量组成。SURF描述子不仅具有尺度和旋转不变性，而且对光照的变化也具有不变性。使小波响应本身就具有亮度不变性，而对比度的不变性则是通过将特征矢量进行归一化来实现。图3 给出了三种不同图像模式的子块得到的不同结果。对于实际图像的描述子，我们可以认为它们是由这三种不同模式图像的描述子组合而成的。

为了充分利用积分图像进行Haar小波的响应计算，我们并不直接旋转Haar小波模板求得其响应值，而是在积图像上先使用水平和垂直的Haar模板求得响应值dy和dx，然后根据主方向旋转dx和dy与主方向操持一致，如下图4所示。为了求得旋转后Haar小波响应值，首先要得到旋转前图像的位置。旋转前后图偈的位置关系，可以通过点的旋转公式得到：

在得到点(j,i)在旋转前对应积分图像的位置(x,y)后，利用积分图像与水平、垂直Harr小波，求得水平与垂直两个方向的响应值dx和dy。对dx和dy进行高斯加权处理，并根据主方向的角度，对dx和dy进行旋转变换，从而，得到旋转后的dx’和dy’。其计算公式如下：

5.2 特征描述子的维数

一般而言，特征矢量的长度越长，特征矢量所承载的信息量就越大，特征描述子的独特性就越好，但匹配时所付出的时间代价就越大。对于SURF描述子，可以将它扩展到用128维矢量来表示。具体方法是在求∑dx、∑|dx|时区分dy<0和dy≥0情况。同时，在求取∑dy、∑|dy|时区分dx<0和dx≥0情况。这样，每个子块就产生了8个梯度统计值，从而使描述子特征矢量的长度增加到8×4×4=128维。

为了实现快速匹配，SURF在特征矢量中增加了一个新的变量，即特征点的拉普拉斯响应正负号。在特征点检测时，将Hessian矩阵的迹的正负号记录下来，作为特征矢量中的一个变量。这样做并不增加运算量，因为特征点检测进已经对Hessian矩阵的迹进行了计算。在特征匹配时，这个变量可以有效地节省搜索的时间，因为只有两个具有相同正负号的特征点才有可能匹配，对于正负号不同的特征点就不进行相似性计算。

简单地说，我们可以根据特征点的响应值符号，将特征点分成两组，一组是具有拉普拉斯正响应的特征点，一组是具有拉普拉斯负响应的特征点，匹配时，只有符号相同组中的特征点才能进行相互匹配。显然，这样可以节省特征点匹配的时间。如下图5所示。

实际上有文献指出，SURF比SIFT工作更出色。他们认为主要是因为SURF在求取描述子特征矢量时，是对一个子块的梯度信息进行求和，而SIFT则是依靠单个像素梯度的方向。

SURF算法与SIFT算法总结对比

（1）在生成尺度空间方面，SIFT算法利用的是差分高斯金字塔与不同层级的空间图像相互卷积生成。SURF算法采用的是不同尺度的box filters与原图像卷积

（2）在特征点检验时，SIFT算子是先对图像进行非极大值抑制，再去除对比度较低的点。然后通过Hessian矩阵去除边缘的点。

而SURF算法是先通过Hessian矩阵来检测候选特征点，然后再对非极大值的点进行抑制

（3）在特征向量的方向确定上，SIFT算法是在正方形区域内统计梯度的幅值的直方图，找到最大梯度幅值所对应的方向。SIFT算子确定的特征点可以有一个或一个以上方向，其中包括一个主方向与多个辅方向。

SURF算法则是在圆形邻域内，检测各个扇形范围内水平、垂直方向上的Haar小波响应，找到模值最大的扇形指向，且该算法的方向只有一个。

（4）SIFT算法生成描述子时，是将16*16的采样点划分为4*4的区域，从而计算每个分区种子点的幅值并确定其方向，共计4*4*8=128维。

SURF算法在生成特征描述子时将20s*20s的正方形分割成4*4的小方格，每个子区域25个采样点，计算小波haar响应，一共4*4*4=64维。

综上，SURF算法在各个步骤上都简化了一些繁琐的工作，仅仅计算了特征点的一个主方向，生成的特征描述子也与前者相比降低了维数。

from：【CV学习5】SURF算法详解 - 苟富贵 - 博客园

——————————————————————————————————————————

SUFT源码解析

这份源码来自OpenCV nonfree模块。

1 主干函数 fastHessianDetector

特征点定位的主干函数为fastHessianDetector，该函数接受一个积分图像，以及尺寸相关的参数，组数与每组的层数，检测到的特征点保存在vector<KeyPoint>类型的结构中。

static void fastHessianDetector(const Mat& sum, const Mat& msum, vector<KeyPoint>& keypoints,
    int nOctaves, int nOctaveLayers, float hessianThreshold)
{
    /*first Octave图像采样的步长，第二组的时候加倍，以此内推
    增加这个值，将会加快特征点检测的速度，但是会让特征点的提取变得不稳定*/
    const int SAMPLE_STEP0 = 1;
 
    int nTotalLayers = (nOctaveLayers + 2)*nOctaves; // 尺度空间的总图像数
    int nMiddleLayers = nOctaveLayers*nOctaves; // 用于检测特征点的层的 总数，也就是中间层的总数
 
    vector<Mat> dets(nTotalLayers); // 每一层图像 对应的 Hessian行列式的值
    vector<Mat> traces(nTotalLayers); // 每一层图像 对应的 Hessian矩阵的迹的值
    vector<int> sizes(nTotalLayers); // 每一层用的 Harr模板的大小
    vector<int> sampleSteps(nTotalLayers); // 每一层用的采样步长 
    vector<int> middleIndices(nMiddleLayers); // 中间层的索引值
 
    keypoints.clear();
 
    // 为上面的对象分配空间，并赋予合适的值
    int index = 0, middleIndex = 0, step = SAMPLE_STEP0;
 
    for (int octave = 0; octave < nOctaves; octave++)
    {
        for (int layer = 0; layer < nOctaveLayers + 2; layer++)
        {
            /*这里sum.rows - 1是因为 sum是积分图，它的大小是原图像大小加1*/
            dets[index].create((sum.rows - 1) / step, (sum.cols - 1) / step, CV_32F); // 这里面有除以遍历图像用的步长
            traces[index].create((sum.rows - 1) / step, (sum.cols - 1) / step, CV_32F);
            sizes[index] = (SURF_HAAR_SIZE0 + SURF_HAAR_SIZE_INC*layer) << octave;
            sampleSteps[index] = step;
 
            if (0 < layer && layer <= nOctaveLayers)
                middleIndices[middleIndex++] = index;
            index++;
        }
        step *= 2;
    }
    // Calculate hessian determinant and trace samples in each layer
    for (int i = 0; i < nTotalLayers; i++)
    {
        calcLayerDetAndTrace(sum, sizes[i], sampleSteps[i], dets[i], traces[i]);
    }
 
    // Find maxima in the determinant of the hessian
    for (int i = 0; i < nMiddleLayers; i++)
    {
        int layer = middleIndices[i];
        int octave = i / nOctaveLayers;
        findMaximaInLayer(sum, msum, dets, traces, sizes, keypoints, octave, layer, hessianThreshold, sampleSteps[layer]);
    }
 
    std::sort(keypoints.begin(), keypoints.end(), KeypointGreater());
}

2 计算Hessian矩阵的行列式与迹calcLayerDetAndTrace

这个函数首先定义了尺寸为9的第一层图像的三个模板。模板分别为一个3×5、3×5、4×5的二维数组表示，数组的每一行表示一个黑白块的位置参数。函数里只初始化了第一层图像的模板参数，后面其他组其他层的Harr模板参数都是用resizeHaarPattern 这个函数来计算的。这个函数返回的是一个SurfHF的结构体，这个结构体由两个点及一个权重构成。

struct SurfHF
{
    int p0, p1, p2, p3;
    float w;
 
    SurfHF() : p0(0), p1(0), p2(0), p3(0), w(0) {}
};

static void
resizeHaarPattern(const int src[][5], SurfHF* dst, int n, int oldSize, int newSize, int widthStep)
{
    float ratio = (float)newSize / oldSize;
    for (int k = 0; k < n; k++)
    {
        int dx1 = cvRound(ratio*src[k][0]);
        int dy1 = cvRound(ratio*src[k][1]);
        int dx2 = cvRound(ratio*src[k][2]);
        int dy2 = cvRound(ratio*src[k][3]);
        /*巧妙的坐标转换*/
        dst[k].p0 = dy1*widthStep + dx1; // 转换为一个相对距离，距离模板左上角点的  在积分图中的距离 !!important!!
        dst[k].p1 = dy2*widthStep + dx1; 
        dst[k].p2 = dy1*widthStep + dx2;
        dst[k].p3 = dy2*widthStep + dx2;
        dst[k].w = src[k][4] / ((float)(dx2 - dx1)*(dy2 - dy1));// 原来的+1,+2用 覆盖的所有像素点平均。
    }
}

在用积分图计算近似卷积时，用的是calcHaarPattern函数。这个函数比较简单，只用知道左上与右下角坐标即可。

inline float calcHaarPattern(const int* origin, const SurfHF* f, int n)
{
    /*orgin即为积分图，n为模板中 黑白 块的个数 */
    double d = 0;
    for (int k = 0; k < n; k++)
        d += (origin[f[k].p0] + origin[f[k].p3] - origin[f[k].p1] - origin[f[k].p2])*f[k].w;
    return (float)d;
}

最终我们可以看到了整个calcLayerDetAndTrack的代码

static void calcLayerDetAndTrace(const Mat& sum, int size, int sampleStep,
    Mat& det, Mat& trace)
{
    const int NX = 3, NY = 3, NXY = 4;
    const int dx_s[NX][5] = { { 0, 2, 3, 7, 1 }, { 3, 2, 6, 7, -2 }, { 6, 2, 9, 7, 1 } };
    const int dy_s[NY][5] = { { 2, 0, 7, 3, 1 }, { 2, 3, 7, 6, -2 }, { 2, 6, 7, 9, 1 } };
    const int dxy_s[NXY][5] = { { 1, 1, 4, 4, 1 }, { 5, 1, 8, 4, -1 }, { 1, 5, 4, 8, -1 }, { 5, 5, 8, 8, 1 } };
 
    SurfHF Dx[NX], Dy[NY], Dxy[NXY];
 
    if (size > sum.rows - 1 || size > sum.cols - 1)
        return;
    resizeHaarPattern(dx_s, Dx, NX, 9, size, sum.cols);
    resizeHaarPattern(dy_s, Dy, NY, 9, size, sum.cols);
    resizeHaarPattern(dxy_s, Dxy, NXY, 9, size, sum.cols);
 
    /* The integral image 'sum' is one pixel bigger than the source image */
    int samples_i = 1 + (sum.rows - 1 - size) / sampleStep; // 最大能遍历到的 行坐标，因为要减掉一个模板的尺寸
    int samples_j = 1 + (sum.cols - 1 - size) / sampleStep; // 最大能遍历到的 列坐标
 
    /* Ignore pixels where some of the kernel is outside the image */
    int margin = (size / 2) / sampleStep;
 
    for (int i = 0; i < samples_i; i++)
    {
        /*坐标为(i,j)的点是模板左上角的点，所以实际现在模板分析是的i+margin,j+margin点处的响应*/
        const int* sum_ptr = sum.ptr<int>(i*sampleStep);
        float* det_ptr = &det.at<float>(i + margin, margin); // 左边空隙为 margin
        float* trace_ptr = &trace.at<float>(i + margin, margin);
        for (int j = 0; j < samples_j; j++)
        {
            float dx = calcHaarPattern(sum_ptr, Dx, 3);
            float dy = calcHaarPattern(sum_ptr, Dy, 3);
            float dxy = calcHaarPattern(sum_ptr, Dxy, 4);
            sum_ptr += sampleStep;
            det_ptr[j] = dx*dy - 0.81f*dxy*dxy;
            trace_ptr[j] = dx + dy;
        }
    }
}

3 局部最大值搜索findMaximaInLayer

这里算法思路很简单，值得注意的是里面的一些坐标的转换很巧妙，里面比较重的函数就是interpolateKeypoint函数，通过插值计算最大值点。

/*
* Maxima location interpolation as described in "Invariant Features from
* Interest Point Groups" by Matthew Brown and David Lowe. This is performed by
* fitting a 3D quadratic to a set of neighbouring samples.
*
* The gradient vector and Hessian matrix at the initial keypoint location are
* approximated using central differences. The linear system Ax = b is then
* solved, where A is the Hessian, b is the negative gradient, and x is the
* offset of the interpolated maxima coordinates from the initial estimate.
* This is equivalent to an iteration of Netwon's optimisation algorithm.
*
* N9 contains the samples in the 3x3x3 neighbourhood of the maxima
* dx is the sampling step in x
* dy is the sampling step in y
* ds is the sampling step in size
* point contains the keypoint coordinates and scale to be modified
*
* Return value is 1 if interpolation was successful, 0 on failure.
*/
 
static int
interpolateKeypoint(float N9[3][9], int dx, int dy, int ds, KeyPoint& kpt)
{
    Vec3f b(-(N9[1][5] - N9[1][3]) / 2,  // Negative 1st deriv with respect to x
        -(N9[1][7] - N9[1][1]) / 2,  // Negative 1st deriv with respect to y
        -(N9[2][4] - N9[0][4]) / 2); // Negative 1st deriv with respect to s
 
    Matx33f A(
        N9[1][3] - 2 * N9[1][4] + N9[1][5],            // 2nd deriv x, x
        (N9[1][8] - N9[1][6] - N9[1][2] + N9[1][0]) / 4, // 2nd deriv x, y
        (N9[2][5] - N9[2][3] - N9[0][5] + N9[0][3]) / 4, // 2nd deriv x, s
        (N9[1][8] - N9[1][6] - N9[1][2] + N9[1][0]) / 4, // 2nd deriv x, y
        N9[1][1] - 2 * N9[1][4] + N9[1][7],            // 2nd deriv y, y
        (N9[2][7] - N9[2][1] - N9[0][7] + N9[0][1]) / 4, // 2nd deriv y, s
        (N9[2][5] - N9[2][3] - N9[0][5] + N9[0][3]) / 4, // 2nd deriv x, s
        (N9[2][7] - N9[2][1] - N9[0][7] + N9[0][1]) / 4, // 2nd deriv y, s
        N9[0][4] - 2 * N9[1][4] + N9[2][4]);           // 2nd deriv s, s
 
    Vec3f x = A.solve(b, DECOMP_LU);
 
    bool ok = (x[0] != 0 || x[1] != 0 || x[2] != 0) &&
        std::abs(x[0]) <= 1 && std::abs(x[1]) <= 1 && std::abs(x[2]) <= 1;
 
    if (ok)
    {
        kpt.pt.x += x[0] * dx;
        kpt.pt.y += x[1] * dy;
        kpt.size = (float)cvRound(kpt.size + x[2] * ds);
    }
    return ok;
}
 
static void findMaximaInLayer(const Mat& sum, const Mat& mask_sum,
    const vector<Mat>& dets, const vector<Mat>& traces,
    const vector<int>& sizes, vector<KeyPoint>& keypoints,
    int octave, int layer, float hessianThreshold, int sampleStep)
{
    // Wavelet Data
    const int NM = 1;
    const int dm[NM][5] = { { 0, 0, 9, 9, 1 } };
    SurfHF Dm;
 
    int size = sizes[layer];
 
    // 当前层图像的大小
    int layer_rows = (sum.rows - 1) / sampleStep;
    int layer_cols = (sum.cols - 1) / sampleStep;
 
    // 边界区域大小，考虑的下一层的模板大小
    int margin = (sizes[layer + 1] / 2) / sampleStep + 1;
 
    if (!mask_sum.empty())
        resizeHaarPattern(dm, &Dm, NM, 9, size, mask_sum.cols);
 
    int step = (int)(dets[layer].step / dets[layer].elemSize());
 
    for (int i = margin; i < layer_rows - margin; i++)
    {
        const float* det_ptr = dets[layer].ptr<float>(i);
        const float* trace_ptr = traces[layer].ptr<float>(i);
        for (int j = margin; j < layer_cols - margin; j++)
        {
            float val0 = det_ptr[j]; // 中心点的值
            if (val0 > hessianThreshold)
            {
                // 模板左上角的坐标
                int sum_i = sampleStep*(i - (size / 2) / sampleStep);
                int sum_j = sampleStep*(j - (size / 2) / sampleStep);
 
                /* The 3x3x3 neighbouring samples around the maxima.
                The maxima is included at N9[1][4] */
 
                const float *det1 = &dets[layer - 1].at<float>(i, j);
                const float *det2 = &dets[layer].at<float>(i, j);
                const float *det3 = &dets[layer + 1].at<float>(i, j);
                float N9[3][9] = { { det1[-step - 1], det1[-step], det1[-step + 1],
                    det1[-1], det1[0], det1[1],
                    det1[step - 1], det1[step], det1[step + 1] },
                    { det2[-step - 1], det2[-step], det2[-step + 1],
                    det2[-1], det2[0], det2[1],
                    det2[step - 1], det2[step], det2[step + 1] },
                    { det3[-step - 1], det3[-step], det3[-step + 1],
                    det3[-1], det3[0], det3[1],
                    det3[step - 1], det3[step], det3[step + 1] } };
 
                /* Check the mask - why not just check the mask at the center of the wavelet? */
                if (!mask_sum.empty())
                {
                    const int* mask_ptr = &mask_sum.at<int>(sum_i, sum_j);
                    float mval = calcHaarPattern(mask_ptr, &Dm, 1);
                    if (mval < 0.5)
                        continue;
                }
 
                /* 检测val0，是否在N9里极大值，？？为什么不检测极小值呢*/
                if (val0 > N9[0][0] && val0 > N9[0][1] && val0 > N9[0][2] &&
                    val0 > N9[0][3] && val0 > N9[0][4] && val0 > N9[0][5] &&
                    val0 > N9[0][6] && val0 > N9[0][7] && val0 > N9[0][8] &&
                    val0 > N9[1][0] && val0 > N9[1][1] && val0 > N9[1][2] &&
                    val0 > N9[1][3] && val0 > N9[1][5] &&
                    val0 > N9[1][6] && val0 > N9[1][7] && val0 > N9[1][8] &&
                    val0 > N9[2][0] && val0 > N9[2][1] && val0 > N9[2][2] &&
                    val0 > N9[2][3] && val0 > N9[2][4] && val0 > N9[2][5] &&
                    val0 > N9[2][6] && val0 > N9[2][7] && val0 > N9[2][8])
                {
                    /* Calculate the wavelet center coordinates for the maxima */
                    float center_i = sum_i + (size - 1)*0.5f;
                    float center_j = sum_j + (size - 1)*0.5f;
 
                    KeyPoint kpt(center_j, center_i, (float)sizes[layer],
                        -1, val0, octave, CV_SIGN(trace_ptr[j]));
 
                    /* 局部极大值插值，用Hessian，类似于SIFT里的插值，里面没有迭代5次，只进行了一次查找，why?  */
                    int ds = size - sizes[layer - 1];
                    int interp_ok = interpolateKeypoint(N9, sampleStep, sampleStep, ds, kpt);
 
                    /* Sometimes the interpolation step gives a negative size etc. */
                    if (interp_ok)
                    {
                        /*printf( "KeyPoint %f %f %d\n", point.pt.x, point.pt.y, point.size );*/
                        keypoints.push_back(kpt);
                    }
                }
            }
        }
    }
}

4 特征点描述子生成

特征点描述子的生成这一部分的代码主要是通过SURFInvoker这个类来实现。在主流程中，通过一个parallel_for_()函数来并发计算。

struct SURFInvoker
{
    enum{ORI_RADIUS = 6, ORI_WIN = 60, PATCH_SZ = 20};
    // Parameters
    const Mat* img;
    const Mat* sum;
    vector<KeyPoint>* keypoints;
    Mat* descriptors;
    bool extended;
    bool upright;
 
    // Pre-calculated values
    int nOriSamples;
    vector<Point> apt; // 特征点周围用于描述方向的邻域的点
    vector<float> aptw; // 描述 方向时的 高斯 权
    vector<float> DW;
 
 
    SURFInvoker(const Mat& _img, const Mat& _sum,
        vector<KeyPoint>& _keypoints, Mat& _descriptors,
        bool _extended, bool _upright)
    {
        keypoints = &_keypoints;
        descriptors = &_descriptors;
        img = &_img;
        sum = &_sum;
        extended = _extended;
        upright = _upright;
 
        // 用于描述特征点的 方向的 邻域大小： 12*sigma+1 (sigma =1.2) 因为高斯加权的核的参数为2sigma
        // nOriSampleBound为 矩形框内点的个数
        const int nOriSampleBound = (2 * ORI_RADIUS + 1)*(2 * ORI_RADIUS + 1); // 这里把s近似为1 ORI_DADIUS = 6s
 
        // 分配大小 
        apt.resize(nOriSampleBound);
        aptw.resize(nOriSampleBound);
        DW.resize(PATCH_SZ*PATCH_SZ); // PATHC_SZ为特征描述子的 区域大小 20s(s 这里初始为1了)
 
        /* 计算特征点方向用的 高斯分布 权值与坐标 */
        Mat G_ori = getGaussianKernel(2 * ORI_RADIUS + 1, SURF_ORI_SIGMA, CV_32F); // SURF_ORI_SIGMA = 1.2 *2 =2.5
        nOriSamples = 0;
        for (int i = -ORI_RADIUS; i <= ORI_RADIUS; i++)
        {
            for (int j = -ORI_RADIUS; j <= ORI_RADIUS; j++)
            {
                if (i*i + j*j <= ORI_RADIUS*ORI_RADIUS) // 限制在圆形区域内
                {
                    apt[nOriSamples] = cvPoint(i, j);
                    // 下面这里有个坐标转换，因为i,j都是从-ORI_RADIUS开始的。
                    aptw[nOriSamples++] = G_ori.at<float>(i + ORI_RADIUS, 0) * G_ori.at<float>(j + ORI_RADIUS, 0);
                }
            }
        }
        CV_Assert(nOriSamples <= nOriSampleBound); // nOriSamples为圆形区域内的点，nOriSampleBound是正方形区域的点
 
        /* 用于特征点描述子的高斯 权值 */
        Mat G_desc = getGaussianKernel(PATCH_SZ, SURF_DESC_SIGMA, CV_32F); // 用于生成特征描述子的 高斯加权 sigma = 3.3s (s初取1)
        for (int i = 0; i < PATCH_SZ; i++)
        {
            for (int j = 0; j < PATCH_SZ; j++)
                DW[i*PATCH_SZ + j] = G_desc.at<float>(i, 0) * G_desc.at<float>(j, 0);
        }
 
        /* x与y方向上的 Harr小波,参数为4s */
        const int NX = 2, NY = 2;
        const int dx_s[NX][5] = { { 0, 0, 2, 4, -1 }, { 2, 0, 4, 4, 1 } };
        const int dy_s[NY][5] = { { 0, 0, 4, 2, 1 }, { 0, 2, 4, 4, -1 } };
 
        float X[nOriSampleBound], Y[nOriSampleBound], angle[nOriSampleBound]; // 用于计算特生点主方向
        uchar PATCH[PATCH_SZ + 1][PATCH_SZ + 1];
        float DX[PATCH_SZ][PATCH_SZ], DY[PATCH_SZ][PATCH_SZ]; // 20s * 20s区域的 梯度值
        CvMat matX = cvMat(1, nOriSampleBound, CV_32F, X);
        CvMat matY = cvMat(1, nOriSampleBound, CV_32F, Y);
        CvMat _angle = cvMat(1, nOriSampleBound, CV_32F, angle);
        Mat _patch(PATCH_SZ + 1, PATCH_SZ + 1, CV_8U, PATCH);
 
        int dsize = extended ? 128 : 64;
 
        int k, k1 = 0, k2 = (int)(*keypoints).size();// k2为Harr小波的 模板尺寸
        float maxSize = 0;
        for (k = k1; k < k2; k++)
        {
            maxSize = std::max(maxSize, (*keypoints)[k].size);
        }
        // maxSize*1.2/9 表示最大的尺度 s
        int imaxSize = std::max(cvCeil((PATCH_SZ + 1)*maxSize*1.2f / 9.0f), 1);
        Ptr<CvMat> winbuf = cvCreateMat(1, imaxSize*imaxSize, CV_8U);
        for (k = k1; k < k2; k++)
        {
            int i, j, kk, nangle;
            float* vec;
            SurfHF dx_t[NX], dy_t[NY];
            KeyPoint& kp = (*keypoints)[k];
            float size = kp.size;
            Point2f center = kp.pt;
            /* s是当前层的尺度参数 1.2是第一层的参数，9是第一层的模板大小*/
            float s = size*1.2f / 9.0f;
            /* grad_wav_size是 harr梯度模板的大小 边长为 4s */
            int grad_wav_size = 2 * cvRound(2 * s);
            if (sum->rows < grad_wav_size || sum->cols < grad_wav_size)
            {
                /* when grad_wav_size is too big,
                * the sampling of gradient will be meaningless
                * mark keypoint for deletion. */
                kp.size = -1;
                continue;
            }
 
            float descriptor_dir = 360.f - 90.f;
            if (upright == 0)
            {
                // 这一步 是计算梯度值，先将harr模板放大，再根据积分图计算，与前面求D_x，D_y一致类似
                resizeHaarPattern(dx_s, dx_t, NX, 4, grad_wav_size, sum->cols);
                resizeHaarPattern(dy_s, dy_t, NY, 4, grad_wav_size, sum->cols);
                for (kk = 0, nangle = 0; kk < nOriSamples; kk++)
                {
                    int x = cvRound(center.x + apt[kk].x*s - (float)(grad_wav_size - 1) / 2);
                    int y = cvRound(center.y + apt[kk].y*s - (float)(grad_wav_size - 1) / 2);
                    if (y < 0 || y >= sum->rows - grad_wav_size ||
                        x < 0 || x >= sum->cols - grad_wav_size)
                        continue;
                    const int* ptr = &sum->at<int>(y, x);
                    float vx = calcHaarPattern(ptr, dx_t, 2);
                    float vy = calcHaarPattern(ptr, dy_t, 2);
                    X[nangle] = vx*aptw[kk];
                    Y[nangle] = vy*aptw[kk];
                    nangle++;
                }
                if (nangle == 0)
                {
                    // No gradient could be sampled because the keypoint is too
                    // near too one or more of the sides of the image. As we
                    // therefore cannot find a dominant direction, we skip this
                    // keypoint and mark it for later deletion from the sequence.
                    kp.size = -1;
                    continue;
                }
                matX.cols = matY.cols = _angle.cols = nangle;
                // 计算邻域内每个点的 梯度角度
                cvCartToPolar(&matX, &matY, 0, &_angle, 1);
 
                float bestx = 0, besty = 0, descriptor_mod = 0;
                for (i = 0; i < 360; i += SURF_ORI_SEARCH_INC) // SURF_ORI_SEARCH_INC 为扇形区域扫描的步长
                {
                    float sumx = 0, sumy = 0, temp_mod;
                    for (j = 0; j < nangle; j++)
                    {
                        // d是 分析到的那个点与 现在主方向的偏度
                        int d = std::abs(cvRound(angle[j]) - i);
                        if (d < ORI_WIN / 2 || d > 360 - ORI_WIN / 2)
                        {
                            sumx += X[j];
                            sumy += Y[j];
                        }
                    }
                    temp_mod = sumx*sumx + sumy*sumy;
                    // descriptor_mod 是最大峰值
                    if (temp_mod > descriptor_mod)
                    {
                        descriptor_mod = temp_mod;
                        bestx = sumx;
                        besty = sumy;
                    }
                }
                descriptor_dir = fastAtan2(-besty, bestx);
            }
            kp.angle = descriptor_dir;
            if (!descriptors || !descriptors->data)
                continue;
 
            /* 用特征点周围20*s为边长的邻域 计算特征描述子 */
            int win_size = (int)((PATCH_SZ + 1)*s);
            CV_Assert(winbuf->cols >= win_size*win_size);
            Mat win(win_size, win_size, CV_8U, winbuf->data.ptr);
 
            if (!upright)
            {
                descriptor_dir *= (float)(CV_PI / 180); // 特征点的主方向 弧度值
                float sin_dir = -std::sin(descriptor_dir); //  - sin dir
                float cos_dir = std::cos(descriptor_dir);
 
                float win_offset = -(float)(win_size - 1) / 2;
                float start_x = center.x + win_offset*cos_dir + win_offset*sin_dir;
                float start_y = center.y - win_offset*sin_dir + win_offset*cos_dir;
                uchar* WIN = win.data;
 
                int ncols1 = img->cols - 1, nrows1 = img->rows - 1;
                size_t imgstep = img->step;
                for (i = 0; i < win_size; i++, start_x += sin_dir, start_y += cos_dir)
                {
                    double pixel_x = start_x;
                    double pixel_y = start_y;
                    for (j = 0; j < win_size; j++, pixel_x += cos_dir, pixel_y -= sin_dir)
                    {
                        int ix = cvFloor(pixel_x), iy = cvFloor(pixel_y);
                        if ((unsigned)ix < (unsigned)ncols1 &&
                            (unsigned)iy < (unsigned)nrows1)
                        {
                            float a = (float)(pixel_x - ix), b = (float)(pixel_y - iy);
                            const uchar* imgptr = &img->at<uchar>(iy, ix);
                            WIN[i*win_size + j] = (uchar)
                                cvRound(imgptr[0] * (1.f - a)*(1.f - b) +
                                imgptr[1] * a*(1.f - b) +
                                imgptr[imgstep] * (1.f - a)*b +
                                imgptr[imgstep + 1] * a*b);
                        }
                        else
                        {
                            int x = std::min(std::max(cvRound(pixel_x), 0), ncols1);
                            int y = std::min(std::max(cvRound(pixel_y), 0), nrows1);
                            WIN[i*win_size + j] = img->at<uchar>(y, x);
                        }
                    }
                }
            }
            else
            {
 
                float win_offset = -(float)(win_size - 1) / 2;
                int start_x = cvRound(center.x + win_offset);
                int start_y = cvRound(center.y - win_offset);
                uchar* WIN = win.data;
                for (i = 0; i < win_size; i++, start_x++)
                {
                    int pixel_x = start_x;
                    int pixel_y = start_y;
                    for (j = 0; j < win_size; j++, pixel_y--)
                    {
                        int x = MAX(pixel_x, 0);
                        int y = MAX(pixel_y, 0);
                        x = MIN(x, img->cols - 1);
                        y = MIN(y, img->rows - 1);
                        WIN[i*win_size + j] = img->at<uchar>(y, x);
                    }
                }
            }
            // Scale the window to size PATCH_SZ so each pixel's size is s. This
            // makes calculating the gradients with wavelets of size 2s easy
            resize(win, _patch, _patch.size(), 0, 0, INTER_AREA);
 
            // Calculate gradients in x and y with wavelets of size 2s
            for (i = 0; i < PATCH_SZ; i++)
            for (j = 0; j < PATCH_SZ; j++)
            {
                float dw = DW[i*PATCH_SZ + j]; // 高斯加权系数
                float vx = (PATCH[i][j + 1] - PATCH[i][j] + PATCH[i + 1][j + 1] - PATCH[i + 1][j])*dw;
                float vy = (PATCH[i + 1][j] - PATCH[i][j] + PATCH[i + 1][j + 1] - PATCH[i][j + 1])*dw;
                DX[i][j] = vx;
                DY[i][j] = vy;
            }
 
            // Construct the descriptor
            vec = descriptors->ptr<float>(k);
            for (kk = 0; kk < dsize; kk++)
                vec[kk] = 0;
            double square_mag = 0;
            if (extended)
            {
                // 128维描述子，考虑dx与dy的正负号
                for (i = 0; i < 4; i++)
                for (j = 0; j < 4; j++)
                {
                    // 每个方块内是一个5s * 5s的区域，每个方法由8个特征描述
                    for (int y = i * 5; y < i * 5 + 5; y++)
                    {
                        for (int x = j * 5; x < j * 5 + 5; x++)
                        {
                            float tx = DX[y][x], ty = DY[y][x];
                            if (ty >= 0)
                            {
                                vec[0] += tx;
                                vec[1] += (float)fabs(tx);
                            }
                            else {
                                vec[2] += tx;
                                vec[3] += (float)fabs(tx);
                            }
                            if (tx >= 0)
                            {
                                vec[4] += ty;
                                vec[5] += (float)fabs(ty);
                            }
                            else {
                                vec[6] += ty;
                                vec[7] += (float)fabs(ty);
                            }
                        }
                    }
                    for (kk = 0; kk < 8; kk++)
                        square_mag += vec[kk] * vec[kk];
                    vec += 8;
                }
            }
            else
            {
                // 64位描述子
                for (i = 0; i < 4; i++)
                for (j = 0; j < 4; j++)
                {
                    for (int y = i * 5; y < i * 5 + 5; y++)
                    {
                        for (int x = j * 5; x < j * 5 + 5; x++)
                        {
                            float tx = DX[y][x], ty = DY[y][x];
                            vec[0] += tx; vec[1] += ty;
                            vec[2] += (float)fabs(tx); vec[3] += (float)fabs(ty);
                        }
                    }
                    for (kk = 0; kk < 4; kk++)
                        square_mag += vec[kk] * vec[kk];
                    vec += 4;
                }
            }
            // 归一化 描述子 以满足 光照不变性
            vec = descriptors->ptr<float>(k);
            float scale = (float)(1. / (sqrt(square_mag) + DBL_EPSILON));
            for (kk = 0; kk < dsize; kk++)
                vec[kk] *= scale;
        }
    }
};

from：SURF算法与源码分析、上 - ☆Ronny丶 - 博客园

from：SURF算法与源码分析、下 - ☆Ronny丶 - 博客园